La catoptrice : une courbe presque oubliée

On appelle catoptrice (du Grec \(\kappa \alpha \tau o\pi \tau \rho o \nu \) – miroir) ⁷J’ai traduit ce terme de l’Anglais Catoptrix. Le mot Catoptrique qui serait peut-être l’appellation française de cette courbe désigne la partie de l’Optique qui traite de la refléxion de rayons de lumière, des lois que suit cette réflexion et des phénomènes qui en résultent par rapport à la vision. Dans ce sens on peut, par exemple, jeter un coup d’œil sur cette page ou encore sur cette autre. une courbe C qui jouit de la propriété qu’il existe un point F intérieur à C tel que si un rayon de lumière passant par ce point est réfléchi en M puis en N sur cette courbe alors ce rayon passe de nouveau par F.

Le problème de la détermination des catoptrices, posé par Euler en 1745 dans Nova Acta Eruditorum, est peut-être le plus intéressant parmi une collection de problèmes étudiés surtout par Euler et probablement nommés par lui « Problèmes réciproques » ⁸Lorsqu’on connait un type particulier de courbes satisfaisant une propriété bien déterminée, le « Problème réciproque » pour cette propriété est de trouver d’autres courbes satisfaisant cette propriété. Les ellipses, vu leur propriété optique ⁹Quand un rayon de lumière part d’un foyer (ou passe par un foyer) d’un miroir elliptique, le rayon réfléchi passe par l’autre foyer., sont des catoptrices (relativement à un foyer) (fig.1), mais Euler voulait connaitre toutes les autres. Il ne laisse pas beaucoup de temps à ses collègues pour travailler sur ce problème puisque l’année suivante et dans le même journal, il présente sa « Solution au problème de la catoptrice ». Sa première méthode appliquée conduit à des équations différentielles pour les courbes solutions. La résolution de ces équations n’arrive que deux ans plus tard. L’autre méthode utilise la notion de lieu géométrique : une catoptrice est définie comme le « lieu » déterminé par le mouvement d’un point sur une autre courbe initiale appelée « courbe source », notion utilisée également dans les autres problèmes réciproques déjà étudiés comme celui des « trajectoires réciproques » ¹⁰Voir la référence supra, p. 304..

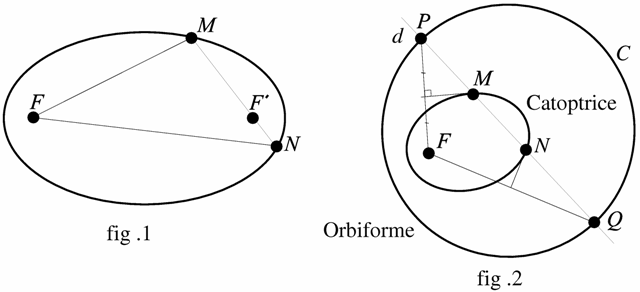
De nos jours presque personne ne connaît la catoptrice, mais presque tout mathématicien a entendu parler des « Courbes de Reuleaux » ¹¹Voir cet  article de Serge Cantat. Voir aussi cette page., « Courbes à diamètre (ou largeur) constant (e) » ou « Orbiformes » ¹² Orbiforme : du latin orbis «cercle» et forme. (Euler) dont l’étude rigoureuse semble avoir été faite par ce grand mathématicien dans  » Sur les courbes triangulaires » publié en 1778.

L’intérêt porté par Euler aux Orbiformes consiste en ce que ceux-ci permettent bien une construction facile des catoptrices, c’est-à-dire qu’ils constituent les courbes sources pour ces dernières, comme nous allons le voir tout de suite.

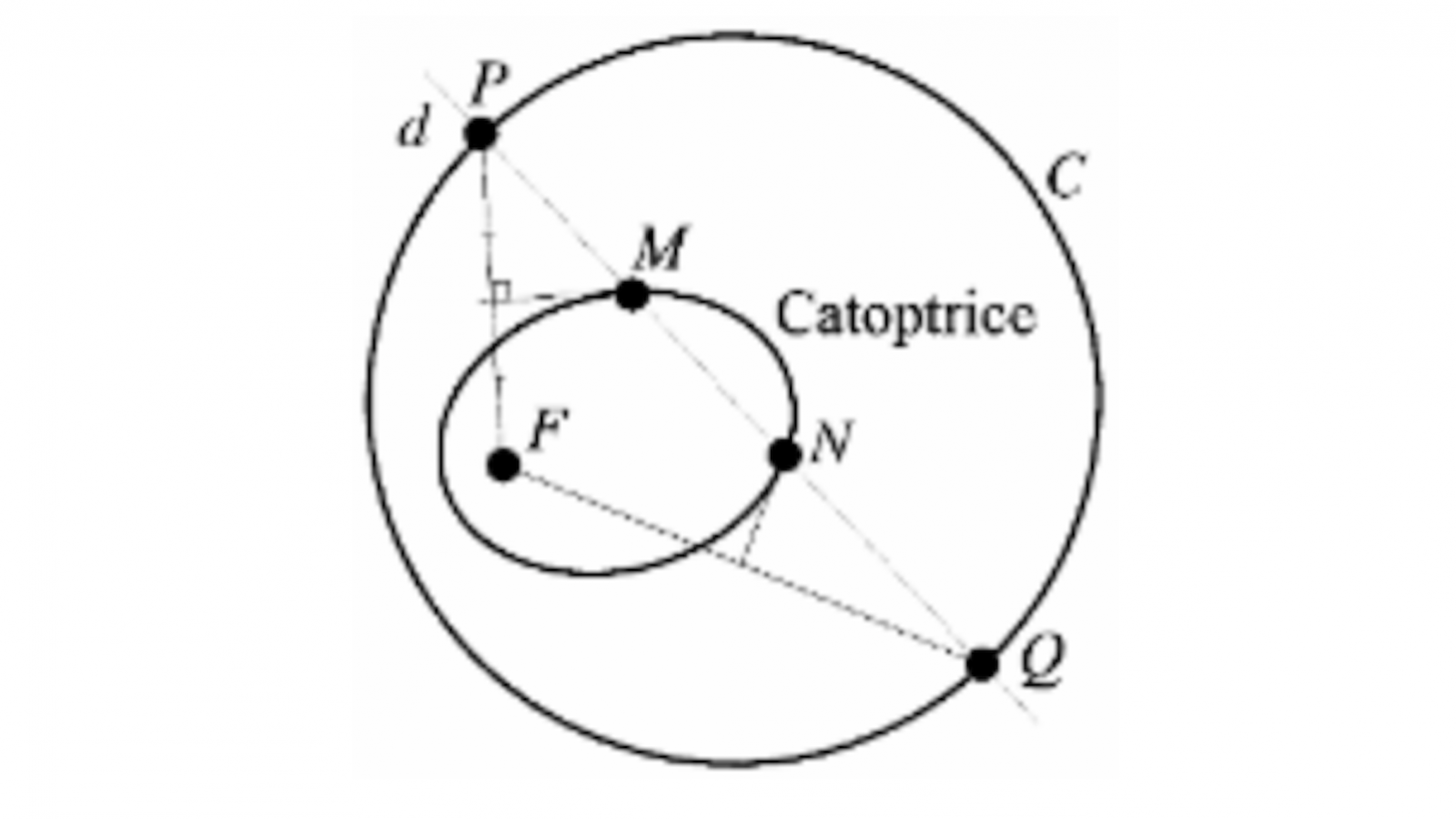
Soient C une courbe de diamètre constant (orbiforme) et F un point intérieur à cette courbe. Soient P un point de C, d la normale en P et Q le deuxième point commun à C et d. La droite d est aussi la normale à C en Q et le segment [PQ] a une longueur constante. Soit M (resp. N) le point de rencontre de la médiatrice de [FP] (resp. [FQ]) avec [PQ].

L’ensemble décrit par M lorsque P décrit C est une catoptrice, où le segment [FM] est réfléchi sur [MN] qui à son tour est renvoyé vers F. (fig.2) Si C est un cercle, la catoptrice est l’ellipse de foyers F et le centre du cercle.

 

Référence

The Geometry of Leonhard Euler by Homer White in Leonhard Euler : Life, Work and Legacy, Robert E. Bradley and C. Edward Sandifer (Editors). Elsevier 2007. p. 308-311.