La musique comme une langue

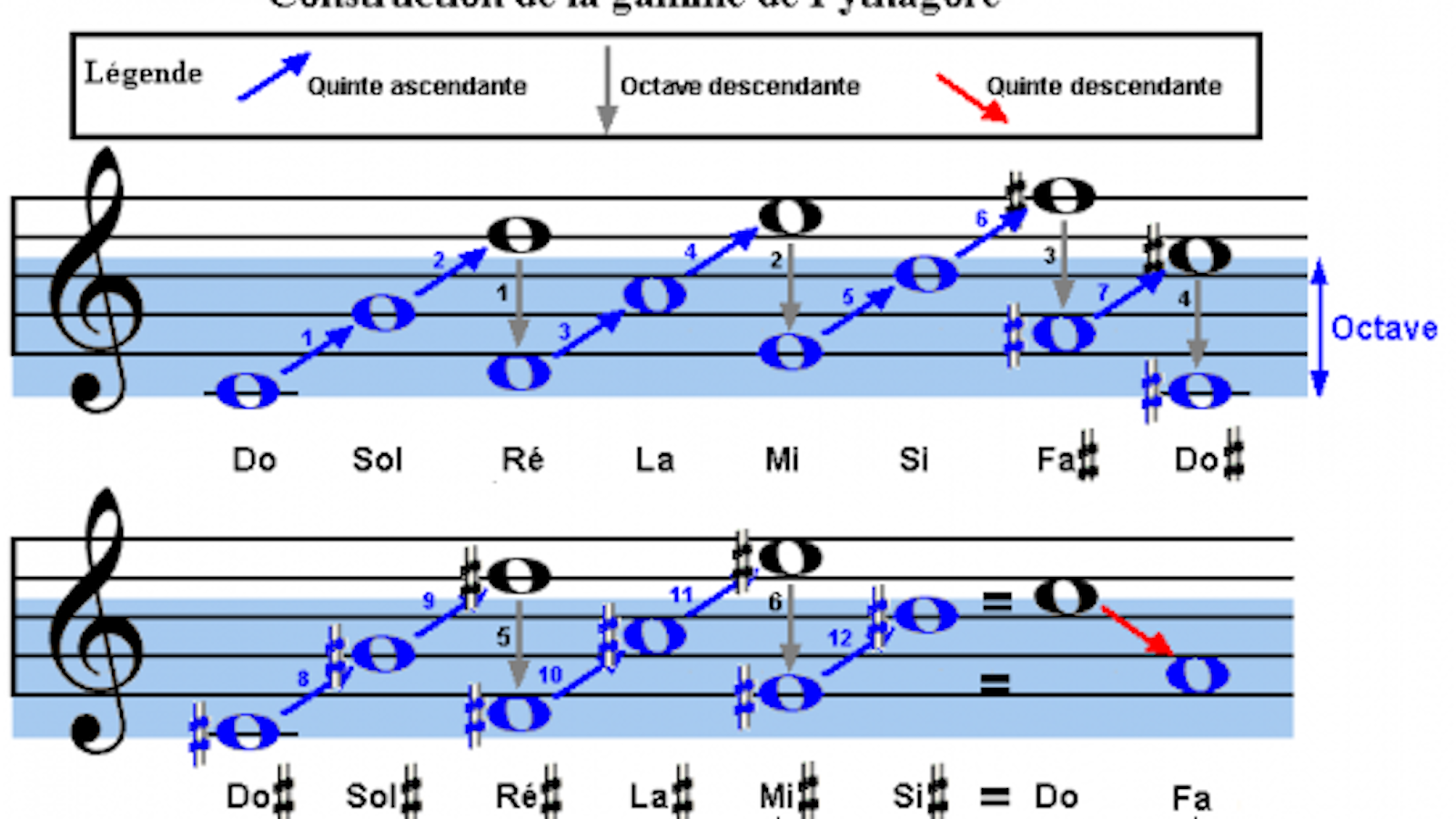
L’histoire de l’analyse musicale en tant que science est un bon exemple pour voir les liens existants entre mathématiques et langages. En effet, de Pythagore à Euler et encore aujourd’hui, les liens entre les mathématiques et la musique sont très forts. À l’époque antique, la musique était partie intégrante des arts mathématiques appelés quadrivium avec l’arithmétique, la géométrie et l’astronomie. Pythagore avait créé une gamme musicale qui a survécu jusqu’à la fin du Moyen-Âge, à partir d’une méthode purement arithmétique en effectuant des fractions rationnelles d’une corde. L’arithmétique a également été utilisée pour effectuer des études musicologiques afin d’expliquer mathématiquement les principes inhérents au concept de tonalité en musique. Euler, en 1739, propose une structure en graphe avec une visualisation des quintes justes et des tierces majeures et mineures, permettant une représentation mathématique de l’intonation juste. Tout mouvement dans cette intonation pouvant être considéré comme un déplacement dans ce graphe. Aujourd’hui, les outils mathématiques algébriques de théorie des groupes ou géométriques sont encore utilisés pour la musique, avec des adaptations aux nouveaux styles musicaux, de la musique atonale à la pop.

Au vingtième siècle, il n’a pas fallu attendre longtemps pour que les outils linguistiques de caractérisation des langages formels, introduits par Noam Chomsky notamment, soient utilisés pour l’analyse musicale. Nous parlons en effet dans la vie courante de langage musical, mais nous pouvons également analyser la musique comme un langage formel. Lerdahl et Jackendoff ont proposé une théorie générative de la musique tonale dans le but de trouver des grammaires musicales pouvant expliquer scientifiquement les volontés d’un compositeur. Cette théorie propose des méthodes d’analyse de la structure musicale, du rythme et de l’harmonie.

En 1980, Morando proposait une approche statistique de l’analyse musicale. Considérant une partition musicale comme un ensemble de données séquentielles, il construit et analyse des tableaux de correspondance et montre notamment que l’analyse statistique retrouve rapidement des règles classiques. Conklin utilise des outils issus de la modélisation statistique du langage, il propose quant à lui une approche statistique pour la génération de musique. Pour ce faire, il considère un ensemble de vues de la surface musicale modélisant chacune un phénomène musical particulier. Il crée alors un modèle prédictif basé sur des techniques d’apprentissage automatique.

Les outils informatiques permettent d’implémenter ces différents outils mathématiques et linguistiques. Les ordinateurs sont alors capables de faire des analyses musicologiques, de composer de la musique respectant un certain style, et même d’improviser de la musique en interaction avec un improvisateur humain. Aujourd’hui, avec la possibilité d’utiliser de grands corpus musicaux et l’accessibilité des processeurs graphiques, l’application de nouveaux modèles d’apprentissage automatique comme les réseaux de neurones artificiels étend ce champ de recherche.