Parmi les nombreuses quadratrices que connaît le monde des courbes, c’est-à-dire les courbes planes qui permettent une quadrature du cercle, on trouve la quadratrice d’Abdank-Abakanowicz qu’on peut construire à l’aide d’un instrument d’intégration : l’intégraphe d’Abdank-Abakanowicz.
Naissance des quadratrices
Le lecteur des Éléments d’Euclide peut constater que toutes les constructions géométriques étudiées dans ces livres s’effectuent à la règle et au compas. Même avant Euclide les mathématiciens grecs se sont intéressés à ces deux instruments. La notion de constructibilité (qui, désormais, sous-entendra à la règle et au compas) d’un nombre réel ou plus généralement complexe a même conduit au corps des nombres constructibles. Cependant, dès le cinquième siècle avant Jésus-Christ, des problèmes insolubles à l’aide de la règle et du compas sont apparus. Les plus réputés de ces problèmes sont à l’unanimité :
1- La quadrature du cercle, c’est-à-dire la construction, à la règle et au compas, (du côté) d’un carré ayant la même aire qu’un disque donné.
2- La duplication du cube qui consiste elle, à construire, à la règle et au compas, (l’arête d’) un cube ayant un volume double de celui d’un cube donné.
3- La trisection de l’angle qui revient à construire, à la règle et au compas, les demi-droites qui divisent un angle donné en trois angles de même mesure.
L’impossibilité de la quadrature du cercle, i.e. l’impossibilité de construire à la règle et au compas un segment de longueur \(\sqrt\pi\) (ou de longueur \(\pi\)) connaissant le nombre \(1\), ne fut prouvée qu’en 1882 par Lindemann (voir Encart 1).Pour la duplication du cube qui se ramène à la construction, à la règle et au compas, d’un segment de longueur \(\sqrt[3]{2}\), on a montré que cette construction est également impossible (voir Encart 2).
La trisection de l’angle à la règle et au compas n’est faisable que dans certains cas (voir Encart 3).
Une courbe qui permet de résoudre le problème de la quadrature du cercle, en d’autres termes une courbe qui contient un point dont l’abscisse ou l’ordonnée est égale à \(\pi\) ou à l’un de ses multiples ou sous-multiples s’appelle une quadratrice.
On attribue à Hippias d’Élis l’introduction en Mathématique de la première courbe qui vient juste après la droite et le cercle. Proclus et d’autres commentateurs lui attribuent la courbe nommée depuis, trisectrice (courbe permettant la trisection d’un angle) ou quadratrice d’Hippias. En fait c’est Dinostrate qui remarqua le premier que la trisectrice d’Hippias est une quadratrice. Son frère Menechme résolut le problème de la duplication du cube.
L’ancêtre des quadratrices : la quadratrice d’Hippias, alias la quadratrice de Dinostrate
Comme cette courbe est l’ancêtre des quadratrices, il serait plus juste de lui rendre un peu d’hommage.
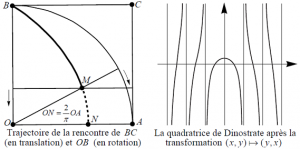
La quadratrice de Dinostrate est la trajectoire d’un point ayant une vitesse angulaire constante par rapport à un point fixe et une composante de son vecteur vitesse constante. C’est aussi la trajectoire de la rencontre d’une droite en translation uniforme et d’une droite en rotation uniforme.
Une équation en coordonnées polaires, lorsque le point fixe est \(O\) et la composante constante du vecteur vitesse est celle suivant \(Ox\) est
\[\rho = \frac{{2a}}{\pi }\frac{\theta }{{\sin \theta }}\]
où \(a\) est un réel non nul.
En coordonnées cartésiennes elle est définie par le paramétrage
\[t \mapsto \left( {\frac{{2at}}{\pi }\cot t,\frac{{2at}}{\pi }} \right)\]
Notons que si l’on considère la paramétrisation complexe
\[z(\theta ) = a\frac{\theta }{{\sin \theta }}{e^{i\theta }}\] on a
\[\frac{{z(\theta ) + \left| {z(\theta )} \right|}}{2} = z\left( {\frac{\theta }{2}} \right) ;\]
l’image de la suite \(({u_n})\) définie par \({u_0} = {\rho _0}{e^{i{\theta _0}}}\) et par la relation de récurrence \(2{u_{n + 1}} = {u_n} + \left| {{u_n}} \right|\) est incluse dans la quadratrice définie par \[\rho = {\rho _0}\frac{{\sin {\theta _0}}}{{{\theta _0}}}\frac{\theta }{{\sin \theta }}\] et sa limite est \[\rho = {\rho _0}\frac{{\sin {\theta _0}}}{{{\theta _0}}}.\]
Pour \(a=1\) on a \[\mathop {\lim }\limits_{t \to 0} \left( {x(t),y(t)} \right) = \left( {\frac{2}{\pi },0} \right),\] ce qui permet la construction d’un segment de longueur \(\frac{\pi }{2}\)( cf note 1), puis la quadrature du cercle (cf note 2)
Cette courbe a été inventée pour servir de trisectrice comme on l’a signalé ci-dessus, mais, et pour la bonne chance des géométries, elle a aussi rendu service pour la quadrature du cercle, et mieux encore, joué le rôle de \(n\)-sectrice.
Pour un peu plus de détail, jeter un coup d’œil ici, ou encore là.
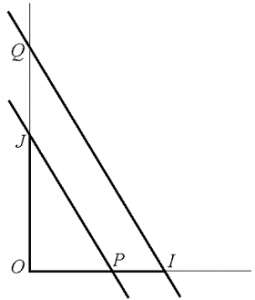
Note 1 : On considère dans un repère orthonormal les points \(I(1,0)\), \(J(0,1)\) et \(P(\frac{2}{\pi },0)\). La parallèle à \((PJ)\) menée de \(I\) rencontre l’axe des ordonnées en \(Q\) tel que \(\frac{{OQ}}{{OJ}} = \frac{{OI}}{{OP}}\).(d’après Thalès). D’où \[OQ = \frac{1}{{OP}} = \frac{\pi }{2}.\]
.
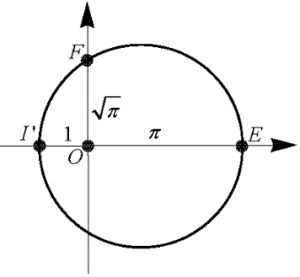
Note 2 : On construit le cercle de diamètre \(I’E\) où \(I’\) est le point de coordonnées \((-1,0)\) et \(E\) de coordonnées \((\pi, 0)\). Ce cercle rencontre l’axe des ordonnées en le point d’ordonnée positive \(F\), et on a \(OF=\sqrt{\pi}\) (qui vient du fait que l’on a \(OF^2=OI’.OE\) par la propriété de la hauteur relative à l’hypoténuse dans un triangle rectangle, ou de la puissance de \(O\) par rapport au cercle.), i.e. le côté d’un carré dont l’aire est celle d’un disque de rayon 1.
.
Aperçu sur les intégraphes
Les ancêtres des intégraphes sont les intégrateurs mécaniques, instruments dont l’origine date du début du 19e siècle et qui effectuent, dans certaines conditions et par des moyens purement mécaniques, la sommation d’une série infinie de grandeurs infiniment petites. Ces grandeurs peuvent être les éléments de l’aire d’une surface bordée par une courbe, ou d’une grandeur complexe quelconque, un travail mécanique, une chaleur, une énergie électrique, etc.
Dans tous ces instruments on se borne à rechercher le résultat d’une intégration et « presque tous » les problèmes qui se présentent dans les sciences appliquées peuvent se ramener à celui du calcul d’une aire.
Ces appareils d’intégration se ramènent à deux principes de base qui correspondent aux deux aspects de l’intégrale ; soit on fait une quadrature, i.e. on évalue l’aire sous une courbe en la décomposant en une somme infinie de petites figures élémentaires, soit on résout un problème inverse des tangentes, i.e. on construit une courbe dont le coefficient directeur des tangentes est donné (primitive). Les intégrateurs du premier type, qui servent principalement à mesurer l’aire d’une surface délimitée par une courbe fermée, sont appelés « planimètres ». Les intégrateurs du second type, quant à eux, sont appelés « intégraphes » dans la mesure où ils permettent de tracer d’une façon continue une courbe intégrale d’une courbe donnée.
Les intégraphes sont des intégrateurs qui non seulement effectuent la somme totale des éléments, mais donnent encore, sous forme de tracé graphique d’une courbe qui n’est autre qu’une courbe intégrale, la loi complète qui gouverne la sommation. Ils peuvent intégrer (résoudre) des équations différentielles élémentaires.
Quadratrice et intégraphe d’Abdank-Abakanowicz
Il est à remarquer que le travail de Lindemann sur la transcendance du nombre \(\pi\) a montré qu’il n’est pas seulement impossible de « construire » ce nombre à l’aide de la règle et du compas, mais qu’il n’existe même pas une courbe de degré supérieur définie par une équation algébrique à coefficients entiers pour laquelle \(\pi\) est l’ordonnée correspondant à une valeur rationnelle de l’abscisse. Il en résulte qu’une construction de \(\pi\) ne peut être réalisée qu’à l’aide d’une courbe transcendante, et pour ce faire on doit utiliser, excepté la règle et le compas, un instrument ‘transcendantal » qui tracera la courbe par un mouvement continu.
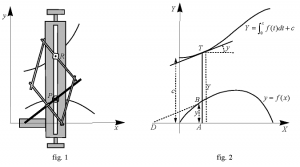
Le premier tel instrument est l’intégraphe (fig. 1) inventé et décrit par l’ingénieur Abdank Abakanowicz et construit par Coradi de Zürich.
Nous avons donné le nom d’intégraphes à ce nouveau genre d’intégrateurs, que nous croyons pouvoir affirmer avoir été les premiers à construire. B. Abdank-Abakanowicz, Référence 1, p. vi. 2Le mathématicien français Gustave Gaspard Coriolis est le premier à décrire en 1836 le principe fondamental sur lequel est basé l’intégraphe mécanique, dans le Journal de Mathématiques Pures et Appliquées ou le Journal de Liouville, Paris, 1836.
Cet instrument permet de construire la {courbe intégrale} définie par l’équation
\[Y = F(x) = \int_a^x {f(t)dt} \]
connaissant la {courbe différentielle} définie par l’équation
\[y=f(x).\]
Lorsqu’on fait bouger le système articulé de l’intégraphe de telle sorte que la pointe directrice \(P\) décrit la courbe différentielle, la {pointe traçante} \(R\) décrit alors la courbe intégrale (fig. 2).
On décrit succinctement ci-dessous le principe mathématique sur lequel se base l’intégraphe.
Soit \(B\) un point quelconque de la courbe définie par l’équation \(y=f(x)\). On construit le triangle rectangle de sommets \(B(x,y)\), \(A(x,0)\) et \(D(x-1,0)\). La tangente de l’angle \(\widehat {ADB}\), i.e. le coefficient directeur de la droite \((DB)\) égale \(y\). Donc \((BD)\) est parallèle à la tangente à la courbe intégrale au point \(T(X,Y)\) correspondant au point \(B(x,y)\).
.
Voici une autre description du principe de fonctionnement de l’intégraphe d’Abdank-Abakanowicz par Maurice d’Ocagne, dans son livre Calcul graphique et nomographie, Paris : O. Doin ; 2ème éd. revue et corrigée, 1914 ; 3ème éd., 1924. (cf. Référence 4 ) :
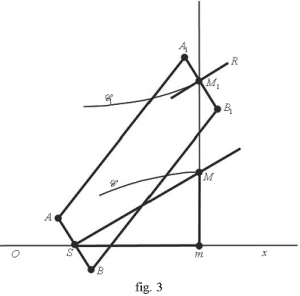
Une équerre mobile \(SmM\) glisse le long de l’axe des abscisses \(Ox\). Le côté \(Sm\) est pris pour unité de longueur. Le long du côté \(mM\) peuvent coulisser :
1) un pointeur \(M\), engagé en outre dans la coulisse d’une tige \(SM\) pivotant librement autour de \(S\) ;
2) le centre \(M_1\) d’une roulette \(R\) suffisamment pressée contre le plan horizontal sur lequel repose l’appareil.
L’axe \(A_1 B_1\) de la roulette \(R\) est relié par un parallélogramme articulé à une barre \(AB\) perpendiculaire à la tige \(SM\), de sorte que le plan de rotation de la roulette soit toujours parallèle à \(SM\). Lorsqu’on suit avec le pointeur \(M\) une courbe donnée \(\mathscr{C}\) d’équation \(y = ƒ(x)\), la roulette \(R\) enveloppe une courbe \(\mathscr{C}_1\) dont la tangente reste à chaque instant parallèle à \(SM\).
Comme \(Sm = 1\), la pente de cette tangente n’est autre que l’ordonnée \(mM = ƒ(x)\) de la courbe \(\mathscr{C}\). On trace ainsi une courbe \(\mathscr{C}_1\) dont la pente est constamment égale à \(ƒ(x)\) : c’est le graphe d’une primitive de \(ƒ\) (fig. 3).
.
Plus généralement, l’intégraphe d’Abdank-Abakanowicz permet de construire la courbe (intégrale) définie par la représentation paramétrique
\[X = x(t),Y = \int_0^t {ydx} = \int_0^t {y(u)x'(u)du} \]
associée à une courbe (différentielle) définie par la représentation paramétrique \[X = x(t),Y = y(t)\] donnée.
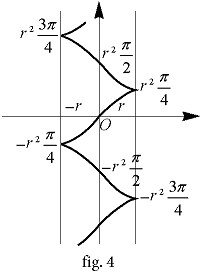
Pour construire \(\pi\), i.e. réaliser la quadrature du cercle, on considère (fig. 4) la courbe différentielle (cercle) définie par l’équation \[x^2+y^2=r^2,\] ou, d’une manière équivalente, par la représentation paramétrique \[x(t) = r\sin t, y(t) = r\cos t,\] et sa courbe intégrale définie par \[Y = \frac{{{r^2}}}{2}\arcsin \frac{x}{r} + \frac{x}{2}\sqrt {{r^2} – {x^2}}.\]
ou encore par la paramétrisation
\[x = r\sin t,y = \frac{{{r^2}}}{2}\left( {t + \sin t\cos t} \right).\].
.
Pour \(r=1\) la courbe contient les points de coordonnées \((1,\pi/4 )\), \((0,\pi /2 )\), \((0,\pi )\), etc., c’est-à-dire qu’elle permet la quadrature du cercle. C’est donc une quadratrice; on l’appelle la quadratrice d’Abdank-Abakanowicz ou encore intégrale de cercle.
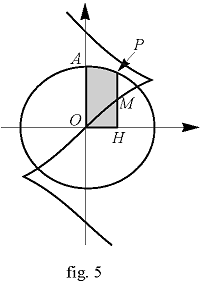
L’aire de la partie en grisé de la figure 5 est égale à \(HM.\)
En effet, on a :\(M\left( {r\sin t,\frac{{{r^2}}}{2}(t + \sin t\cos t)} \right)\), \(P(r\sin t, r\cos t)\), et en supposant \(0 < t < \frac{\pi }{2}\),
\[\tan \widehat {(\overrightarrow {OH} ,\overrightarrow {OP} )} = \frac{{\cos t}}{{\sin t}} = \tan \left( {\frac{\pi }{2} – t} \right).\]
L’aire du secteur circulaire \(OPA\) est
\[{{\cal A}_1}=\frac{{{r^2}t}}{2},\]
et celle du simplexe (triangle plein) \(OHP\) égale à
\[{{\cal A}_2}=\frac{{{r^2}\sin t\cos t}}{2}.\]
D’où le résultat mentionné, i.e.
\[{{\cal A}_1}+{{\cal A}_2}=HM\]
qui reste aussi valide pour \(t=0.\)
.
Références
1. Bruno Abdank-Abakanowicz, Les intégraphes. La courbe intégrale et ses applications, Gautier-Villars, 1886.
2. F. Klein, Leçons sur certaines questions de Géométrie élémentaire. Rédaction française par J. Griess. Paris, Librairie Nony et Cie, 1896.
3. Henry Lossier, L’Intégraphe Abdank Abakanowicz, Bulletin Technique de la Suisse Romande, No. 10, 20 Novembre 1900, p. 81-83.
4. Dominique Tournès, Du compas aux intégraphes : Les instruments du calcul graphique, REPERES – IREM. N° 50 – janvier 2003.
Encart 1
Le nombre \(\pi\) est transcendant, c’est-à-dire non algébrique : il n’existe pas de polynôme à coefficients rationnels dont \(\pi\) soit un zéro. En 1873, Hermite prouve que la base du logarithme népérien, le nombre \(e\), est transcendant. En 1882, Ferdinand von Lindemann généralise son raisonnement en un théorème (le théorème d’Hermite-Lindemann) qui stipule que, si \(\alpha\) est algébrique et non nul, alors le nombre \({e^\alpha}\) est transcendant. Or \({e^{i\pi }}\) n’est pas transcendant (puisqu’il est égal à \(\cos \pi + i\sin \pi =-1\)). Par contraposée (La contraposée d’une relation \(p \Rightarrow q\) est la relation \(\bar q \Rightarrow \bar p\), et on montre que ces deux relations sont équivalentes.), \(i\pi\) n’est pas algébrique donc \(\pi\) est transcendant, puisque \(i\) est algébrique (\(i^2+1=0\)). Enfin, d’après le théorème de Wantzel qui établit, en particulier, que tout nombre constructible (à l’aide de la règle et du compas) est algébrique, \(\pi\) n’est pas constructible.
Encart 2
Le nombre \(\sqrt[3]{2}\) n’est pas constructible en vertu du théorème de Wantzel, car, bien qu’algébrique (puisque c’est un zéro de \(X^3-2\)), son degré (trois) n’est pas une puissance de 2.
Encart 3
Sont «trisectables» les angles dont une mesure \(\alpha\) est telle que le nombre \(\cos(\alpha/3)\) est constructible à la règle et au compas à partir de \( \{0,1,\cos\alpha \}\) ; et ceci est possible si, et seulement si, le polynôme \({X^3} – 3X – 2\cos\alpha \) n’est pas irréductible sur le corps \(\bf Q(\cos \alpha )\) décrit par tous les nombres réels de la forme \(a + b\cos \alpha\) où \(a\) et \(b\) sont dans \(\bf Q\).
ÉCRIT PAR
Hamza Khelif
Enseignant de mathématique - El-Oued - Algérie
