La théorie des langages formels

Qu’est-ce qu’un langage formel ?

On étudie depuis longtemps la structure des langues : la grammaire de Pāṇini, qui décrit le sanscrit, date du cinquième siècle avant notre ère. Mais la grammaire classique est une science totalement séparée des mathématiques ; telle qu’elle est enseignée dans les écoles, elle a d’abord une fonction normative : donner le « bon usage » de la langue.

Une théorie mathématique des langages formels n’est apparue que dans les années 1950 ; l’une de ses questions de base est de reconnaître si une phrase appartient à une langue donnée. L’une des premières applications pratiques est de reconnaître si un programme informatique, vu comme un texte d’un langage de programmation (Java, Python, C…) est bien formé.

Les concepts de base sont trompeusement simples: on se donne un ensemble fini \(A\), l’alphabet, dont les éléments sont appelés lettres; dans les premiers exemples, l’alphabet n’a que deux lettres, notées \(0\) et \(1\) (c’est avec cela que marchent les ordinateurs, et on peut toujours s’y ramener). On définit un mot comme une suite finie de lettres (en réalité, il vaudrait mieux considérer que cela correspond à ce qu’on appelle en grammaire classique une phrase), et un langage comme un ensemble de mots.

L’ensemble de tous les mots est noté \(A^*\). Bien qu’il paraisse bien éloigné des mathématiques, on peut le munir d’une opération d’apparence un peu absurde: si on a deux mots \(U\) et \(V\), leur produit \(UV\) est le mot obtenu en les concaténant, c’est-à-dire en les écrivant l’un à la suite de l’autre; cette simple opération permet de poser des questions non évidentes; par exemple, à quelle condition deux mots \(U\) et \(V\) commutent-ils, c’est-à-dire que \(UV=VU\)? On peut montrer que c’est le cas si et seulement s’ils sont tous les deux formés par la répétition d’un même mot.

Grammaires et machines

Les premières questions qui se posent sont de spécifier des langages, et de savoir reconnaître si un mot donné appartient à un certain langage; c’est l’une des premières fonctions des logiciels de programmation, et tous ceux qui ont appris à programmer connaissent la réponse « Syntax Error » de l’ordinateur qui dit que le programme est mal formé, souvent par l’oubli d’une parenthèse ou d’une virgule.

Il y a plusieurs manières de spécifier un langage: on peut décrire tous ses mots, ou bien en donner une grammaire, ou encore fabriquer une machine qui le reconnaît. Voici un exemple très simple: le langage d’or est formé de tous les mots sur l’alphabet \(\{0,1\}\) qui ne contiennent pas deux \(1\) consécutifs (il est ainsi nommé à cause des relations qu’il entretient avec le nombre d’or et la suite de Fibonacci). On peut le définir à partir de la grammaire suivante:

\[\begin{cases}
A::=e\mid A0\mid B0\\
B::=A1
\end{cases}\]
Ici, \(e\) représente le mot vide (qui n’a aucune lettre), \(A\) représente n’importe quel mot du langage d’or qui finit par \(0\) ou le mot vide, et \(B\) n’importe quel mot du langage d’or qui finit par un \(1\). Cette grammaire dit que, si un mot du langage d’or finit par un \(1\), le mot obtenu en effaçant ce \(1\) final est vide, ou est un mot du langage qui finit par un zéro.

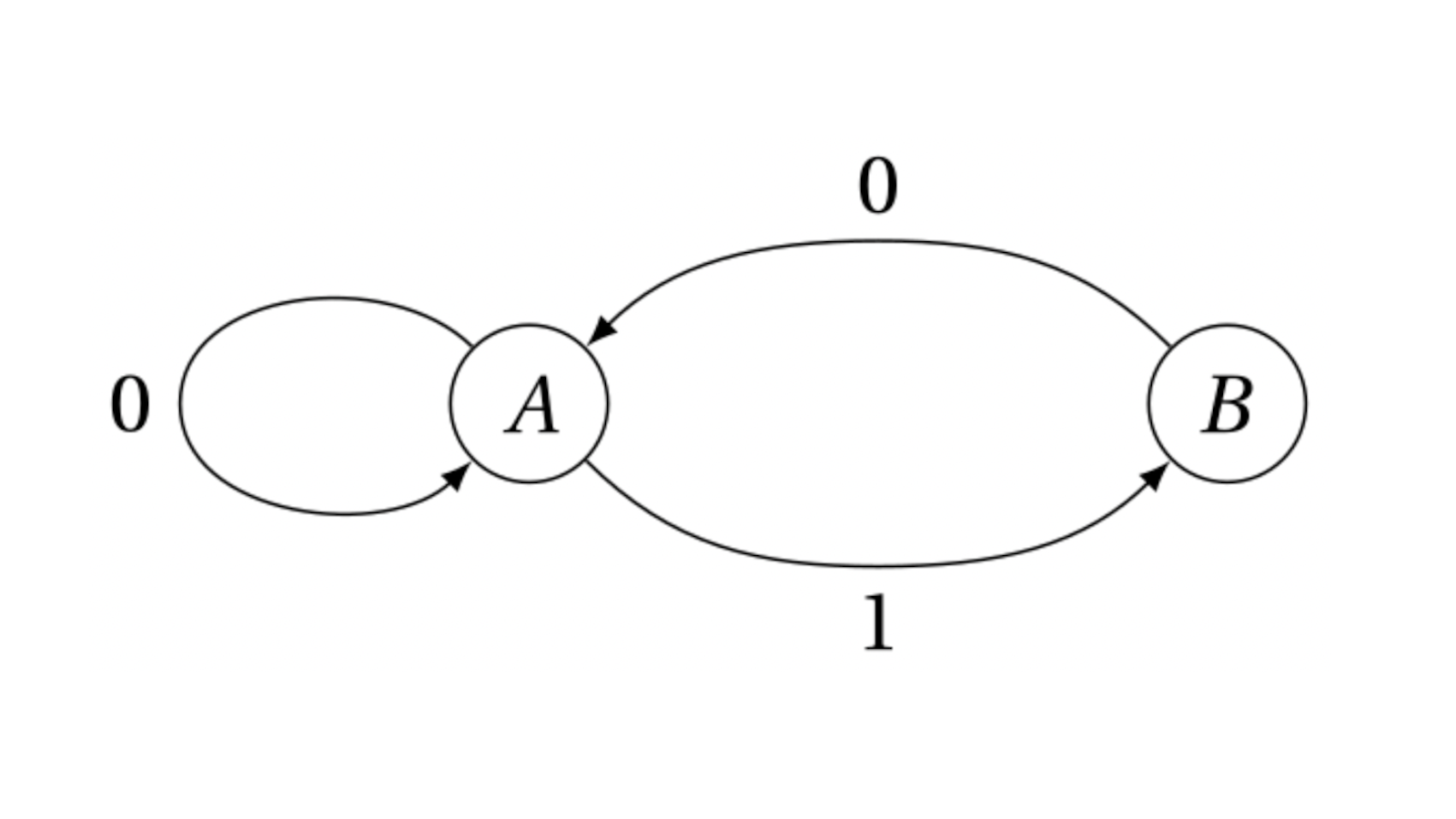
On peut aussi le reconnaître avec une machine très simple qui lit les lettres du mot une à une:

On part de l’état \(A\); si on lit une lettre \(0\), on y reste, et si on lit une lettre \(1\), on passe dans l’état \(B\). Si on lit une lettre \(1\) dans l’état \(B\), la machine bloque et le mot n’est pas reconnu, et si on lit un \(0\) on revient en \(A\). Si on peut arriver au bout du mot, il est dans le langage.

Classification des langages

On peut définir divers types de machines et de langages, et il existe toute une hiérarchie inventée depuis les années 50, qui est fondamentale pour la conception des langages informatiques, avec des langages de complexité variée. Par exemple, le langage d’or peut être reconnu de façon purement locale, en regardant les couples de lettres consécutives; ce n’est pas le cas d’un autre langage très naturel, le langage des parenthèses, qui décrit des parenthèses qui se ferment correctement, avec autant de parenthèses ouvrantes que de fermantes, et qui est donné par la grammaire très simple suivante:

\[S::=e\mid SS\mid (S)\]

Ce langage ne peut pas être reconnu de façon locale, car il faut s’assurer que toutes les parenthèses ouvrantes ont bien été refermées, donc il faut une mémoire arbitrairement grande.

Si cette classification fonctionne très bien pour des langages artificiels comme les langages de programmation, les langages «naturels» restent difficiles à décrire de cette façon, et rentrent mal dans les cases (entre autres parce qu’il est difficile de séparer la syntaxe, c’est-à-dire les règles de grammaire qui décrivent l’agencement des mots, et la sémantique, c’est-à-dire le rapport au sens et au monde que le langage décrit).

Algorithmique du texte

Une autre application de la théorie des langages est l’étude des algorithmes sur les mots, permettant par exemple de retrouver toutes les occurrences d’un mot dans un texte. De tels algorithmes sont aujourd’hui très utilisés, et ont trouvé un nouveau domaine d’application dans l’étude du génome, que l’on peut considérer comme un mot de très grande taille sur un alphabet à quatre lettres…