
Il est plaisant de célébrer Lagrange (25 janvier 1736 – 10 avril 1813), à coup sûr l’un des plus admirables mathématicien de la fin du XVIIIe siècle, illustre entre autres pour ses résultats en calcul des variations (dès les années 1750) et en mécanique céleste (son livre de Méchanique analitique fut publié en 1788).
Plusieurs articles sur ce site, ici et là, ainsi qu’un film récent, m’invitent à revenir à Lagrange, et plus précisément à deux de ses théorèmes qu’on peut énoncer de manière concise : l’un concerne les sommes de quatre carrés et l’autre les ordres des sous-groupes d’un groupe fini. Je me propose en particulier de raconter avec ces deux exemples comment le statut ou l’énoncé d’un théorème peut varier avec le temps.
-

Joseph-Louis Lagrange
Le théorème des quatre carrés
Certaines des contributions les plus profondes de Lagrange s’énoncent avec un minimum de vocabulaire technique. Ainsi :
tout nombre entier est aussi égal à la somme de quatre ou d’un moindre nombre de carrés entiers.
La phrase est copiée de son article de 1770 1
Joseph Louis de Lagrange, démonstration d’un théorème d’arithmétique, Nouveaux Mémoires de l’Académie royale des Sciences et Belles-Lettres de Berlin, année 1770. Oeuvres de Lagrange 3, pages 189–201. .
Par exemple : \(2 = 1^2 + 1^2\) et \(2014 = 44^2 + 7^2 + 5^2 + 2^2\).
Aujourd’hui, on dit souvent que «tout nombre entier positif est une somme de quatre carrés», en acceptant les zéros : \(2 = 1^2 + 1^2 + 0^2 + 0^2\).
Le résultat était connu auparavant, de Fermat (peu après 1600 – 1665), Bachet de Méziriac (1581 – 1638), et peut-être même Diophante (IIIe siècle). Euler (1707 – 1783) avait des parties de la démonstration, et Fermat a affirmé en avoir une démonstration complète, mais sans la publier 2Voir L.E. Dickson, History of the theory of Numbers, Volume II, page 275.. Le mérite de Lagrange est d’avoir fourni la première démonstration complète et publique.
Le statut du théorème a donc varié au cours du temps, passant d’une affirmation non démontrée au véritable « théorème de Lagrange », que Lagrange lui-même appelle « Théorème de M. Bachet ». Pour raconter la suite de l’histoire, il faudrait mentionner entre autres quelques-unes au moins des nombreuses démonstrations ultérieures, les raffinements, et les nouvelles questions motivées par le théorème. Les amateurs de hors-piste sont invités à en lire davantage 3Un article d’André Weil « Sur les sommes de trois et quatre carrés », in L’Enseignement Mathématique 20 (1974), 215—222 et la thèse de Jenny Boucard (2011) « Un rapprochement curieux de l’algèbre et de la théorie des nombres : études sur l’utilisatin des congruences en France de 1801 à 1850 », en particulier son chapitre 5
« Les travaux d’Euler et de Lagrange autour du théorème des quatre carrés – vers une théorie des résidus »..
Pour terminer, notons d’abord que certains nombres \(n\), par exemple 4 ou 7 peuvent s’écrire comme sommes de quatre carrés non nuls. D’autres nécessitent au moins un zéro ; leur liste commence par 0, 1, 2, 3, 5, 6, 8, 9, 11,14, 17, 24, 29, 32, 41, 56, 96, … 4Voir la “On-Line Encyclopedia of Integer Sequences® (OEIS®)” et plus précisément ceci .
Notons enfin que certains nombres \(n\), par exemple \(n=2\), n’ont qu’une seule écriture de la forme \(n = a^2 + b^2 + c^2 + d^2\) avec \(a \ge b \ge c \ge d \ge 0\) ; d’autres en ont plusieurs, comme \(4 = 2^2 + 0^2 + 0^2 + 0^2 = 1^2 + 1^2 + 1^2 + 1^2\).
La liste des nombres qui n’ont qu’une telle écriture commence par \(0, 1, 2, 3, 5, 6, 7, 8, 11, 14, 15, 23, 24, 32, 56, 96, …\)5Voir On-Line Encyclopedia of Integer Sequences® (OEIS®).

Tableau rouge (de Staël)
Le théorème sur les sous-groupes, aujourd’hui
L’autre résultat de Lagrange que nous voulons évoquer ici ne prend tout son sens que dans le cadre d’une théorie mathématique plus élaborée, la théorie des groupes ; c’est l’objet de plusieurs contributions sur ce site 6 Voir parmi d’autres Soit G un groupe et Un concept mathématique, trois notions : Les groupes au XIXe siècle chez Galois, Cayley, Dedekind ainsi que Un peu de géométrie des groupes. Pour la suite, il est pratique d’avoir à disposition quelques termes du vocabulaire de cette théorie, et il convient donc de colorier depuis ici ce billet en un bon rouge soutenu.
Commençons par énoncer le « théorème de Lagrange » dans sa forme moderne, comme on le trouve à la page 25 du Traité des substitutions et des équations algébriques de Camille Jordan, publié en 1870 (qu’il est possible de voir intégralement ici).
Théorème
Si le groupe \(H\) est contenu dans le groupe \(G\),
son ordre \(n\) est un diviseur de \(N\), ordre de \(G\).
Autrement dit : le nombre \(N\) des éléments de \(G\) est un multiple du nombre \(n\) des éléments de \(H\). Il est sous-entendu que le groupe \(G\) est fini.

Camille Jordan
Ainsi, si \(G\) est le groupe des rotations de l’espace qui transforment un triangle avec trois côtés égaux en lui-même, qui est un groupe «d’ordre six», c’est-à-dire un groupe à six éléments, \(G\) possède des sous-groupes ayant un, deux, trois, ou six éléments, mais aucun sous-groupe à quatre ou à cinq éléments. (On accepte les deux sous-groupes dits triviaux, qui sont le groupe réduit à l’identité, d’ordre un, et le groupe tout entier, ici d’ordre six.)
Autre exemple : si \(G\) est le groupe des rotations de l’espace qui transforment un tétraèdre avec six côtés égaux en lui-même, qui est un groupe d’ordre douze, le théorème de Lagrange établit que l’ordre d’un sous-groupe de \(G\) peut être a priori un, deux, trois, quatre, six, ou douze ; il se trouve que cinq de ces six nombres sont effectivement réalisés
par des sous-groupes de \(G\), mais qu’il n’existe aucun sous-groupe à six éléments.
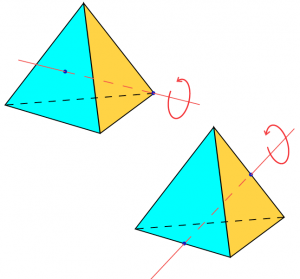
Rotations d’un tétraèdre régulier
Un énoncé impossible au temps de Lagrange
Qu’est-ce qu’un groupe ? Il y a plusieurs réponses possibles. Nous empruntons l’essentiel de la suite à l’article « The history of symmetry and the asymmetry of history » de Peter Neumann, publié en 2008.
L’une des définitions consiste à décréter que c’est un groupe de permutations d’un ensemble fini. En d’autres termes, si on considère un nombre \(N\) et la suite des entiers \((1, 2, …, N-1, N)\), une famille convenable de réarrangements de la suite constitue les éléments d’un groupe.
Ainsi, pour \(N=4\), les trois réarrangements \((1,2,3,4)\), \((2,3,1,4)\), \((3,1,2,4)\) sont les éléments d’un groupe de permutations d’ordre \(3\). Cette définition suffit à une grande partie de la théorie des groupes du XIXe siècle,
celle des «groupes de permutations».
Les géomètres aiment bien définir un groupe comme un groupe de symétries d’un objet (si possible géométrique). Les exemples évoqués plus haut, associés à un triangle équilatéral et à un tétraèdre régulier, se conforment à cette définition.
Pour jouer à établir une longue liste de définitions, les mathématiciens pourront s’inspirer du blog de Terence Tao.

.
L’énoncé de Lagrange
Le problème avec ces définitions est qu’aucune d’entre elles n’existait à l’époque de Lagrange. La notion de groupe n’émerge en effet qu’au cours du XIXe siècle (Cauchy, Gauss, Galois, …). Le théorème tel que formulé ci-dessus n’est donc en aucun cas dû à Lagrange.
La recherche des solutions des équations de la forme
$$
a_0 x^N + a_1 x^{N-1} + … + a_{N-1}x + a_N = 0,
$$
a été une activité centrale en mathématiques pendant une très longue période, en particulier entre la fin du XVIe siècle et le début du XIXe, pour Viète, Fermat, Descartes, d’Alembert, Lagrange, Gauss, Galois, Abel, et bien d’autres. Voir 7Jean-Pierre Tignol, « Galois’ theory of algebraic equations », World Scientific, 2001 ; en particulier le chapitre 10..
Dans son mémoire de 1770/71 consacré à ce sujet, Lagrange est amené à considérer une équation du type
$$
f(x_1, x_2, …, x_N) = 0,
$$
où \(f\) est un polynôme en les variables \(x_1, x_2, …, x_N\), variables qui correspondent aux \(N\) solutions
d’une équation de la forme précédente.
Au § 97 de son mémoire, Lagrange s’intéresse au nombre \(k\) de valeurs différentes que peut prendre \(f\) si on permute les variables. Par exemple, pour \(N=3\), ce nombre peut valoir \(1, 2, 3\) ou \(6\), comme le lecteur pourra le vérifier,


peut-être avec quelques indications :
Pour \(N=3\), il est pratique d’écrire \(x,y,z\) au lieu de \(x_1, x_2, x_3\).
Si \(f(x,y,z) = x+y+z\), nous avons \(x+y+z = y+x+z = x+z+y = … \) (six cas),
et par conséquent \(k=1\).
Si \(f(x,y,z) = x^2 y + y^2 z + z^2 x\), nous avons par exemple
\(f(1,2,3) = 2 + 12 + 9 = 23\) \(f(2,1,3) = 4 + 3 + 18 = 25\), et \(k=2\).
Si \(f(x,y,z) = x+yz\), nous avons par exemple
\(f(2,3,4) = 14\), \(f(3,4,2) = 11\), \(f(4,2,3) = 10\), et \(k=3\).
Si \(f(x,y,z) = x + y^2 + z^3\), nous avons \(k=6\),
comme on le vérifie en choisissant pour \(x,y,z\)
les valeurs \(1,2,3\), dans leurs six ordres possibles.
On se convainc facilement que le nombre \(k\) est toujours au plus \(6\) (ou au plus \(N!\)
8 On écrit \(N!\) pour «\(N\) factorielle», c’est-à-dire pour le produit de tous les entiers entre \(1\) et \(N\).
Par exemple~: \(4! = 1 \times 2 \times 3 \times 4 = 24\). pour \(N\) variables). Mais l’intuition de Lagrange lui a fait voir que, en plus d’être majoré par \(N!\),
le nombre \(k\) est un diviseur de \(N!\)
Pour \(N=3\), il n’existe donc aucun polynôme \(f(x,y,z)\) pouvant prendre exactement quatre valeurs ou exactement cinq valeurs.
Aujourd’hui, on comprend bien que le nombre \(k\) est le quotient de l’ordre du groupe des permutations de \(N\) lettres par l’ordre du groupe des symétries de l’équation \(f=0\), en particulier que \(N!\) est un multiple de \(k\)
(voir ci-dessus l’énoncé de Jordan du «théorème de Lagange»). Mais Lagrange lui-même n’a jamais écrit son résultat dans le cadre de la théorie des groupes, pour la simple raison que celle-ci n’existait pas encore de son temps.
Ceci dit, une lecture attentive du § 97 révèle que l’argument par lequel Lagrange justifie son énoncé n’est pas correct. Les experts du sujet savent qu’on trouve des preuves satisfaisantes chez Abbati en 1802, et de nouveau chez Cauchy en 1815. La forme du théorème que nous connaissons aujourd’hui se trouve dans la lettre de Galois à Chevalier du 29 mai 1832, mais ne fut largement connue et acceptée qu’après la 3e édition du \emph{Cours d’algèbre supérieure} de Serret (1866) et le Traité des substitutions et des équations algébriques de Camille Jordan, déjà cité.
Le «théorème de Lagrange» a donc lui aussi varié : d’abord une intuition brillante pour les nombres possibles des valeurs de \(f(x_1, x_2, …, x_N)\), ensuite ce même premier énoncé rigoureusement démontré, et presqu’un siècle après Lagrange un autre énoncé, celui qui est le plus connu aujourd’hui.
Fluctuat nec mergitur, c’est pas d’la littérature 9A écouter intégralement ici.

Georges Brassens
Post-scriptum
Je remercie Frédéric Brechenmacher pour ses indications.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.