
Je viens de terminer la lecture de ce bouquin de Reviel NETZ et William NOEL, dont la traduction française vient de paraître chez JC Lattès.
Je l’ai lu comme un roman policier : d’une traite. La destinée de l’œuvre d’Archimède est passionnante et un billet ne suffirait pas à la raconter (d’autant plus que je n’en connais que ce qu’on en dit dans ce livre). Des manuscrits recopiés, d’abord sur des rouleaux, puis sur du parchemin. Des textes éternels écrits il y a plus de 2 200 ans :
De l’équilibre des figures planes, La Quadrature de la parabole, De la sphère et du cylindre, Des spirales, Sur les conoïdes et les sphéroïdes, Des corps flottants, De la mesure du cercle, L’arénaire, La catoptrique, De la méthode.
On en suit la trace au cours des siècles, des invasions par des « barbares » ou par des croisés chrétiens… Des livres disparaissent, d’autres réapparaissent. En 1906, à Constantinople, on trouve un palimpseste contenant un livre inédit d’Archimède (la Méthode). Un palimpseste est un parchemin qui a été réutilisé : le scribe a gratté le texte original (d’Archimède dans ce cas) et a copié par dessus un texte beaucoup moins intéressant (dans ce cas). Et puis, ce palimpseste disparaît à nouveau pour refaire surface dans une salle des ventes à New York en 1998 où il est vendu pour deux millions de dollars.
Dans ce livre, on parle d’histoire, de maths, d’histoire des maths, mais aussi des techniques modernes employées pour préserver les manuscrits rares ou pour parvenir à lire un texte qui a été gratté et par dessus lequel est écrit un autre texte qui ne vous intéresse pas. Mais le livre de Netz et Noel est facile à lire – pas besoin de lumière ultraviolette – même si on ne connaît pas grand chose à l’histoire de la géométrie grecque. Passionnant.
Je voudrais signaler deux aspects qui m’ont particulièrement intéressé.
Le premier concerne le rôle des figures dans la mathématique grecque, et en particulier dans la géométrie d’Archimède. Bien sûr, on n’a pas d’originaux des figures qui illustraient les textes d’Archimède : ils ont été copiés, copiés, et copiés encore. Les copistes ont-ils tendance à améliorer les figures, ou au contraire à les déformer s’ils ne les comprennent pas ? Aujourd’hui, les experts examinent les figures sur les diverses copies, trouvent des points communs, des différences, et essayent d’en tirer des conclusions sur les figures originelles. Je suis l’heureux propriétaire de deux beaux volumes sur Archimède 1Arquímedes, Obras escogidas, deux volumes édités par Durán, Real Sociedad Española, Madrid 2006. Le premier contient un facsimilé d’une copie du livre La sphère et le cylindre datant du seizième siècle. Le deuxième contient en particulier une traduction moderne du premier et il est intéressant de constater que le traducteur a également « traduit » les figures ! Voici par exemple une figure que j’ai scannée à partir du facsimilé :
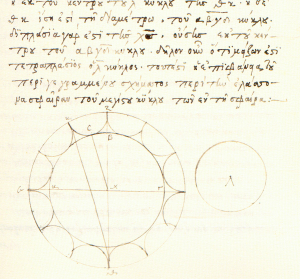
.
et sa « traduction » moderne
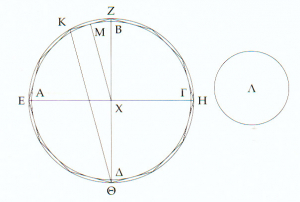
.
Que constate-t-on ? Le polygone dont les côtés sont curvilignes dans le manuscrit est devenu un « vrai » polygone avec des côtés rectilignes dans la traduction. Peut-on penser qu’Archimède ne savait pas dessiner un segment rectiligne ? Pourtant, quand on lit le texte, on comprend bien qu’il s’agit effectivement de segments rectilignes… Voici l’interprétation qu’on trouve dans le livre de Netz et Noel (encore une fois, n’étant pas spécialiste de ces choses, je ne sais pas si cette interprétation est « bien connue », ou si au contraire elle est « bien connue comme étant fausse »… ). La géométrie grecque est centrée sur la figure, et le texte ne fait qu’accompagner la figure. Mais bien sûr, lorsqu’on démontre un théorème valable par exemple pour tous les triangles, et lorsqu’on fait une figure, on dessine un triangle particulier, alors qu’on aimerait dessiner tous les triangles. Ceci peut être trompeur. Il peut donc être judicieux de faire des figures qui sont délibérément fausses, qui ne visent pas à dessiner un triangle mais plutôt l’idée de triangle. On peut donc dessiner les côtés du triangle comme étant courbes. Le polygone d’Archimède n’est donc pas un polygone particulier, c’est un dessin qui évoque tous les polygones. Certains reconnaîtront le vieil adage « la géométrie est l’art de raisonner juste sur des figures fausses »… Aujourd’hui, à l’heure des logiciels de dessin, des méthodes de visualisation 3D etc., cet enseignement d’Archimède mérite peut-être réflexion. Pour enseigner la géométrie, pour « faire » de la géométrie, les méthodes « rustiques » sont peut-être les meilleures. Les jolies figures parfaites sur ordinateurs sont trop particulières ? N’oublions pas le tableau noir et les dessins à la craie, à main levée.
Une autre idée contenue dans ce livre : Archimède serait à l’origine de la « combinatoire » ? Je dois dire que la démonstration du chapitre 10 sur le Stomachion ne m’a pas semblé totalement convaincante mais elle est séduisante. Il s’agit d’un livre d’Archimède dont on ne connaît presque rien en fait : quelques pages énigmatiques et une copie tardive arabe, probablement très différente de l’original. Un jeu de puzzle. Un carré est décomposé en 14 morceaux de la manière suivante :
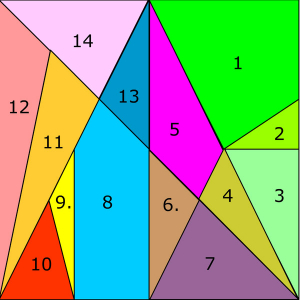
.
Cela fait penser au TamGram auquel j’ai pas mal joué il y a longtemps. Pourquoi ce puzzle intéressait-il Archimède ? Netz et Noel pensent qu’il s’agit du premier problème combinatoire de l’histoire. Avec ces quatorze pièces, de combien de manières peut-on reconstituer un carré ? Le livre raconte comment des mathématiciens et des informaticiens ont résolu le problème très récemment : la réponse est 17 152. Cette « découverte » a même eu les honneurs d’un article du New York Times en 2003 : « In Archimedes’ Puzzle, a New Eureka Moment » ! Archimède avait-il trouvé ces 17 152 solutions ? Comment le savoir puisque le livre est perdu. Mais peut-être la réponse arrivera-t-elle cachée dans un palimpseste qu’on retrouvera dans un siècle ?
Des livres écrits il y a 2200 ans dont on parle encore aujourd’hui…


18h00
L’article donne très envie de lire ce livre. Je suis cependant très sceptique quant à l’interprétation des lignes curvilignes à la place de segments rectilignes, dans la figure du manuscrit du 16ème siècle, pour la raison suivante. Les Grecs savaient parfaitement faire la différence entre une figure dessinée (représentant par exemple un triangle particulier) et la figure idéale désignant tous les triangles, ou un triangle quelconque. Ils faisaient même mieux la différence que nous, puisqu’ils utilisaient deux termes distincts : διάγραμμα (diagramme)pour le premier et σχήμα (schéma)pour le second. Voici un texte de Platon précisant bien cette différence :
“en outre [ceux qui s’occupent de géométrie] font usage de figures visibles (διάγραμμα), et sur ces figures ils construisent des raisonnements sans avoir à l’esprit ces figures elle-mêmes, mais les figures parfaites (σχήμα) dont celles-ci sont des images(…) Toutes ces figures qu’ils modèlent ou dessinent, qui portent des ombres et produisent des images dans l’eau, ils les emploient comme si c’étaient aussi des images, pour arriver à voir ces objets supérieurs qu’on n’aperçoit que par la pensée. »
( Platon : La République :chap. VI, 510 c–e)
Dans le célèbre épisode de la « Vie des hommes illustres » retraçant la mort d’Archimède, Plutarque écrit :
il était seul avec lui – même, en train d’examiner quelque chose sur une figure tracée (διαγράμματος), et, ayant donné à la contemplation à la fois sa pensée et son regard, il ne perçut rien ni des Romains qui couraient partout, ni de la ville prise » (Plutarque, Vie des hommes illustres, chap. VII)
Et lorsque Euclide parle des figures (déf. 14 du Livre I par exemple), il utilise toujours le mot σχήμα
19h49
Merci pour votre commentaire. Vous êtes visiblement bien plus savant que moi sur ces questions et je me garderais bien de commencer un débat sur ce sujet ! Les auteurs du livre me semblent des spécialistes reconnus mais ça ne veut pas dire qu’ils ont raison, bien sûr. La discussion est donc ouverte… Quoi qu’il en soit, l’idée de raisonner sur des figures imprécises me semble séduisante 🙂
10h00
je n’ai pas appris le grec mais j’ai eu l’occasion à plusieurs reprises de constater la subtilité de cette langue et sa richesse de vocabulaire. En revenant à la version grecque du texte cité de Platon, je m’aperçois que j’ai extrapolé et que ça ne colle pas avec le vocabulaire utilisé par Platon. Cela ne remet pas en cause, je pense, le fait que Platon distingue vraiment dans ce texte la figure dessinée et la figure pensée, mais simplement que le vocabulaire grec est beaucoup plus subtil et varié que notre langage du « blanc ou noir », ou du « oui ou non ». Platon utilise ici le mot « graphos » = « écritures » ou « pièces écrites ». Sur la distinction « diagramma », « sgema » on peut aussi se reporter à la page 161 du volume I de la récente traduction française des éléments d’Euclide par Vitrac.