
Ce qu’il y a de bien avec la racine carrée de 2, c’est qu’on la rencontre partout, un peu comme une amie qui ne s’éloignerait jamais.
Pour les besoins d’un article « sérieux » de mathématiques, je me suis repenché sur une méthode d’approximation de \(\sqrt{2}\) connue dès l’époque babylonienne et qui consiste, en partant d’un rectangle de côtés 1 et 2, à construire une suite de rectangles d’aire 2 et dont la longueur est la moyenne (arithmétique) des dimensions du rectangle précédent. Les premiers rectangles sont les suivants :

Comme on le visualise, cette méthode est si efficace qu’au bout du troisième rectangle on ne discerne déjà plus la différence avec un vrai carré. Or puisque les aires des rectangles sont supposées toutes égales à 2, le carré limite est de côté \(\sqrt{2}\). En conséquence, largeurs et longueurs des rectangles successifs sont des approximations de \(\sqrt{2}\) (par excès et par défaut), de plus en plus précises.
Cette méthode est effectivement très rapide. On la dit quadratique, mot savant qui indique pour l’essentiel que le nombre de décimales exactes double à chaque nouveau rectangle.
Dans ce qui précède, \(\sqrt{2}\) est vu comme le nombre qui, multiplié par lui-même, donne 2 (autrement dit, comme le côté d’un carré d’aire 2). Parmi les autres caractérisations possibles de \(\sqrt{2}\), il y a celle qui est à l’origine de nos formats de papier : \(\sqrt{2}\) est le rapport longueur/largeur à choisir pour un rectangle \(R\) qui, une fois plié parallèlement à sa largeur, produit un rectangle \(R’\) pour lequel le rapport des dimensions est lui aussi de \(\sqrt{2}\).
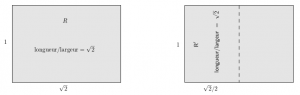
Peut-on utiliser cette définition alternative pour produire des approximations de \(\sqrt{2}\) ? me suis-je demandé. La réponse est oui, et voici comment. Si les dimensions de \(R\) sont \(a\) et \(b\) (avec \(a\geq b\)), alors celles de \(R’\) sont \(a/2\) et \(b\). Nous cherchons donc \(a\) et \(b\) tels que \(a/b = b/(a/2)\) (notez que \(R’\) est « dans l’autre sens »).
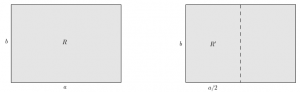
Une propriété assez simple à visualiser est que si \(R\) est trop long, c’est-à-dire que \(a/b\) est plus grand que \(\sqrt{2}\), alors \(R’\) ne l’est pas assez, c’est-à-dire que \(b/(a/2)\) est, lui, inférieur à \(\sqrt{2}\) (et inversement). À moins d’être d’emblée égaux à \(\sqrt{2}\), les rapports \(a/b\) et \(b/(a/2)\) sont donc situés de part et d’autre de \(\sqrt{2}\). Une façon simple de s’approcher de \(\sqrt{2}\) consiste alors à prendre un rectangle dont le rapport longueur/largeur est la moyenne (arithmétique) de \(a/b\) et \(b/(a/2)\). Le nouveau rectangle \(R\) construit sur ce rapport produit par pliage un nouveau rectangle \(R’\), la moyenne des rapports longueur/largeur de \(R\) et \(R’\) conduisent à définir un nouveau rectangle, et ainsi de suite. En posant, pour fixer les idées (puisque seul compte le rapport des dimensions) que \(R\) est toujours de largeur 1, voici ce que cette idée donne à partir d’un rectangle \(R\) initial tel que \(a = 2\) et \(b = 1\) (pour simplifier, la largeur de chaque nouveau rectangle \(R\) est toujours prise égale à 1).

Ça vous dit quelque chose ? C’est bien ça : les nombres obtenus sont les mêmes que ceux de l’algorithme des Babyloniens. Et plutôt que de considérer cette méthode comme une présentation alternative d’un algorithme d’approximation de \(\sqrt{2}\), on peut aussi l’écrire comme une démonstration de ce que les rectangles \(R\) pour lesquels \(R’\) a la même forme que \(R\) sont ceux qui satisfont à l’égalité longueur/largeur = \(\sqrt{2}\).
Ce n’est pas avec un résultat pareil qu’on m’offrira un pont d’or à Princeton ou à Harvard, mais c’est ce genre de petites perles qui aident à aimer son métier de chercheur. Et s’il n’est pas sûr que j’arrive à caser cette observation dans mon article « sérieux », je vais quand même essayer. En le glissant à la fin, là où plus personne ne lit…




14h57
Voir les 6 commentaires