
Il y a un peu plus d’un an paraissait un essai plaisant de Pierre Bayard intitulé Comment parler des livres que l’on n’a pas lus ? Dans le prologue on peut lire :
Enseignant la littérature à l’université, je ne peux […] échapper à l’obligation de commenter des livres que, la plupart du temps, je n’ai pas ouverts (p. 13).
Outre qu’en remplaçant « la littérature » par « les mathématiques » je pourrais faire mienne cette phrase, je mentionne cet essai car, dans une approche scientifique et naturaliste, Pierre Bayard y propose de classifier les livres en quatre catégories :
- LI : livre inconnu
- LP : livre parcouru
- LE : livre évoqué
- LO : livre oublié
et distingue quatre avis possible :
- ++ : avis très positif
- + : avis positif
- – : avis négatif
- – – : avis très négatif.
J’attribuerais au livre de Bayard un (LP,+). Mais ce n’est pas le sujet. L’auteur dont je veux parler est Thomas Pynchon. Le problème est que, bien que je classe tous ses livres dans la catégorie (LE, ++), seuls deux d’entre eux ( V. disponible dans la collection point seuil, et le tout récent Contre-jour paru en français au Seuil à la rentrée) entrent (de justesse) dans la catégorie (LP). Mais, me direz-vous, pourquoi chercher à parler de livres que l’on n’a pas lus ? Ma première réponse sera de vous renvoyer au livre de Bayard, que je ne saurais (faute de place, mais aussi parce que je ne l’ai pas lu jusqu’au bout !) résumer ici. Ma deuxième réponse vient de ce qu’une partie de la fascination qu’exerce (sur moi ?) Pynchon est très certainement liée aux mathématiques, et donc pas sans lien avec ce site.
Car en effet Pynchon est indéniablement un auteur qui possède une culture scientifique et surtout mathématique au-dessus de la norme (pour un écrivain). C’est encore plus frappant dans Contre-jour où Pynchon convoque en particulier toute une assemblée de mathématiciens qui
[…] tout en buvant un café semi-liquide et en grignotant des beignets […] revinrent sur la question des fonctions périodiques, et sur leur forme généralisée, les fonctions automorphiques (p. 515).
La traduction française, due à Claro et par ailleurs remarquable, est ici malheureuse, il n’existe point de « fonctions automorphiques ». Les fonctions dont parle ici Pynchon sont les fonctions automorphes dont la découverte par Poincaré et Klein est l’un des quelques faits majeurs des mathématiques du dix-neuvième siècle.
Mais alors, que sont donc ces fonctions automorphes dont nous parle Pynchon ?
Pour les décrire pensons ensemble à une partie de l’activité des mathématiciens : celle qui consiste à enrichir une « boîte à outils » dont les outils seraient des fonctions. Une première motivation pour se constituer une telle boîte à outils est très certainement d’aider les physiciens à coder leurs observations. Ainsi le mouvement d’un corps dans l’espace est-il codé par trois fonctions du temps : les trois fonctions coordonnées. Nous verrons que la motivation est également interne aux mathématiques.
Les premières fonctions de notre boîte à outils – appelées fonctions linéaires – rendent compte des mouvements linéaires uniformes. On l’aura compris, déjà trop limitées pour les applications physiques, elles sont loin d’exciter l’imagination de Pynchon dont le style n’est pas à proprement parler linéaire.
En fait, notre temporalité soi-disant linéaire se fonde sur un phénomène circulaire ou, si vous préférez, périodique – la rotation même de la Terre. Tout tourne, jusqu’à et y compris, probablement, l’univers tout entier (p. 514).
De nombreux phénomènes périodiques rythment en effet notre vie. Le soleil suit une trajectoire périodique et se lève (à peu près) toutes les 24 heures, la nouvelle lune revient tous les 29,5 jours, l’été revient à peu près tous les ans …
Ces cycles ont très tôt fasciné les mathématiciens qui ont cherché à les décomposer en phénomènes cycliques élémentaires.
Le plus élémentaire est le mouvement d’un point qui décrit un cercle autour d’un autre à vitesse angulaire constante. C’est le premier modèle auquel pensent les premiers observateurs du soleil (qui tourne « évidemment » autour de la terre).
Les mouvements du soleil et des autres planètes ne sont pas circulaires autour de la terre, il faut donc bien vite corriger ce modèle. Et guidé par une « mystique du cercle » les grecs de Hipparque à Ptolémé ont élaboré la théorie des épicycles : tout mouvement périodique peut-être approché par un nombre fini de mouvement circulaire uniforme. Enfant (ou plus tard) vous avez peut-être expérimenté cette théorie en jouant au spirographe. En voici un exemple :

.
Plutôt que d’ajouter toutes les fonctions périodiques dans notre boîte à outils, la théorie des épicycles nous apprend à n’ajouter que les fonctions plus élémentaires qui rendent compte du mouvement circulaire uniforme : les fonctions circulaires sinus et cosinus étudiées au lycée.
Ces fonctions permettent de paramétrer le cercle par un réel :
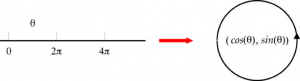
(Image empruntée à l’article d’Etienne Ghys : Géométriser l’espace : de Gauss à Perelman.)
Ce que l’on visualise mieux dans l’animation qui suit.

Insistons sur le fait que de cette image jaillissent toutes les merveilleuses propriétés des fonctions circulaires.
Au début du dix-neuvième siècle notre boîte à outils s’enrichit de nouvelles merveilles : les fonctions elliptiques. Ainsi nommées parce qu’elles permettent (entre autres) de calculer la longueur d’arc d’une ellipse, ces fonctions sont essentielles aussi bien en physique qu’en théorie des nombres. Ce sont des fonctions doublement périodiques. Il leur correspond l’image et l’animation suivante (téléchargeable ici ou visible en direct sur YouTube).
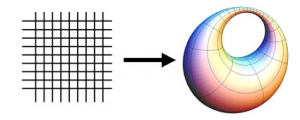
(Image empruntée à l’article d’Etienne Ghys : Géométriser l’espace : de Gauss à Perelman.)

Animation flash téléchargeable (1.5Mo)
Vidéo créée à l’Université de Hanovre – Groupe de Topologie – 2004
Voici donc des fonctions doublement périodiques. Est-ce assez pour notre écrivain ? Non, cette double périodicité est bien trop simplement agencée, sa symétrie se réalise dans le plan euclidien auquel nous sommes habitués. Il en faut plus à Pynchon :
Les Vectoristes et les Quaternionistes présents rappelèrent à tous la fonction qu’ils avaient récemment mise au point, connue sous le nom de fonction lobatchevskienne […] au moyen de laquelle, de façon presque annexe, l’espace euclidien ordinaire est transformé en espace lobatchevskien. (p. 515)
Et voilà ! Ce n’est pas dans l’espace euclidien qui nous est familier, que Pynchon veut nous projeter, mais dans l’ espace de Lobatchevki – ou espace hyperbolique – modèle d’une géométrie non-euclidienne (bien plus riche que notre géométrie euclidienne) dont la considération a permis à Poincaré et Klein d’enrichir notre boîte à outils de nouvelles fonctions : les fonctions automorphes. Comme les fonctions circulaires et elliptiques, on peut schématiser les fonctions automorphes par la figure suivante.
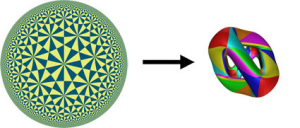
(Image empruntée à l’article d’Etienne Ghys : Géométriser l’espace : de Gauss à Perelman.)
L’animation correspondante est encore plus parlante en dimension 3 comme dans le superbe film Not Knot produite par feu le Geometry Center et disponible sur YouTube à l’adresse suivante (voir particulièrement la deuxième partie). Retenons de ce film l’image suivante qui représente l’espace de Lobatchevski.

.
Dans cette image tous les pavés (des dodécaèdres réguliers) doivent être pensés comme étant de la même taille (congruents). L’agencement, beaucoup plus compliqué que celui des parallèlogrammes d’un pavage du plan euclidien, n’est pas sans rappeler l’arborescence du site wiki lancé le jour de la parution américaine de Contre-jour afin d’aider les lecteurs à se repérer dans l’espace pynchonien, ses personnages, ses différents évènements et thèmes. 1À ceux qui trouverait d’ailleurs totalement disproportionnée mon insistance à vouloir lire des mathématiques dans le livre de Pynchon je conseillerais de consulter, à l’aide de ce site, les occurences de Gauss, Poincaré, Riemann, Klein, Fuchs, zeta function, automorphic … dans le livre.
Et les fonctions automorphes dans tout ça, à quoi peuvent-elles servir ? J’y reviendrai sûrement dans de prochains billets, qu’il me suffise de dire aujourd’hui qu’elles représentent un outil essentiel de la démonstration du célèbre théorème de Fermat par Andrew Wiles, ou encore de la toute récente preuve de la conjecture de Sato-Tate par Clozel, Harris, Taylor et Shepherd-Barron dont les articles, qui doivent être prochainement publiés aux publications mathématiques de l’I.H.E.S. , illustrent à merveille la catégorie (LE,++) en mathématiques.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.