
On a encore rogné les programmes de mathématiques dans le secondaire. Et comme d’habitude, c’est la géométrie qui en a eu le plus pour son compte (voir ici). Bientôt, il n’en restera pas grand chose et on s’en passera : on fera des maths où les nombres ne mesureront plus les longueurs, les aires, les volumes… mais que des quantités de dollars ! Ce billet est encore le cri du malheureux dans le fond du puits que personne n’entend jamais. Alors contentons-nous d’y montrer seulement quelques perles géométriques mises de côté et que les élèves des générations futures n’auront peut-être pas l’occasion de connaître. Quel dommage !
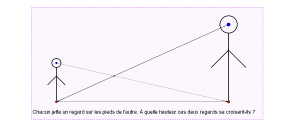
1. Angle inscrit et angle au centre
Une notion remarquable de la géométrie euclidienne plane et qu’on ne traitera plus au collège. Qu’est-ce qui motive sa suppression ?

Les deux angles \(\widehat{AMB}\) et \(\widehat{AOB}\) interceptent le même arc d’extrémités \(A\) et \(B\). Le premier est appelé {\it angle inscrit} et le second {\it angle au centre}. L’angle au centre est le double de l’angle inscrit {\it i.e.} \(\widehat{AOB}=2\widehat{AMB}\).
Le dessin de droite donne ce qu’il faut pour mener la preuve (qui est très élémentaire).

Conséquence : lorsque le point \(M\) varie sur l’arc \(AB\), sa mesure reste constante. En effet, cette mesure est la moitié de celle de l’angle au centre qui est le même quelle que soit la position de \(M\) sur l’arc en question.
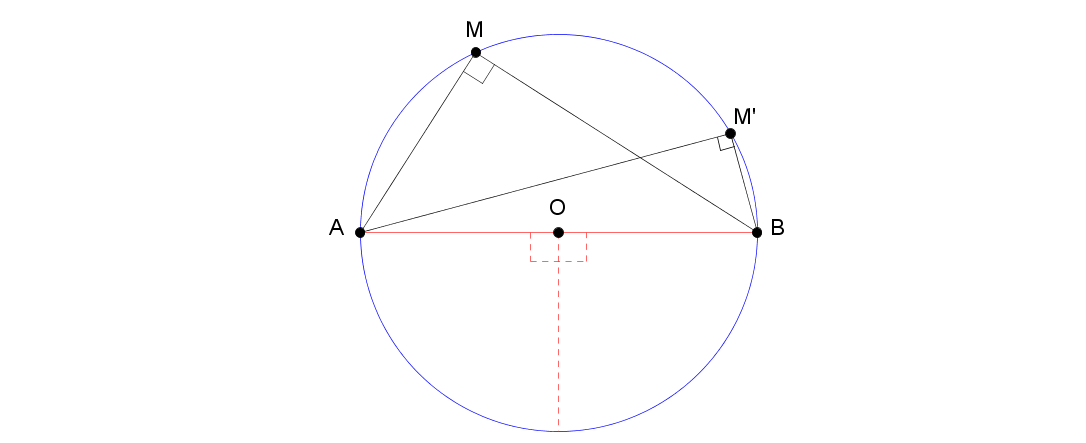
Le cas où la corde \(AB\) est un diamètre donne un angle droit \(\widehat{AMB}\). C’est la première propriété qu’évoquent les élèves de collège quand on leur parle d’angle inscrit et d’angle au centre. Mais elle vient d’être supprimée des programmes.

Un cas limite : l’angle formé par la corde \(AB\) et la tangente au point \(A\) est égal à tout angle inscrit \(\widehat{AMB}\) interceptant le même arc \(AB\). (Mais on ne parlera plus de tangente au collège.)
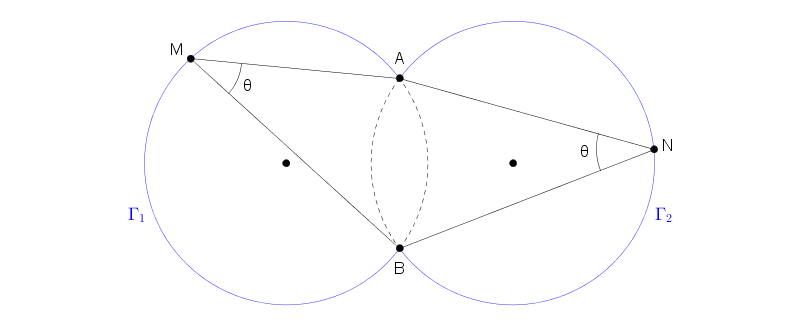
On se donne un angle de mesure \(\theta \) avec \(0<\theta <\pi \) et deux points \(A\) et \(B\) (distincts). Quel est le lieu géométrique \(\Gamma \) des points \(M\) vérifiant \(\widehat{AMB}=\theta \) ? (C’est l’endroit duquel on voit le segment \([AB]\) sous l’angle \(\theta \).


Réponse
Elle se voit déjà dans le dessin ci-dessus mais expliquons. On construit un point \(M\) tel que \(\widehat{AMB}=\theta \). Il n’est évidemment pas sur la droite \((AB)\) puisque \(0<\theta <\pi \). Ensuite, on trace le cercle qui passe par les points \(A\), \(B\) et \(M\). Celui-ci est partagé en deux arcs d’extrémités \(A\) et \(B\) ; on note \(\Gamma_1\) celui qui contient le point \(M\). Alors tout point de \(\Gamma_1\) est sur le lieu géométrique cherché. Le symétrique de \(\Gamma_1\) par rapport à la droite \((AB)\) est aussi un arc de cercle \(\Gamma_2\) qui possède la même propriété. L’ensemble \(\Gamma \) cherché est la réunion \(\Gamma_1\cup \Gamma_2\).
2. Du quelconque qui génère du régulier
Trois points pris au hasard n’ont aucune chance de former un triangle équilatéral. Et à défaut de le pouvoir, ils
sont toujours sur un même (et unique) cercle alors que presque sûrement quatre points ne peuvent pas l’être. Mais à tout triangle on sait associer un triangle équilatéral et à tout quadrilatère strictement convexe un quadrilatère inscriptible. Ce sont des objets produits à partir de droites remarquables (qui viennent aussi d’être bannies des programmes de collège).

Soient \(ABC\) un triangle, \((AM_1)\) et \((AM_3)\) les trisectrices de l’angle \(\widehat{BAC}\), \((BM_1)\) et \((BM_2)\) les trisectrices de l’angle \(\widehat{ABC}\) et \((CM_2)\) et \((CM_3)\) celles de l’angle \(\widehat{ACB}\).
Alors le triangle \(M_1M_2M_3\) est équilatéral. C’est le Théorème de Morley (un joyau de la géométrie plane).
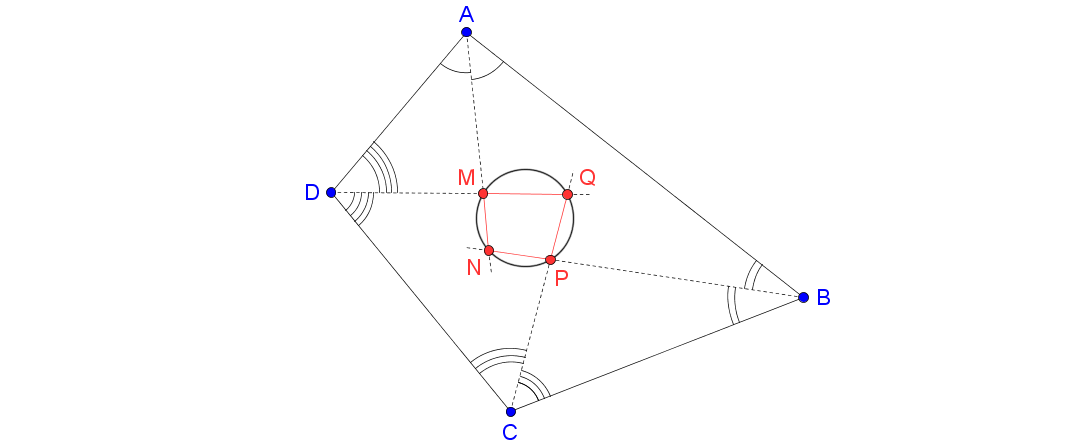
Soient \(ABCD\) un quadrilatère strictement convexe.
La bissectrice de \(\widehat{A}\) coupe celle de \(\widehat{D}\) en \(M\) et celle de \(\widehat{B}\) en \(N\). De même, la bissectrice de \(\widehat{C}\) coupe celle de \(\widehat{B}\) en \(P\) et celle de \(\widehat{D}\) en \(Q\). Alors le quadrilatère \(MNPQ\) est est inscrit dans un cercle.
3. Triangle inscrit à périmètre minimal
Comme les bissectrices, les hauteurs d’un triangle sont des droites remarquables et jouent aussi un rôle essentiel. Voici un bel exemple sur lequel on voit de quoi elles sont capables !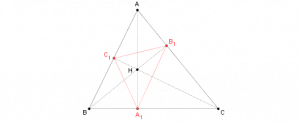
Soient \(ABC\) un triangle actuangle (tous ses angles sont aigus) et \(AA_1\), \(BB_1\), \(CC_1\) ses hauteurs.
Le triangle \(A_1B_1C_1\) est appelé {\it triangle orthique} de \(ABC\). Ses bissectrices sont les hauteurs \(AA_1\), \(BB_1\), \(CC_1\) et c’est le triangle inscrit dans \(ABC\) qui a le plus petit périmètre (Problème de Fagnano)
4. Un dernier : le problème \((a,b,c)\)
La résolution du problème qui suit mélange pas mal de propriétés et d’outils géométriques, par exemple les rotations qui, heureusement, sont de retour ! Le lecteur pourrait s’y adonner à partir du dessin offert ci-dessous.
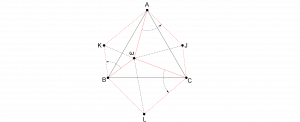
Soit \(ABC\) un triangle équilatéral. On s’y donne un point \(\omega \) intérieur et on pose \(a=\omega A\), \(b=\omega B\) et \(c=\omega C\). Calculer l’aire \({\cal A}(ABC)\) du triangle \(ABC\) en fonction de \(a\), \(b\) et \(c\).
J’ai croisé ce problème il y a quelques années en me baladant sur le net, posé dans le cas particulier \(a=3\), \(b=4\) et \(c=5\).


Réponse
\[{\cal A}(ABC)={1\over 2}\left\{ 3\sqrt{\lambda (\lambda -a)(\lambda -b)(\lambda -c)}+{\sqrt 3\over 4}(a^2+b^2+c^2)\right\} \]
où \(\lambda ={1\over 2}(a+b+c)\).
5. Épilogue
Ces objets géométriques qu’on délaisse petit à petit sont comme les fleurs, les plantes, les arbres… qu’on n’arrose plus et qui finissent par dépérir.
Que va-t-on enseigner en mathématiques dans un avenir proche ? À ce rythme, ce ne sera que des recettes dites « utiles », tout le reste on n’en aura rien à faire !





14h31
Voir les 18 commentaires