Un théorème et une « conjecture » de Marco

Nous avons appris avec consternation la disparition du mathématicien Marco Brunella.

Pour lui rendre hommage dans un site dédié aux mathématiques, je propose de décrire l’un de ses théorèmes et l’une de ses conjectures.

J’ai rencontré Marco à Rio en 1993, alors qu’il était en stage postdoctoral. J’ai été immédiatement impressionné par la clarté de sa vision mathématique. Nous avons tout de suite collaboré et je me souviens de la rédaction de l’article que nous avons écrit ensemble à l’époque. Lui italien, moi français, nous parlions portugais entre nous, et nous écrivions en anglais ! Marco cherchait à raccourcir le texte, à le restreindre au strict nécessaire. Quant à moi, je proposais des répétitions, pour que le lecteur puisse mieux comprendre. Mais Marco était intraitable ! Ses textes étaient à son image, d’une grande sobriété.

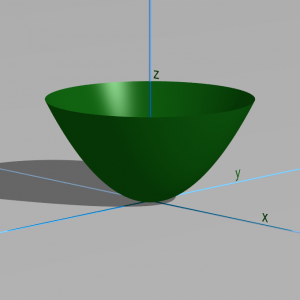
Voici l’un des problèmes les plus anciens qui se posent en mécanique. La figure suivante représente une cuvette.

.

Si on dépose une bille au fond de la cuvette, elle y reste… sans bouger. Si on donne un tout petit coup sur la bille, il est bien clair qu’elle va osciller autour de la position d’équilibre sans s’en écarter de beaucoup. On dit que la bille est dans un minimum de potentiel, dans une position d’équilibre stable. Le fait qu’un minimum soit toujours une position stable est un théorème de Lagrange, précisé plus tard par Dirichlet.

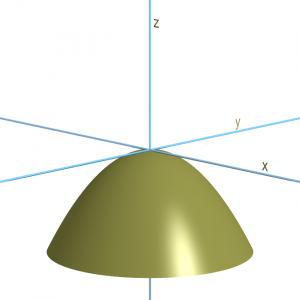
A l’inverse, si on dépose soigneusement une bille sur le sommet d’une montagne, elle sera en équilibre… instable. La moindre perturbation de la bille, le moindre souffle de vent, et la bille dévale la pente. Un maximum de potentiel est instable.

.

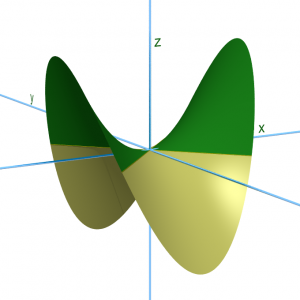
Dans la figure suivante, qui représente un col, il ne s’agit ni d’un maximum ni d’un minimum.

.

Là encore, il semble clair qu’il y a instabilité : si on pousse légèrement la bille, dans la bonne direction, elle tombe dans la vallée.

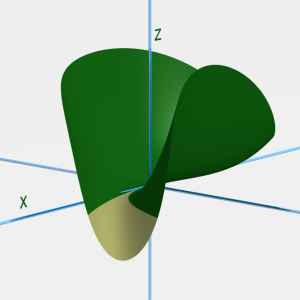
Observez maintenant cette situation.

.

On constate que la zone en jaune, là où on se trouve sous le niveau du point d’équilibre, a une forme très pointue et légèrement tordue. L’équilibre est-il instable ? Ne peut-on imaginer que la bille qui dévale la pente soit en quelque sorte éjectée de la zone jaune par une « force centrifuge » qui la ferait remonter au dessus du point de départ, assurant ainsi une stabilité ?

De nombreux ouvrages de physique affirment, sans démonstration, qu’il ne peut y avoir stabilité que s’il y a minimum. Ont-ils raison ? Dans l’exemple précédent, il serait en effet facile de montrer que l’équilibre est instable et que la bille peut en effet dévaler la pente.

La question se pose donc de la réciproque du théorème de Lagrange-Dirichlet ³Pour être précis, on suppose le potentiel analytique réel et le point d’équilibre isolé. Il a fallu attendre 1977 pour que Palamodov démontre enfin cette réciproque… pour des potentiels qui ne dépendent que de deux variables (\((x,y)\) sur nos figures). Si le potentiel dépend de plus de variables, le même Palamodov affirme avoir démontré le théorème en 1995 mais il n’a publié qu’une esquisse de preuve qui ne semble pas tout à fait convaincre les spécialistes. Selon certains, la réciproque du théorème de Lagrange-Dirichlet serait encore un problème ouvert.

Marco reprend le problème en le plaçant dans un contexte bien plus général, en le libérant en quelque sorte de ses aspects mécaniques. Il s’agit d’équations différentielles.
Considérons un point du plan \((x,y)\) qui évolue au cours du temps en suivant une équation différentielle
\[
\frac{dx}{dt}=-y \quad ; \quad \frac{dy}{dt}=x.
\]
Les solutions de cette équation sont explicites :
\[
x(t) = x(0) \cos t – y(0) \sin t \quad ; \quad y(t) = x(0) \sin t+ y(0) \cos t.
\]
Dans le plan, ce sont des cercles concentriques.
Si la courbe part d’une position initiale proche de l’origine, elle ne s’en éloigne pas. L’origine est une position d’équilibre stable.

Le théorème que je voudrais décrire concerne le cas de la dimension 3. On considère une équation différentielle :
\[
\frac{dx}{dt}= P(x,y,z) \quad ;\quad \quad \frac{dy}{dt}= Q(x,y,z) \quad ; \quad \quad \frac{dz}{dt}= R(x,y,z).
\]
Il faut bien sûr des hypothèses pour un théorème. On suppose que \(P,Q,R\) sont des polynômes qui sont nuls à l’origine \((0,0,0)\). L’origine est alors une position d’équilibre pour l’équation : un point partant de l’origine y reste ! On suppose également que dans un voisinage de l’origine, il n’y a pas d’autre point d’équilibre. Alors le théorème affirme que l’origine est instable ! Cela signifie qu’on peut trouver des points arbitrairement proches de l’origine qui s’en éloignent de manière significative après un certain temps, dans le futur ou dans le passé.
Plus précisément, il établit l’existence d’une position initiale \((x_0,y_0,z_0)\) proche de l’origine (et différente de celle-ci) telle que \((x(t),y(t),z(t))\) tend vers \((0,0,0)\) soit lorsque le temps \(t\) tend vers plus l’infini, soit vers moins l’infini.
On peut présenter les choses autrement. Si un point part de \((x(t),y(t),z(t))\), alors après un temps \(-t\) il se retrouve en \((x_0,y_0,z_0)\). Comme \((x(t),y(t),z(t))\) est arbitrairement proche de l’origine, cela entraîne bien l’instabilité annoncée.

Énoncé simple et preuve élaborée. Le lecteur peut jeter un coup d’œil à cet article.

La même preuve, légèrement adaptée, donne le théorème de Palamodov, c’est-à-dire la réciproque du théorème de Lagrange-Dirichlet {pour les potentiels qui dépendent de deux variables}.

Nous avons vu qu’une équation différentielle peut être stable en dimension 2 et qu’elle est toujours instable en dimension 3.
Qu’en est-il en dimension supérieure ? C’est la conjecture de Brunella : une position d’équilibre isolée d’une équation différentielle polynomiale ⁴En fait la conjecture concerne plus généralement les équations analytiques réelles. en dimension impaire est toujours instable.

C’est l’occasion de commenter l’usage du mot « conjecture ». Il n’est pas rare qu’un mathématicien propose un énoncé qu’il pense vrai mais qu’il ne sait pas démontrer. Parfois, il l’énonce avec force en le baptisant « conjecture ». D’autres fois, de manière plus modeste, il se contente de le présenter comme une simple question. D’autres mathématiciens peuvent ensuite promouvoir l’énoncé au rang de conjecture. C’est ce que je viens de faire avec la conjecture sur les équations différentielles. Marco, avec la sobriété d’écriture qui le caractérisait, se contenta d’une remarque entre parenthèses. Après avoir rappelé le concept de stabilité d’une position d’équilibre, il ajoute dans cette parenthèse qu’il ne connaît aucun exemple en dimension impaire (« we don’t know any »).

Ce n’est qu’un exemple d’un résultat de Marco, parmi tant d’autres.

Sobriété et concision sont les deux mots qui me viennent à l’esprit quand je pense à Marco.