Où l’on apprend qu’un triangle c’est trois carrés qui tournent en rond.
Une histoire du petit prince
Le petit prince a un jour demandé à un peintre qu’il lui dessine un carré. Plusieurs carrés. Un pour chaque couleur que prend sa rose. Il les a étalés devant lui et s’est mis à jouer avec. Il a rêvé d’en faire un kaléidoscope et a commencé à les épingler deux à deux. Il a fait en sorte que chaque coin de ses carrés soit épinglé avec le coin d’un autre carré.
L’aviateur qui le regardait imaginait que c’était autant d’hélices multicolores. Il s’est alors demandé combien il faudrait de carrés au petit prince pour accomplir son rêve coloré. Il a commencé par faire un patchwork, comme un damier.
.
Mais d’une part les quatre coins du damier n’étaient pas épinglés et d’autre part c’était bien trop rigide : à l’intérieur du damier les coins étaient épinglés 4 par 4 et deux carrés adjacents étaient épinglés par deux fois ensemble …
Alors, comment faire ? Comment placer des carrés, tous identiques à l’exception de la couleur, sur la table, en les superposant si nécessaire, de sorte que n’importe quel coin d’un carré soit épinglé avec le sommet d’un autre carré. Oui, absolument tous les coins doivent être appariés ! Et si possible en faisant en sorte que deux carrés aient au plus un seul coin d’épinglé ensemble et qu’une épingle ne serve que pour deux carrés.
Le mathématicien
J’ai posé cette question à de nombreuses personnes, mathématiciennes ou non.
Les mathématicien-ne-s m’ont souvent demandé de préciser mon énoncé. Par exemple : qu’est-ce qu’un carré ? Voici donc une formulation plus précise !
On appelle carré un ensemble de quatre points du plan formant un carré de côté 1. On cherche un ensemble (fini) de carrés \(C_1\), \(C_2\), … , \(C_n\) de telle sorte que :
– pour tout sommet d’un carré \(C_i\), il existe exactement un autre carré \(C_j\) dont c’est également le sommet ;
– deux carrés \(C_i\) et \(C_j\) distincts ont au plus un sommet commun.
Le premier mathématicien à qui j’ai posé cette question a cherché à refermer le damier en le tordant, en faisant tourner une ligne de carrés. Au bout de quelque temps il a fini par trouver une jolie solution, avec plein de belles propriétés géométriques. Pour l’apprécier, le mieux est de chercher soi-même !
Pour les impatient-e-s, la voici !
On dessine un hexagone dont chaque côté est de longueur 1. À partir de chacun de ses côtés, sur le bord on dessine un carré, vers l’extérieur de la figure. On obtient une sorte de roue (dentée). Les dents sont à distance exactement 1. Par conséquent si on prend une seconde roue et qu’on la tourne légèrement (de 30 degrés), elle s’intercale parfaitement ! Chaque sommet sur le bord d’un hexagone est commun à deux carrés sur une même roue, tandis que les autres sommets se correspondent d’une roue sur l’autre.
.
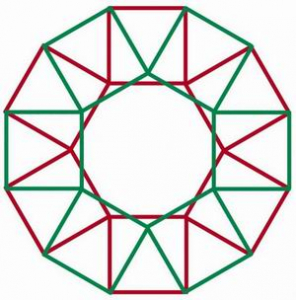
La mathématicienne
Quand j’ai appris à mon collègue que je connaissais une solution avec encore moins de carrés, il ne m’a pas cru. Puis il a cherché et a fini par en trouver une. Elle avait bien moins de symétries et moins de jolies propriétés géométriques. Mais elle était belle. Nous l’avons interprété comme un objet de la quatrième dimension !
Mais j’avais posé la question à d’autres personnes. L’une d’elle n’est pas du tout mathématicienne. Elle a cherché à ses heures perdues au bureau (elle est secrétaire) avec des post-it. Excellente idée ! Et elle a trouvé une figure géométrique bien plus simple, avec le même nombre de carrés. J’ai découvert cette figure avec stupéfaction : j’étais persuadé que l’interprétation avec un objet de la quatrième dimension était la meilleure et qu’il n’existait aucune figure géométrique plane permettant de comprendre cette configuration. Et pourtant, et pourtant …
Ce fut, à nouveau, une belle démonstration de science populaire. En partageant ce problème, et bien que je fus en ce regard l’expert, c’est moi qui ai appris : point de transmission verticale d’un savoir, point de miettes que l’on condescend à divulguer … mais un partage ! Et si j’ai parlé de quatrième dimension, de tesseract ou d’octochore à mon amie, c’est bien elle qui m’a appris une bien jolie propriété d’un des figures planes les plus simples !
Je vous propose de ne regarder ce qui se cache en dessous que si vous avez découvert la solution précédente et avez cherché une solution avec 4 carrés de moins !
Mon interprétation de la figure est celle de la projection d’un hypercube (un cube de dimension 4) sur un plan. Dans cette interprétation, il est clair qu’on peut déformer la figure et c’est pourquoi je la trouve bonne, mais on rate quelque chose en disant cela.
Je vais d’abord vous présenter ma solution. Même si vous ne savez peut-être pas ce qu’est un hypercube, admettez une seconde que c’est le produit de deux carrés. Bien sûr je devrais vous expliquer ce que ça veut dire … mais un prochain article du café des maths le fera. Disons que si on prend deux segments perpendiculaires l’un à l’autre, on fabrique un carré.
.
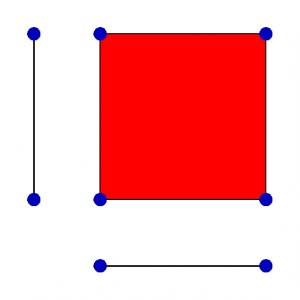
Si l’on avait pris un second segment non perpendiculaire au premier, on aurait obtenu un parallélogramme. Ce qui veut dire qu’on peut faire bouger un parallélogramme, le déformer. En un autre parallélogramme, et même en rectangle. Vous le savez bien, c’est comme une étagère ! Sans croisillons, elle se déforme. On aimerait que ce soit un rectangle posé sur le sol, mais ça fait souvent un machin de guingois. Les matheu-se-s disent qu’un parallélogramme est flexible, déformable.
De même avec un carré et un segment, on fabrique un cube. Si on ne les met pas perpendiculairement, on a en fait un parallélépipède. Eux aussi sont flexible, déformables !
Bon, vous êtes prêt-e-s pour la quatrième dimension !
Avec deux carrés, on fabrique un hypercube, ou tesseract … un cube de dimension 4 : prenez le produit de deux carrés, A et B, perpendiculaires et ayant un sommet commun ! Évidemment dans l’espace habituel ce n’est pas possible. Mais si on accepte la quatrième dimension, c’est possible. Pour le voir autrement, imaginez que votre deuxième carré (B) est un produit de deux segments (C et D). On prend le produit du carré A avec C, on obtient un cube. Un joli cube dans l’espace habituel, que l’on appellera AxC. Maintenant disons que D est un segment mais dans le temps, une demie-heure par exemple : D est le segment qui va de midi à midi et demie. Qu’est-ce que le produit du cube AxC par D ? C’est le cube AxC est filmé entre midi et midi et demie ! Pour le voir, il faut regarder un film (pas très animé) pendant une demie-heure !
Un hypercube est donc encore une fois quelque chose de très déformable, de très flexible, et de dimension 4. Les joueurs et joueuses se souviennent peut-être d’aventures jouées dans la hutte de Baba Yaga ! Elle avait la forme d’un tesseract ?
.
Si l’on projette cet objet dans le plan (pour en faire une photo), on obtient plein de figures possibles. Tout comme on peut photographier un objet en 3D de plein de façons différentes, selon l’angle de vue. La plus connue est celle de deux cubes reliés entre eux : c’est mon image du film. Les deux cubes sont les positions à midi et midi et demie, les traits qui les relient sont les instants entre midi et midi et demie.
.
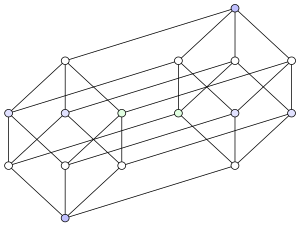
Il y en a d’autres plus jolies, un peu comme des fleurs :
.
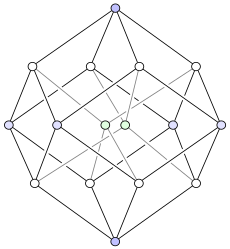
Mais il y en a une très simple, celle du produit de tout à l’heure ! On dessine un carré A et un carré B ayant un sommet commun avec A, mais on dessine tout ça sur une feuille de papier ! Pas dans la quatrième dimension … On dessine ensuite en tout sommet de A une copie de B et pareil, en tous sommets de B une copie de A. Cette figure est flexible ! Bien entendu ! B peut-être en fait n’importe quel carré faisant un angle quelconque avec le premier carré A !
.
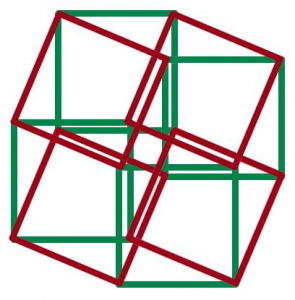
Voilà, ça c’était ma solution !
Mais mon amie a remarqué que si on fait faire un angle de 45 degrés entre A et B, on obtient un … octogone ! Eh oui ! Ce qui est bien naturel puisque l’autre nom de l’hypercube, hormis tesseract, c’est octochore !
Voici ce bel octogone 2Les dessins de ce bloc dépliant proviennent de wikipedia, à l’exception du premier qui provient d’un article d’Étienne Ghys, de l’avant-dernier que j’ai réalisé et du dernier qui a été réalisé (après la version post-it) par Isabelle, mon amie géomètre qui s’ignore !.
.
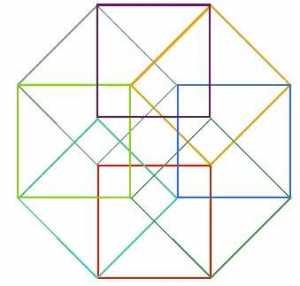
Je pense que vous êtes d’accord avec moi pour dire que mon amie est une mathématicienne, n’est-ce pas !
Un triangle c’est trois carrés qui tournent en rond !
J’ai également posé la question au jury de l’agrégation (aux membres du jury, pas aux candidat-e-s, rassurez-vous !). L’une des professeures présentes s’est entichée du problème et il nous arrive d’en discuter devant nos collègues. Et pourquoi ? Parce que même si nous sommes ravi-e-s de cette belle solution, même si nous sommes convaincu-e-s qu’il n’y en a pas de meilleure … encore faut-il le démontrer !
Ce site doit vous avoir convaincu-e qu’en mathématique on n’est pleinement satisfait-e que si on sait pour sûr qu’on ne peut pas faire mieux. Il ne s’agit pas de le deviner, d’en être intimement convaincu-e, mais de démontrer que ce n’est pas parce qu’on a raté quelque chose qu’on n’y arrive pas !
Alors, je ne vois pas comment faire une jolie figure pour le petit prince avec moins de carrés, mais est-ce que vraiment il n’en existe pas ? Je ne suis pas encore complètement sûr, bien que j’aie écrit une démonstration … c’est que je ne l’ai pas encore vraiment décortiquée et que je ne l’ai pas non plus montrée à ma collègue !
Voici le principe. On remplace les carrés par des points, que l’on appellent sommets. On joint ces sommets par des traits, appelés arêtes, si les deux carrés correspondant ont un sommet commun. L’ensemble formé par les sommets et les arêtes que nous venons de construire s’appelle un graphe.
Comme chaque carré a quatre coins qu’il partagent avec quatre autres carrés, de chaque sommet partent quatre arêtes. On dit que tout sommet est d’ordre 4.
Puisqu’il y a un sommet et quatre arêtes aboutissant à quatre autres sommets, c’est qu’on a au moins cinq sommets. Autrement dit la figure doit comporter au moins 5 carrés.
On voit facilement que si le graphe ne comporte aucun triangle, alors il a au moins 8 sommets. Mieux ! Dans ce cas c’est un graphe bi-partite : on peut séparer ses 8 sommets en deux paquets de 4 et chacun des éléments d’un des deux paquets est relié par une arête à tous les éléments de l’autre paquet, mais à aucun de son propre paquet.
Une telle configuration de carrés existe !
Si maintenant on a un seul triangle … mais au fait c’est quoi un triangle ?!
C’est la question que nous nous sommes posé avec ma collègue, alors que nous partions déjeuner avec d’autres membres du jury. La réponse vint toute seule : ben, un triangle, c’est trois carrés qui tournent en rond !
Rassurez-vous nos collègues aussi nous ont regardé de travers … et nous avons explosé de rire après avoir dit cela ! Et pourtant, et pourtant c’est bien ce que signifie cette configuration : ce sont trois carrés qui ont un sommet commun deux à deux, ils tournent donc autour d’un triangle en quelque sorte.
Ainsi, on peut voir que si un triangle n’a pas de côté commun avec deux autres triangles au moins, alors il a encore au moins huit sommets. Pour faire mieux, il faut donc que tout triangle ait au moins un côté de commun avec deux autres triangles. Je vous laisse terminer … mais je vous préviens ce n’est pas ce que l’on pourrait appeler un problème facile !
ÉCRIT PAR
François Sauvageot
Professeur - Lycée Alain-René Lesage - Académie de Rennes
