Le séminaire de la semaine dernière : les systèmes dynamiques stablement ergodiques

Dans mon premier billet, je vous avais promis, chaque mois, de raconter un des derniers exposés auxquels j’ai assisté (d’où le titre de la série de billets : « Le séminaire de la semaine dernière »). Pour ce deuxième billet, je triche déjà (un peu) : je vais vous parler d’un exposé qui date d’il y a presque 3 mois ! (j’ai plein de mauvaises excuses, que je n’ose même pas vous présenter). Il s’agit d’un exposé que Martin Andersson a donné en novembre à Orsay. Il parlait de « systèmes dynamiques stablement ergodiques ».

Un exemple

Pour vous donner une idée de ce dont il s’agit, commençons par une sorte de jeu. a) On part d’un carré, qu’on a colorié avec un dégradé du bleu au rouge (ci-dessous, à gauche). b) On étire verticalement ce carré, jusqu’à avoir obtenu un rectangle deux fois plus haut et deux fois moins large que le carré initial. c) On coupe le rectangle obtenu à mi-hauteur. d)On prend le morceau supérieur, et on le déplace pour l’amener à droite du morceau du bas. e) On colle les deux morceaux, afin d’obtenir un carré (ci-dessous, à droite) de mêmes dimensions que le carré initial.

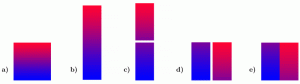
Bien sûr, dans le carré obtenu à droite, la disposition des couleurs n’est plus la même que dans le carré initial : on a maintenant deux bandes verticales ; dans celle de gauche, la couleur varie du bleu au violet, dans celle de droite, la couleur varie du violet au rouge.

On peut alors faire subir au carré obtenu ci-dessus à droite le même sort que celui qu’on a fait subir au carré initial. a) On part du carré obtenu ci-dessus à droite. b) On étire verticalement. c) On coupe à mi-hauteur. d) On déplace le morceau du haut. e) On colle les deux morceaux.

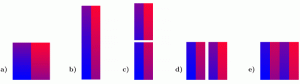
On obient un nouveau carré avec quatre bandes de couleurs verticales… auquel on peut faire subir le même sort qu’aux carrés précédents : on étire, on coupe, on déplace, on colle… On obtiendra un nouveau carré avec huit bandes de couleurs verticales… auquel on pourra faire subir le même sort qu’aux carrés précédents… et ainsi de suite. Voici le carré qu’on obtient après avoir appliqué le procédé quatre fois de suite :

… et le carré qu’on obtient après avoir appliqué le procédé neuf fois de suite :

Vu de loin il n’y a plus de zone rouge, ni de zone bleue dans notre carré ; tout semble plus ou moins violet. Bien sûr, les pixels rouges et les pixels bleus n’ont pas disparu ; mais ils sont répartis un peu partout dans le carré et intimement mélangés les uns aux autres. La couleur de chaque partie du carré est donc un mélange de bleu et de rouge, d’où ce violet à peu près uniforme.

Mathématiquement, on peut rendre compte du phénomène de « mélange des pixels bleus, violets et rouges » de la manière suivante : la transformation du carré considérée (étirer, couper, déplacer, coller) ne laisse à sa place aucune partie du carré, aussi petite soit-elle ⁶Plus précisément, pour les lecteurs savants : les seules parties du carré qui sont laissées invariantes par la transformation sont de mesure de Lebesgue nulle, ou ont un complémentaire de mesure de Lebesgue nulle. Une transformation qui vérifie cette propriété est dite ergodique.

En fait, la transformation du carré considérée ci-dessus vérifie une propriété supplémentaire. Supposons qu’on modifie un peu cette transformation ; par exemple, au lieu d’étirer le carré en un rectangle vertical bien droit, on « fait mal le travail », et on se retrouve avec un rectangle un peu tordu… puis on coupe ce rectangle tordu à mi-hauteur, on déplace le morceau du haut, etc. On peut montrer que cette transformation un peu modifiée est encore ergodique. C’est pourquoi, on dit que la transformation initiale est stablement ergodique.

Remarque. Ce phénomène de « mélange des couleurs » vous rappelle peut-être votre enfance. Un beau matin d’hiver, votre maman vous achetait une dizaine de bâtons de pâte à modeler de toutes les couleurs de l’arc-en-ciel. Vous étiriez certains bâtons, en aplatissiez d’autres, découpiez des morceaux, assembliez le tout pour donner naissance à quelque bonhomme… puis ce premier personnage était écrabouillé pour servir de matière à la confection d’un autre, etc. Et à la fin de l’après-midi, il ne restait plus qu’une grosse boule de pâte à modeler d’une affreuse couleur vaguement « grisâtro-marronnasse » … (c’est une des plus grandes frustrations de mon enfance).

Il y a cependant une différence importante entre votre enfance, et la transformation du carré que j’ai décrite ci-dessus. Dans le cas de la pâte à modeler, on peut penser que le mélange des couleurs provient du caractère aléatoire (ou du moins irrégulier) des transformations qu’applique l’enfant (celui-ci n’étale pas les bâtons toujours de la même manière, ne coupe pas toujours au même endroit, n’écrabouille pas toujours avec la même conviction…). Mais dans l’exemple ci-dessus, on applique à chaque fois la même transformation au carré (on étire toujours de la même façon, on coupe toujours au même endroit, etc.). Neuf applications successives de la même transformation très simple suffisent à mélanger les couleurs.

 

Un mot du travail d’Andersson

Pourquoi la transformation du carré décrite ci-dessus est-elle ergodique ? Moins formellement : pourquoi, en quelques applications successives, cette transformation mélange-t-elle complètement les points de couleurs bleue et rouge ? Si on réfléchit un peu, on se rend compte que cela provient du fait que cette transformation « étire le carré dans la direction verticale ». En effet, supposons qu’on ait deux points du carré initial, très proches, mais pas situés exactement à la même hauteur. Comme ces deux points sont très proches, ils sont pratiquement de la même couleur. Quand on applique la transformation, on commence par étirer le carré verticalement en un rectangle deux fois plus haut. La différence de hauteur entre nos deux points se trouve ainsi mutlipliée par deux. À l’étape suivante, elle est à nouveau multipliée par deux. Etc. Ainsi, après quelques applications successives de la transformation, nos deux points seront situés à des hauteurs complètement différentes, et donc à des endroits complètement différents du carré. C’est ainsi qu’on se retrouve avec des points bleus, des points rouges et des points violets répartis un peu partout dans le carré.

Dans son exposé, Martin Andersson présentait ses résultats récents, qui, combinés à ceux d’autres chercheurs (Ali Tahzibi ⁷Au passage, je vous invite à jeter un oeil à un article sur le blog de Sylvestre Huet, qui raconte comment Ali Tahzibi, professeur associé dans une université brésilienne, s’est vu refuser un
visa pour un séjour de recherche d’une année en France. Triste époque…, Jairo Bochi, Bassam Fayad, Enrique Pujals, entre autres), permettent presque de caractériser les transformations stablement ergodiques. Ici, on ne s’intéresse pas aux seules transformations du carré ; on considère les transformations d’un espace quelconque, avec un nombre arbitraire de dimensions. Et les transformations considérées n’admettent pas nécessairement une description géométrique simple comme c’était le cas pour la transformation du carré ci-dessus. En simplifiant très grossièrement, les travaux d’Andersson et des autres chercheurs du domaines tendent à montrer que « les transformations stablement ergodiques sont celles qui étirent certaines directions et contractent les autres ».

Bien sûr, il faudrait préciser le sens de l’expression « étirer certaines directions » (la transformation étire-t-elle partout de la même manière ? ou bien étire-t-elle seulement « en moyenne » ? etc.)… mais je préfère essayer de vous expliquer pourquoi certains mathématiciens s’intéressent aux transformations stablement ergodiques.

Pourquoi des mathématiciens s’intéressent-ils à cela ?

L’évolution des orbites de planètes qui gravitent autour d’une étoile sous l’effet de l’attraction universelle, l’évolution d’un écosystème constitué de populations animales et végétales qui interagissent entre elles, l’évolution des concentrations d’espèces chimiques au cours d’une réaction sont trois phénomènes a priori très différents, mais qui peuvent être modélisés par le même genre d’objet mathématique. En fait, il s’agit de trois exemples de systèmes dynamiques. Un système dynamique (à temps discret) est la donnée :

• d’un espace des états : c’est un ensemble dont les points représentent les états possibles du système. Dans le premier exemple ci-dessus, il s’agit de l’ensemble des positions et des vitesses possibles pour les planètes considérées.
• d’une loi d’évolution ; c’est une transformation de l’espace des états qui décrit dans quel état sera le système à l’instant \(t+1\) en fonction de son état à l’instant \(t\). Par exemple, la loi d’évolution la plus simple pour un écosystème est celle où les populations à l’instant \(t+1\) sont proportionnelles à celles de l’instant \(t\)⁸La croissance des populations est alors exponentielle. C’est par exemple ce qui se passe au début d’une invasion bactérienne..

Abstraitement, n’importe quel ensemble (par exemple, un carré) peut être vu comme l’espace des états d’un système dynamique, et n’importe quelle transformation de cet ensemble (par exemple, la transformation du carré décrite au début du billet) peut être vue comme la loi d’évolution de ce système dynamique. ⁹Bien sûr, c’est une opération purement formelle : le système dynamique obtenu ne modélise a priori aucun phénomème physique, écologique, biologique, ou chimique particulier.

Un vaste problème mathématique consiste à prédire l’évolution à long terme d’un système dynamique, connaissant sa loi d’évolution. La diversité des exemples décrits ci-dessus montre bien que ce problème ne peut admettre une réponse universelle : certains systèmes dynamiques tendent rapidement vers un état d’équilibre, d’autres ont un comportement périodique, d’autres ont une évolution si compliquée qu’elle semble gouvernée par le hasard (on parle de comportement chaotique) ¹⁰Dans quelques jours, paraîtra sur ce site un magnifique article d’Etienne Ghys et Jos Leys, en hommage au travail d’Edward Lorenz, où vous pourrez voir des exemples concrets de systèmes dynamiques qui tendent vers un état d’équilibre, ont un comportement périodique, ou ont un comportement chaotique. Un peu de patience…. Pour attaquer un problème aussi vaste, une stratégie naturelle consiste à étudier les systèmes qui ont un comportement paradigmatique ; ainsi, on s’intéresse aux systèmes stablement ergodiques car ce sont, en quelque sorte, les systèmes dynamiques qui ont le comportement « le plus parfaitement compliqué possible ». En étudiant les systèmes stablement ergodiques, les mathématiciens espèrent plus généralement comprendre quels sont les mécanismes qui conduisent à l’apparition d’un comportement compliqué dans un système dynamique.