Le similéidoscope

Récemment, nous nous sommes pris à jouer longuement avec le gadget qui fait l’objet de ce billet. C’était inattendu pour nous dans la mesure où le jeu a commencé au cours d’un groupe de travail très sérieux ⁴Il s’agissait d’étudier les « variétés affine plates »..

 

Le dernier jouet de notre séminaire de géométrie

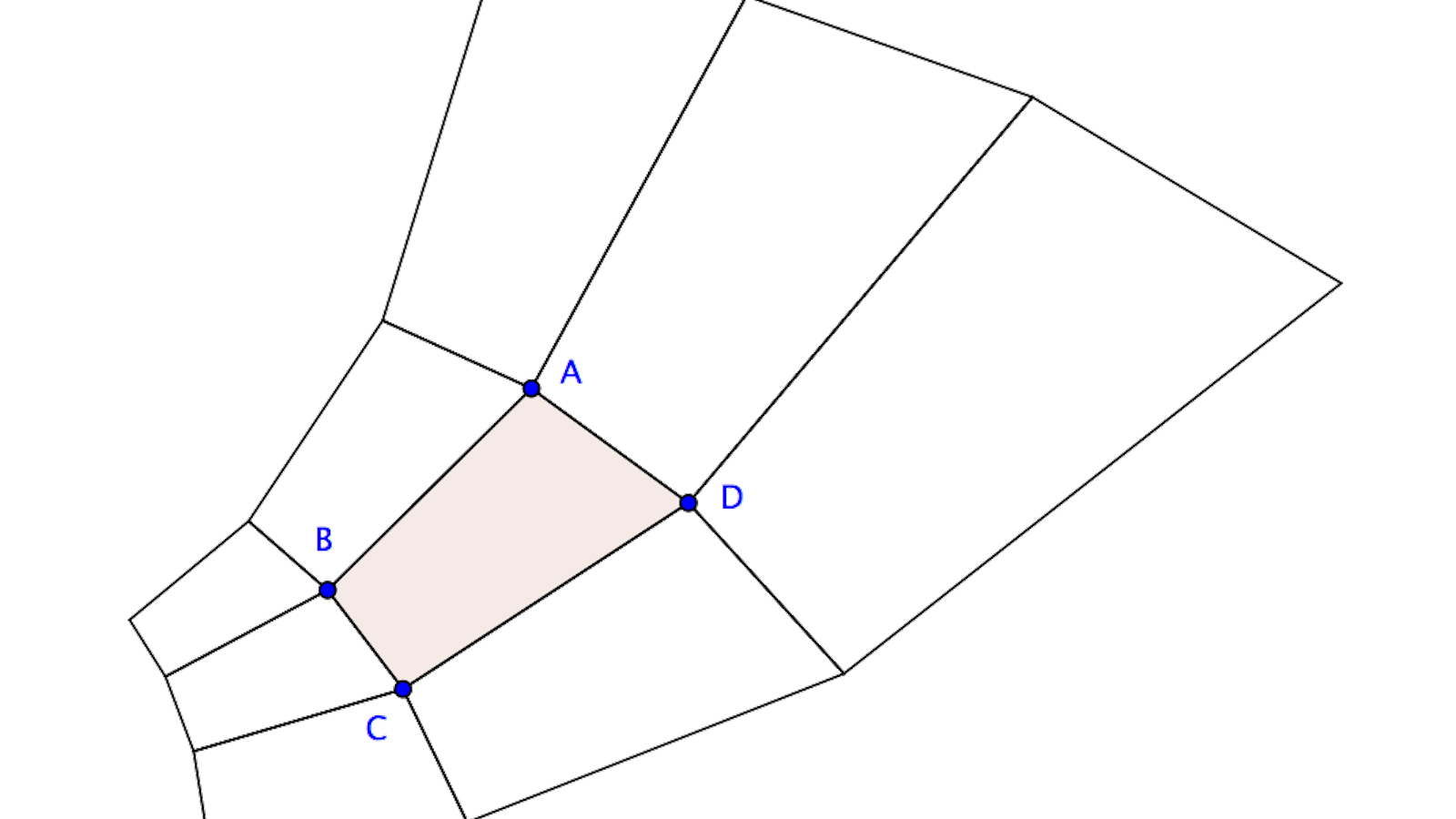
Le jouet consiste en la figure qui suit. Vous y verrez quatre points marqués A, B, C et D, qui sont les sommets d’un quadrilatère que nous notons Q, quadrilatère qui est un pavé d’un pavage d’une région plus grande, ou si vous préférez qui est une maille d’un morceau de toile d’araignée. En cliquant sur l’un de ces quatre sommets et en le déplaçant avec votre souris, vous aller déformer Q, et observer que la déformation se propage du même coup à toute la portion dessinée de la toile d’araignée. Nous avons trouvé cela amusant, et aussi fascinant, un peu comme un kaléidoscope — et nous espérons ne pas être les seuls.

Un peu de géométrie plane

Mais qu’y a-t-il là-dessous ? Rappelons d’abord ce qu’est une similitude du plan. Une première définition : une similitude est une transformation du plan qui conserve les rapports de longueurs ; il en résulte qu’elle conserve aussi les angles. Ainsi, dans une image de ma feuille de papier par une similitude, je ne peux pas reconnaître la largeur et la hauteur de la feuille, mais je peux voir quel est le rapport hauteur/largeur ; pour une feuille A4 (ou d’ailleurs A5, ou A3), le rapport hauteur/largeur est à peu près 1,41, et plus précisément \(\sqrt2\)) ; et une similitude directe est une similitude telle que l’image d’une main droite est encore une main droite (et non une main gauche).

Une seconde définition, qu’on montre en géométrie plane être équivalente à la première : une similitude directe est ou bien une translation (déterminée par sa direction et son amplitude), ou bien une rotation (déterminée par son centre et son angle de rotation), ou bien une homothétie (déterminée par son centre et son rapport, disons r, et transformant toute figure en une figure r fois plus grande), ou bien la composition d’une rotation et d’une homothétie de même centre. Sur l’image précédente, la rotation est de 60° (autour du point noté O) et le rapport r vaut 1/2.

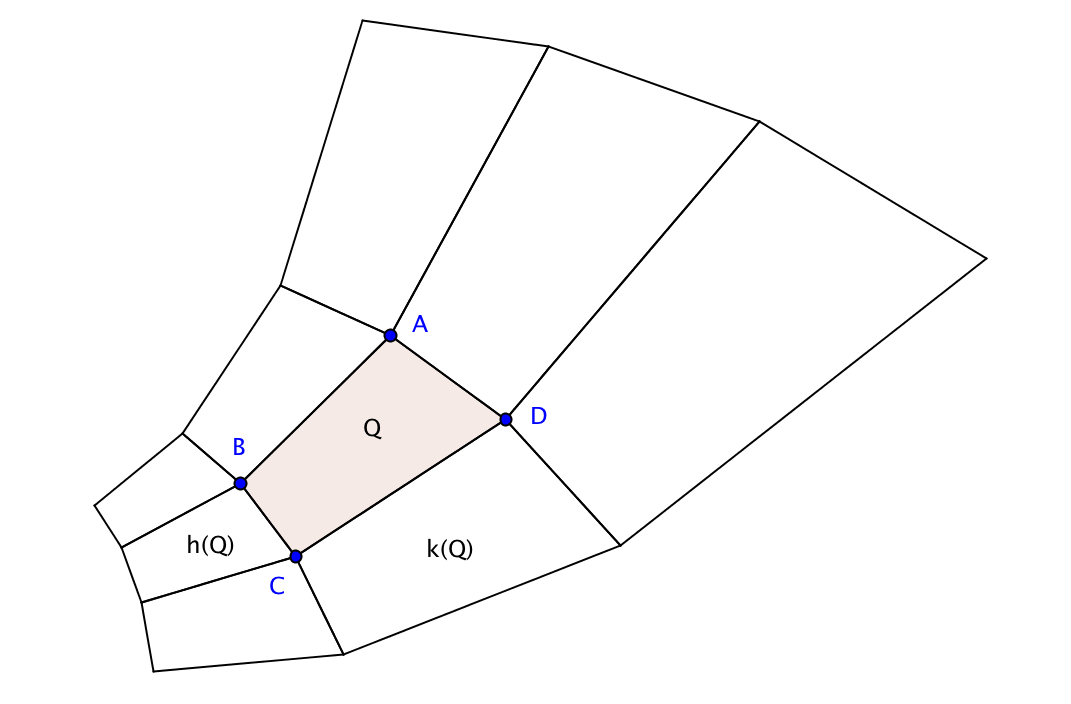
Et voici la propriété essentielle pour notre jouet : étant donné un quadrilatère Q de sommets A, B, C et D, il existe d’une part une unique similitude directe h qui transforme le côté orienté AD en le côté orienté opposé BC de Q, et d’autre part une unique similitude directe k qui transforme le côté orienté AB en le côté orienté DC. L’image h(Q) du quadrilatère Q est un autre quadrilatère, parfaitement déterminé, qui s’ajuste au premier le long du côté BC, et de même k(Q) est encore un quadrilatère qui s’ajuste au premier le long du côté DC. En considérant les transformations inverses de h et k, on obtient des quadrilatères images de Q qui s’ajustent le long des autres côtés. Et on peut recommencer plusieurs fois, pour paver un morceau du plan avec des images de Q ; pour comprendre le processus d’itération, il est bon de réaliser que h et k commutent, et en particulier que h(k(Q)) = k(h(Q).

Voici par exemple l’image obtenue avec les 8 quadrilatères qui touchent Q, dont quatre le touchent le long d’un côté (les images de Q par h, k, et leurs inverses) et les quatre autres le touchent en un seul sommet (les images de Q par hk, hk\(^{-1}\), h\(^{-1}\)k et h\(^{-1}\)k\(^{-1}\)).

 

Quelques questions

On peut évidemment se poser une foule de questions : pourquoi les quadrilatères suivants s’ajustent-ils si bien ? dans quelles situations et à partir de quand en viennent-ils à se superposer les uns sur les autres ? si la situation où Q est un rectangle est manifestement très spéciale, y a-t-il d’autres situations spéciales ? est-il important que le quadrilatère Q soit convexe, c’est-à-dire sans angle plus grand que 180 degrés ? que se passe-t-il quand Q cesse d’être simple ? (avec deux côtés qui se coupent), etc, etc, etc !

Précisons que l’idée n’est pas de nous, mais (autant que nous sachions) de John Smillie, et qu’elle apparaît dans les textes des grands maîtres⁵Voir le cours de Thurston de la fin des années 1970, et en particulier la page 37 de ce livre disponible en version électronique. . Pour aujourd’hui, nous vous proposons simplement de jouer.

Le logiciel

Encore un mot sur GeoGebra ⁶Voir http://www.geogebra.org/cms/fr, le magnifique logiciel de géométrie plane qui nous a permis d’obtenir les figures souhaitées et de les animer. Il contient des outils déjà définis, comme la création de droites parallèles, ou de points d’intersection, ou d’images de points par une rotation, etc. A partir de ces outils de base, on peut en créer d’autres ; par exemple, étant donné un quadrilatère Q et une paire de côtés opposés de Q, la similitude directe h qui transforme le premier côté de la paire en le second, et on peut en prime faire dessiner h(Q).

GeoGebra vous permet de jouer à créer d’autres images montrant Q et son réseau courtisan. Voici par exemple une figure où Q est tel que toutes ses images recouvrent exactement et sans chevauchement le plan privé d’un point.

Ou encore une autre, où les images de Q recouvrent également le plan privé d’un point, mais se chevauchent les unes les autres.

Pour comprendre la différence entre cette figure et la précédente, tournez autour du point central en partant de AB. Dans la première figure, on obtient un contour fermé qui est un pentagone ; dans la seconde, on retraverse une fois Q et on continue à spiraler vers le point central.

Pour terminer, voici un exercice d’habileté un peu délicat que nous proposons au lecteur : en plaçant convenablement les points A, B, C et D sur l’animation GeoGebra et reproduite au début de ce billet, retrouver les deux dernières figures, ainsi que leurs analogues pour des structures à 6 ou 7 rayons autour du point central (au lieu de 5 ci-dessus).