L’enseignement des mathématiques

Toujours dans le désarroi et la tourmente !

Les problèmes de l’enseignement des maths sont toujours là et ne cessent de hanter les responsables, constamment inquiets par la publication des enquêtes successives sur le sujet, en particulier celles de PISA (Programme for International Student Assessment) et du TIMSS (Trends in International Mathematics and Science Study). Chaque gouvernement fraîchement élu promet de les éradiquer en mettant en place des commissions de réflexion, en lançant des initiatives… Mais après les premiers remous et quelques gesticulations, les bonnes volontés s’estompent et sont renvoyées aux calendes grecques. Rien n’a jamais réellement bougé ! Espérons que la mission confiée dernièrement à Charles Torossian et Cédric Villani – qui ont rendu récemment leur rapport avec dedans leurs vingt et une mesures – aboutira à quelque chose.

Mais ce qui est tout de même curieux, c’est qu’on ne dit jamais comment ces problèmes sont nés ni comment ils ont été cultivés depuis lors !

La situation a commencé à se dégrader il y a presque trente ans, quand des politiques zélés, pensant sans doute bien faire, ont dénoncé ce qu’ils qualifiaient de « domination des maths, leur côté matière de sélection… » Le plus désolant est que ceci, bâti souvent sur une méconnaissance de la discipline, a trouvé – et trouve encore à nos jours – écho auprès de beaucoup de monde : ceux dont les enfants n’arrivent pas à franchir un cap « à cause » des maths (disent-ils !), ceux qui en gardent de mauvais souvenirs, ceux qui les détestent ou qui avaient un contact difficile avec l’enseignant… moult raisons qui font qu’ils n’hésitent pas à porter main forte à tous ceux qui profèrent ces récriminations. Il n’est pas rare d’entendre certains répéter (avec fierté !) des « J’étais nul en maths ! », « Je n’aimais pas les maths ! », « J’avais un mauvais prof ! »… Cet acharnement s’est amplifié et a été relayé par les médias. Voici par exemple ce qu’on pouvait lire en 2006 :

Ce n’était donc pas si étonnant qu’une masse de gens ait accepté cette idée de « dictature des maths », soutenue par des décideurs, qui ont même promis en passant, et de façon quelque peu démagogique, de relever très haut le taux de réussite au baccalauréat. Comment est-il possible de faire cela si ce n’est en baissant drastiquement le niveau des enseignements, et en particulier celui des maths qui passe pour être le catalyseur de tous les maux ? (Mais on y est arrivé quand même : ce tauxa failli atteindre les 80% en 2017! Reste à voir ce que va donner la nouvelle réforme de ce diplôme au niveau de l’enseignement des sciences en général. Personnellement, elle me laisse sceptique!)

Alors pour ce faire, on a commencé à taillader les maths (à tous les niveaux), les alléger, les vider de leur substance, c’est-à-dire le raisonnement et la réflexion qui sont non seulement leurs piliers mais
aussi le but même de leur enseignement… Place aux recettes que les élèves n’ont qu’à mémoriser et à appliquer directement. Des notions ont disparu presque entièrement, par exemple des bribes de certains thèmes ont ravi une bonne part de la place qu’occupait la géométrie qui est la colonne vertébrale des mathématiques et par laquelle on apprend le plus (tout le monde le sait) à mener un raisonnement qualitatif sans toujours être obligé de faire appel à un mécanisme calculatoire.

Beaucoup des élèves ayant subi cette « réforme à reculons » sont aujourd’hui des enseignants ou en passe de le devenir. Et le constat est sans appel : faiblesse du niveau et surtout manque de compétence, de recul, de capacité de réflexion… en somme de tout ce qui est indispensable à celui dont le métier est de transmettre ce savoir à des apprentis.

Le problème de l’enseignement des mathématiques est essentiellement celui-là!

Et on n’est pas prêt à le résoudre: il se posera encore durant plusieurs des années qui viennent. Actuellement on ne peut que le colmater pour en sauver une partie tout en réfléchissant sérieusement à une vraie stratégie pour la suite : il faut sûrement plus de vingt ans pour que la situation regagne sa «normalité.»

Le professorat des écoles

C’est à l’école primaire que débute l’enseignement des maths et c’est là aussi qu’apparaissent ses premières difficultés. Une attention spéciale doit donc être portée à la formation des maîtres, surtout que près de 70~% des »élèves PE » viennent de branches littéraires où la discipline en question est souvent perçue, pour diverses raisons, tout à fait secondaire. Les étudiants eux-mêmes n’y prêtent pas beaucoup d’intérêt, les intégrant en pensant au départ qu’ils ne s’orienteraient jamais vers une carrière d’enseignant du primaire. C’est actuellement l’offre de postes et le nombre faible de candidats qui les y attirent. D’un autre côté, leurs difficultés en maths sont mesurablement au moins les mêmes que celles des étudiants des branches scientifiques en français, matière aussi importante car elle est l’outil principal qui permet la communication aussi bien à l’oral qu’à l’écrit. Je pense que dans cette direction une des solutions est là :

Cette idée n’est pas nouvelle, elle est apparue il y a quelques années ; il me semble que des universités l’ont même déjà mise à l’essai et certaines la pratiquent encore (et si je ne me trompe pas, une Licence assez proche est ouverte au Département des Sciences de l’Éducation à l’Université Charles de Gaulle à Lille). Mais la fameuse réforme qui a rallongé inutilement d’un an toutes les préparations au métier d’enseignant en créant le Master enseignement a stoppé net ce genre d’initiative. C’est une piste sérieuse qui mérite d’être retracée. Je me réjouis de découvrir qu’elle est aussi la première mesure proposée par Charles Torossian et Cédric Villani :

1. Formation initiale. Construire, dès 2018, la formation initiale des professeurs des écoles démarrant à Bac+1, de façon à assurer, dans une licence adaptée ou un parcours pluridisciplinaire, un volume suffisant d’enseignements dédié aux disciplines fondamentales.

C’est une bonne chose que ceci apparaisse aussi dans le dit rapport : les mesures 14, 15 et 16.

14. Référent mathématiques. Développer la formation continue en mathématiques des professeurs des écoles. Dans chaque circonscription, favoriser le développement professionnel entre pairs et en équipe, et nommer un troisième conseiller pédagogique, « référent mathématiques ».

15. Développement professionnel en équipe. Développer la formation continue des professeurs de mathématiques à l’échelle locale, dans une logique de confiance, entre pairs et en équipe ; promouvoir l’observation conjointe ; dégager un temps commun dans les emplois du temps ; identifier les personnes ressources.

16. Laboratoire de mathématiques. Expérimenter, financer et évaluer sous trois ans, dès septembre 2018, dans au moins cinq établissements et un campus des métiers par académie, la mise en place de laboratoires de mathématiques en lien avec l’enseignement supérieur et conçus comme autant de lieux de formation et de réflexion (disciplinaire, didactique et pédagogique) des équipes.

Les laboratoires de mathématiques existent déjà par-ci par-là. Nous (François Recher, Valerio Vassallo et moi) avons participé à leur création dans des établissements des Hauts-de-France et les avons expérimentés, depuis des années, dans le cadre des activités que nous avons menées à la Cité des Géométries (Val de Sambre) et à l’École de la Deuxième Chance du Grand Hainaut. (Nous avons relaté certaines séances de travail : voir par exemple ici ou là.)

Le professorat du secondaire

Les difficultés ne sont pas les mêmes bien qu’elles soient drainées par celles que trimbalent les élèves depuis l’école primaire. Et là encore il y a un vrai problème chez beaucoup d’enseignants recrutés ces dernières années : leur qualification au niveau des connaissances mathématiques et des méthodes d’enseignement n’est pas celle qu’il faut vraiment. Si depuis deux ans les contenus des programmes de la préparation au CAPES ont été améliorés et adaptés (ce billet en donne une idée brève mais concrète), les étudiants qui intègrent la formation en Master 1 – MEEF ont d’énormes lacunes héritées antérieurement.

Il est aussi déroutant de voir que les programmes de maths changent souvent, et de manière pas toujours cohérente. Petite histoire.

Les étudiants du M2 – MEEF suivent la formation en alternance : ils ont un demi-service d’enseignement dans un établissement secondaire et terminent le Master à l’université. Depuis quelques années j’y assure un cours de Didactique des mathématiques. Je le dispense sous deux formes. La première en traitant un exemple qu’on dévisse, qu’on découpe en plusieurs étapes, on fait le tour de tous ses recoins… La deuxième (la plus fréquente) en faisant exposer chacun des étudiants une de ses leçons ; ce qui amène à un débat pendant lequel nous (ses camarades et moi) apportons des commentaires, des remarques, faisons des suggestions… Une façon de procéder qui s’avère enrichissante et bénéfique, pour nous et plus particulièrement pour l’orateur. Dans le cadre de cette activité, une étudiante nous a exposé sa leçon sur les triangles semblables en classe de Quatrième.

À un moment donné elle a voulu nous montrer comment deux triangles (que nous noterons \(ABC\) et \(A’B’C’\) comme dans le dessin ci-dessous) semblables — mais non isométriques pour ne pas rester dans un cas évident — ont la même forme, plus précisément que l’un est l’agrandissement de l’autre comme pour une photo d’identité et le portrait qu’on en tire.

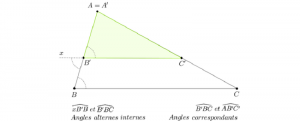
Elle superpose l’angle \(\widehat {A’}\) du plus petit (des deux triangles) sur son homologue \(\widehat A\) du plus grand dans le but de nous faire voir que les côtés opposés \(BC\) et \(B’C’\) sont parallèles. À cet effet, elle rallonge le côté \(B’C’\) et utilise l’égalité des angles alternes internes comme critère de parallélisme. Quelqu’un dans l’assistance lui fait remarquer qu’elle n’avait pas besoin de cette « rallonge », elle pourrait utiliser à cet effet les angles correspondants qu’elle avait déjà à sa disposition. Dans la salle, la réaction a été immédiate : « Ils ne figurent pas au programme de Quatrième ». J’ai vérifié sur le document officiel et j’ai vu qu’on parle effectivement d’angles alternes internes mais pas d’angles correspondants (ni d’angles alternes externes non plus). Naïvement j’ai demandé pourquoi cette omission et quels en sont les auteurs. « Ceux qui n’ont jamais été devant des élèves » m’ont-ils répondu. Eh oui ! quand ça n’est pas clair, ils sont dans la confusion et ont l’impression qu’on ne fait pas ce qu’il faut pour leur faciliter la tâche : ils n’osent pas prendre de risque, ils préfèrent s’en tenir à ce qui est « autorisé ». C’est aussi ce « manque de confiance en soi et de prise d’initiative » dont il faut que nos jeunes enseignants du primaire et du secondaire se débarrassent!

À bon entendeur ! Qui n’entendra peut-être jamais ? Alors tant pis !