Les ficelles du Pilchart

Enfant j’avais été impressionné par cette boîte de conserve qui différait des boîtes cylindriques habituelles.

C’est une boîte de pilchards. ² On disait pilchards alors qu’elle contenait des maquereaux. Ce qui est plus rare maintenant. Toutefois, cela existe encore puisqu’on m’en a trouvé une que l’on m’a offerte. Le pilchard est une sorte de sardine.

Bien plus tard, je me mis à étudier la forme de cette boîte. Il s’avère, avec une bonne précision, que son contour est celui d’une ellipse. Pour qui est sensible aux ellipses cela donne vraiment un attrait et un goût supplémentaire à ce modeste mets. Cette simple boîte sera l’objet de départ pour de nombreuses aventures autour des coniques homofocales.

A l’occasion de la Fête des Lumières à Lyon en 2002, dans le cadre de Superflux, je traçais dans mon atelier la famille ci-dessus d’ellipses et hyperboles homofocales. Elles ont été tracées au moyen d’une ficelle.

Pour les ellipses c’est assez simple, il suffit de tendre une ficelle de longueur supérieure à la distance entre les deux points qui seront les foyers et de déplacer le crayon. En variant la longueur de cette ficelle on obtient une famille d’ellipses de mêmes foyers. Pour les hyperboles c’est un peu plus délicat. Elles ont des branches infinies et par conséquent on ne peut réussir qu’à en tracer des segments.

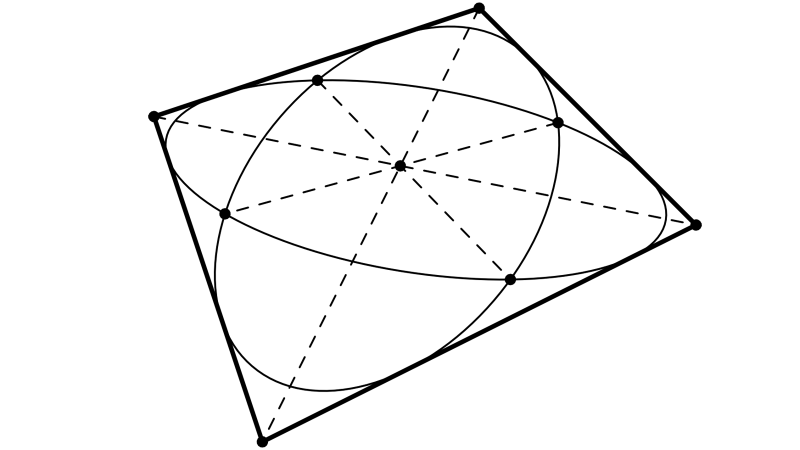
Selon cette procédure, ce qui caractérise une ellipse est la propriété suivante : si je nomme F et F’ les foyers, M le point courant sur l’ellipse et l la longueur de la ficelle (supérieure à la distance FF’), alors MF + MF’ = l. Pour une hyperbole, sous les mêmes conditions, ce sera MF – MF’ = l . Le problème de la différence nécessite d’utiliser une règle rigide qui pivote autour de l’un des foyers. Cette règle rigide ne peut avoir qu’une longueur L finie. Ce qui explique pourquoi on n’obtient que des segments d’hyperbole. A l’extrémité de la règle qui ne pivote pas autour du foyer, on fixe un bout de la ficelle de longueur d. L’autre bout de la ficelle est attaché au deuxième foyer. En appliquant la ficelle contre la règle au point M (la ficelle étant mise en tension ) vous vérifierez que l’on a bien MF – MF’ = L – d. Il suffit de choisir L et d tels que L – d = l . Au besoin vous pouvez vous appuyer sur l’image de la boîte de pilchart où les droites et foyers sont indiqués. Plus L sera grand, plus longs seront les segments des hyperboles.

Pour cette première occasion, puisque c’était la Fête des Lumières, je plaçais, au croisement des ellipses et hyperboles, une LED soudée sur une pile.

Une ambiance lumineuse douce, blanc-bleutée, emplissait mon atelier. En passant, je ferai remarquer que ces ellipses et hyperboles se croisent à angle droit… ce qui n’est pas sans intérêt et pourrait nous renvoyer vers la notion de lignes de champ de forces et des équipotentielles de ce champ. Quel serait le champ de forces qui correspond au pilchart ? J’ai une interprétation… mais je la laisserai de côté pour l’instant.

La deuxième occasion fut celle d’une exposition personnelle au lycée professionnel Sembat-Seguin à Vénissieux (69) en 2003. Au carrefour de deux allées, je traçais ces courbes et plaçais aux intersections une boîte de conserve.

En plein passage, au sortir des ateliers on aurait pu imaginer que la pièce se trouvât rapidement et totalement désorganisée et que les boîtes fussent remises n’importe comment. Ce ne fut pas le cas. Bien évidemment certaines furent déplacées, … (on ne fait pas toujours attention où on met les pieds et dans ce couloir plusieurs centaines d’élèves s’engouffraient) mais elles étaient remises à leur bonne place et, pendant les trois semaines que dura l’exposition, la pièce garda sa fière allure.

Comme suite à cette aventure, la pièce fut achetée par le lycée et pérennisée. Je taillais le sol en béton à la disqueuse et incrustais de la résine.

Par la suite, aux croisements, les élèves réalisèrent des calottes sphériques qui furent fixées en lieu et place des boîtes. Depuis neuf années maintenant, les passants piétinent une figure géométrique et celle-ci ne bronche pas. J’imagine qu’elle en est même plutôt ravie.

Le soir, lorsque le couloir est éclairé, nous avons l’image ci-dessous.

La ligne médiane de ce couloir est marquée par des spots encastrés dans le sol qui font partie de l’architecture et ne relèvent pas de ma décision. Toutefois, avec l’éclairage au plafond qui éclaire la « sculpture », ces points lumineux la prolongent sur toute la longueur de ce couloir de bien 100 mètres.

Reprenons notre boîte de pilchart.

A l’occasion d’un stage où j’évoquai ces ellipses, je dis MF + MF’ = 2r comme je l’avais appris. Un stagiaire me demanda pourquoi 2r. Je fus un peu surpris et lui dis « traditionnellement on dit ainsi, mais appelons la l  ». Quelques instants après je me repris : « si on rapproche F et F’ jusqu’à les confondre, on tracera avec la ficelle un cercle de rayon r = l/2. voilà pourquoi, sans doute on dit traditionnellement 2r ». J’étais surpris car on ne m’avait jamais enseigné à tracer un cercle selon cette méthode et je pense que si on présentait ainsi le cercle conjointement au compas, il serait plus aisé, dès le jeune âge, de tisser des liens. Il serait aussi naturel de tracer une ellipse qu’un cercle. Il suffit d’écarter les points F et F’.

Soit ! Dans le cas concret de la boîte de pilchart, je ne dispose pas à priori des foyers. Si je suppose que cette boîte est bien une ellipse je peux toutefois tracer, sans me soucier de ces foyers, les ellipses extérieures à la boîte et qui lui seront homofocales. C’est un résultat qui a été établi par Graves au 19ème siècle. Prenant une ficelle (une boucle fermée) dont la longueur est supérieure au périmètre de la boîte, entourons la boîte et tendons cette ficelle à l’aide d’un crayon. En déplaçant le crayon nous traçons une ellipse qui est homofocale à l’ellipse définie par la boîte.

Ceci pourrait me faire rebondir vers les billards elliptiques mais je m’abstiendrai. Ceci serait également le point de départ pour cette interprétation de champ de forces et équipotentielles que j’évoquai tout à l’heure.

Je préfère plutôt aborder une expérience qui pourrait être effectuée dès l’école primaire. Je signalais que si les deux foyers sont confondus nous traçons, avec la procédure de la ficelle, un cercle. Prenons maintenant différentes boîtes de conserves cylindriques (à base circulaire… pour être précis puisque la boîte de pilchards est aussi un cylindre) du commerce. Entourons chacune de ces boîtes avec une ficelle. Les longueurs seront différentes. Avant de nouer ajoutons à chacune une même longueur. Nouant, alors, puis traçant avec un crayon, en maintenant la ficelle tendue, nous tracerons un cercle. Ceci n’est qu’un cas particulier de la proposition établie pour les ellipses. Même si cela semble évident ou intuitif dans cette situation circulaire, si vous avez pris soin de tracer le cercle bord de chacune des boîtes, en les ôtant vous observerez les cercles dessinés (concentriques). Puisque le surcroit de fil par rapport au périmètre est constant vous pourrez observer que l’augmentation du rayon n’est pas constante… même si vous ne savez pas la calculer. Cela pourrait être l’occasion, pour des biens plus grands, d’établir la relation entre le surcroit L et le rayon obtenu R en fonction du rayon initial r.

En passant évoquez le cas de la chèvre de Monsieur Seguin attachée à deux piquets distants plutôt qu’un seul, avec un anneau coulissant le long de la corde. Songez, alors, à la force qu’exerce la chèvre sur la corde, etc… une piste pour évoquer les propriétés des tangentes à une ellipse issues d’un même point extérieur à cette ellipse et le champ de forces.

Bien au delà d’une nourriture terrestre, cette modeste boîte de pilchart se révèle une nourriture (poétique ?) pour l’esprit.

Une autre aventure avec les ellipses est ce site Paillart qu’évoquait Etienne Ghys lorsqu’il me présentait dans son article . Un site elliptique dont les « mégalitres » de paille illustraient les douze positions, selon la loi des aires du feu Kepler, d’une planète orbitant autour du foyer tenu par une étoile (ou star ?) ici absente. Ce site de 75 x 62,5 mètres fut également tracé à la ficelle. Cela fera l’objet d’un prochain billet qui s’interroge sur : comment parler d’astronomie et comprendre pourquoi l’héliocentrisme, tel que nous le reconnaissons actuellement, a mis des siècles à s’établir ; avec des bottes de paille ! à des personnes bien peu au fait de ces choses là.