Je voudrais commencer par deux anecdotes personnelles qui m’ont fait prendre conscience de la crainte et du malaise que les mathématiciens ressentent face aux figures et aux images.
Alors que j’étais étudiant de troisième cycle, j’ai eu l’occasion de « surprendre » l’un de mes professeurs en train de faire de petits croquis pour suivre un raisonnement, alors qu’il s’imposait de ne jamais faire la moindre figure au tableau dans son cours magistral. Pourquoi ne partageait-il pas avec ses étudiants cet accès à la compréhension que permettent les figures ?
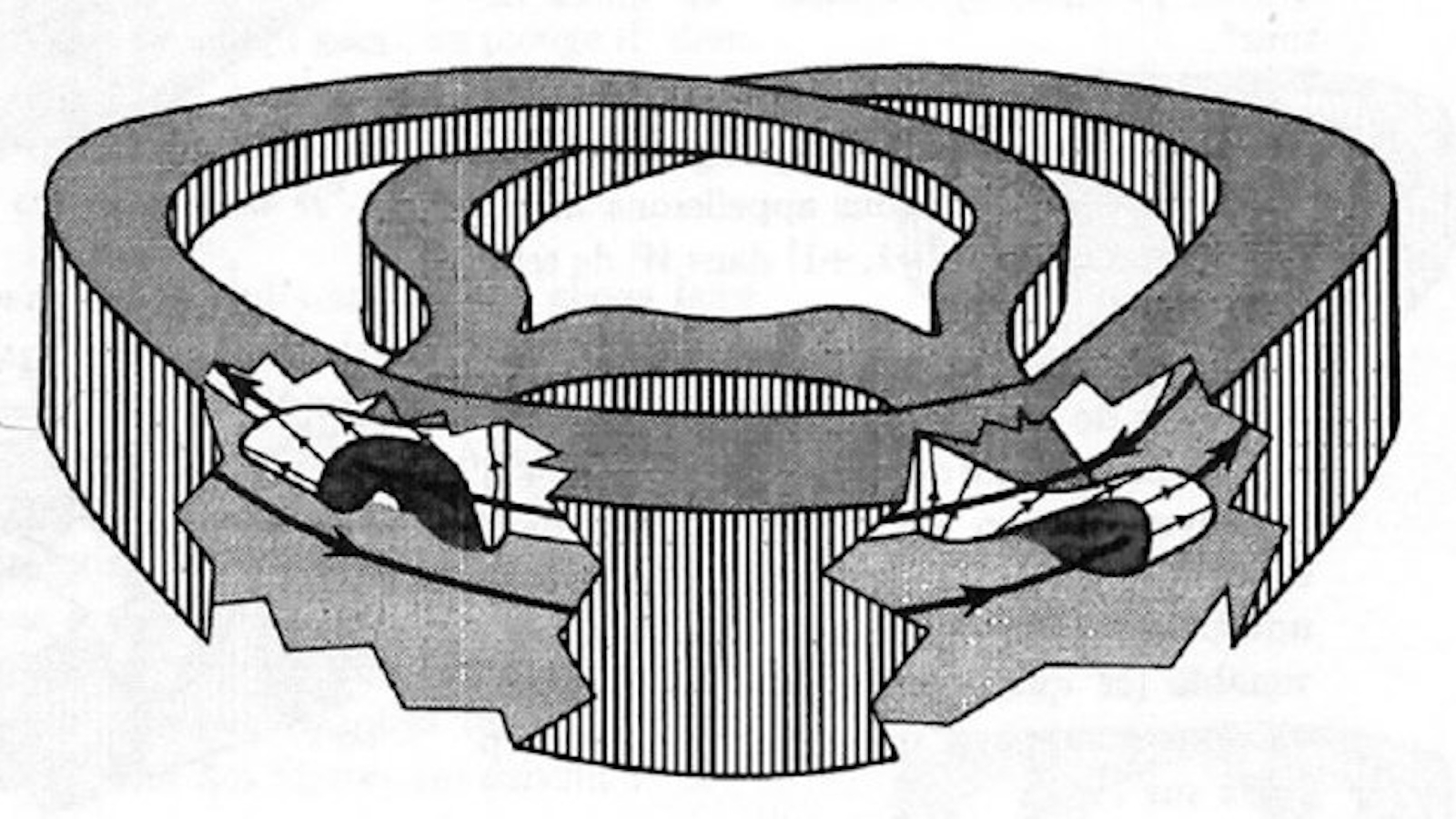
Beaucoup plus tard, à la fin d’une de mes conférences, la réaction d’un éminent collègue m’a beaucoup surpris. J’avais présenté un théorème difficile de topologie où il fallait, comme le veut cette discipline, « couper et coller » de nombreux espaces. Pour faciliter la compréhension de ces constructions, j’avais préparé quelques figures assez élaborées, comme par exemple la figure 1. Ce collègue me demande alors perfidement : « Ce que vous avez expliqué, peut-on dire qu’il s’agit d’un théorème ? » Pourtant, les figures ne permettent-elles pas de démontrer un théorème avec la même rigueur qu’une preuve classique, rédigée avec des mots ?
Figure 1 : Une figure de topologie (à propos d’un théorème de K. Kuperberg).
Clairement, cette « peur de l’image mathématique » est liée au risque d’erreur qu’elle entraîne. Comment se fait-il que les mathématiciens, après tant de siècles de pratique des raisonnements, n’aient pas encore réussi à apprivoiser les images et à les incorporer parmi leurs outils de travail ? Il me semble que ceci est un enjeu pour les mathématiques de demain.
Un peu d’histoire
L’histoire du rapport images/mathématiques mériterait bien sûr une analyse détaillée. On pourra consulter à ce sujet un article très intéressant de Jeanne Peiffer 1J. PEIFFER, Rôle des figures dans la transmission et la production des mathématiques, Images des Mathématiques, CNRS, 2006,. Je voudrais cependant tracer à grands traits (un peu simplistes) les principales périodes de cette histoire.
Chez les grecs anciens, il semble clair que le texte et la figure forment un tout, et qu’on ne peut pas lire l’un sans observer l’autre. Même s’il ne semble pas certain que les éditions originales contenaient des figures, leur description est si précise que le lecteur est invité à les tracer.
Durant la Renaissance, les mathématiciens sont souvent des artistes, des architectes, des ingénieurs. Les figures ont un rôle central, en particulier car les livres écrits par ces auteurs ne sont pas nécessairement lus par des mathématiciens.
C’est au début du XIX° siècle, surtout en France, que commence une période iconoclaste en mathématique. Cela coïncide avec la mise au point des méthodes « rigoureuses » de démonstration et la prise de conscience que les figures peuvent tromper. La citation suivante de Lagrange (en introduction à sa Mécanique Analytique) illustre bien cet état d’esprit.
« Le lecteur ne trouvera pas d’illustrations dans cet ouvrage. Les méthodes que je propose ne nécessitent pas de constructions ou de raisonnement mécanique ou géométrique, mais seulement des opérations algébriques assujetties à une règle de procédure régulière et uniforme. »
Anecdotiquement, il ne faut pas oublier que la gravure des figures coûtait cher et que les éditeurs rechignaient à publier des livres de mathématiques illustrés. Les figures étaient d’ailleurs souvent reléguées en fin d’ouvrage, sur une ou deux pages dépliantes. Bien sûr, il y a des exceptions, comme les livres de géométrie descriptive, dont le but est ouvertement pratique, mais même les traités de Monge consacrés à ce sujet ne sont pas richement illustrés 2G. MONGE, Géométrie descriptive, http://gallica.bnf.fr/.
Ce rejet de la figure en mathématique a continué au XX° siècle, tout au moins en France. Citons Dieudonné, dans les années 1970 :
« C’est ainsi qu’il serait désirable de libérer l’élève dès que possible de la camisole de force des figures traditionnelles, en en parlant le moins possible, au profit de l’idée de transformation géométrique du plan et de l’espace tout entiers… »
En Allemagne par contre, vers la fin du XIX° siècle, une approche plus concrète des mathématiques voit le jour. Les articles de F. Klein sur l’uniformisation de certaines surfaces de Riemann sont illustrés par des figures magnifiques (voir à ce sujet le merveilleux livre 3D. MUMFORD, C. SERIES, D. WRIGHT, Indra’s Pearls : The Vision of Felix Klein, Cambridge University Press, 2002. Voir aussi http://klein.math.okstate.edu/IndrasPearls/). On n’hésite pas à fabriquer toute une série d’objets en plâtre, utilisés dans l’enseignement supérieur, pour représenter un certain nombre de surfaces algébriques (et qu’on retrouve d’ailleurs exposés aujourd’hui dans les salles communes de nombreux départements de mathématiques dans le monde entier). Voir par exemple 4G. FISCHER, Mathematical Models : From the Collections of Universities and Museums. (Deux volumes). Friedr. Vieweg and Sohn, Braunschweig, 1986. et 5A. VIERLING-CLAASSEN, http://www.math.harvard.edu/ angelavc/models/.
Le défi de Hilbert
Au congrès international des mathématiciens de Paris, en 1900, D. Hilbert propose ses fameux 23 problèmes 6Au sujet des problèmes de Hilbert, on peut lire cet article. mais il fait précéder leur description d’un certain nombre de remarques générales sur les mathématiques. En voici un extrait 7D. HILBERT, Mathematische Probleme Vortrag, gehalten auf dem internationalen Mathematiker-Kongreß zu Paris 1900,
http://www.mathematik.uni-bielefeld.de/ kersten/hilbert/rede.html:
« À de nouveaux concepts, il faut associer de nouveaux signes. Nous devons les choisir de telle sorte qu’ils nous rappellent les phénomènes qui ont formé ces concepts. Les figures sont des signes qui nous rappellent l’intuition spatiale, utilisés dans ce but par les mathématiciens. Qui n’utilise pas en simultané avec l’inégalité a<b<c l’image de trois points qui se suivent sur la droite ? Qui n’utilise pas le dessin de segments ou de rectangles emboîtés lorsqu’il s’agit de démontrer rigoureusement la continuité d’une fonction ou l’existence d’un point d’accumulation ? Qui pourrait se passer d’un triangle, d’un cercle et de son centre, ou de trois axes orthogonaux ? Ou qui abandonnerait la représentation d’un champ de vecteurs, ou la figure d’une famille de courbes et de son enveloppe, qui sont si importants dans la théorie des équations différentielles, dans les fondements du calcul des variations ou dans toutes les autres parties des mathématiques ?
Les symboles arithmétiques sont des diagrammes écrits et les figures géométriques sont des formules graphiques. Aucun mathématicien ne pourrait se passer de l’utilisation de ces formules graphiques, pas plus que de l’usage des parenthèses ou d’autres signes dans les formules.
L’utilisation des signes géométriques comme outils de preuves rigoureuses présuppose la connaissance et la maîtrise des axiomes qui sont sous-jacents à ces figures. Pour pouvoir incorporer ces figures géométriques dans le trésor des signes mathématiques, il est nécessaire de commencer par une analyse rigoureuse de leur contenu conceptuel. De la même manière que lorsqu’on ajoute deux nombres, on doit placer les chiffres correctement, l’utilisation et la combinaison des figures géométriques doit être régie par des règles précises. »
Ainsi donc, Hilbert nous met au défi de faire avec les images ce que Viète avait fait avec les symboles algébriques : établir des règles précises pour leur usage, qui leur soient propres et qui permettent de les utiliser comme des outils mathématiques à part entière. Ce défi n’est pas encore relevé mais il devrait l’être dans un futur proche si l’on prend en compte les possibilités extraordinaires proposées par les logiciels de création graphique dont on dispose aujourd’hui. Une image peut maintenant être modifiée, contrôlée ou travaillée avec autant de précision qu’on manipule un fichier texte par exemple.
Quelques tentatives
La théorie des nœuds offre un exemple tout à fait intéressant qui va dans cette direction. Née au cours du XIX° siècle, elle consiste à étudier des diagrammes qui ne sont que de petits croquis tracés dans le plan. Les articles sur ce sujet font figure d’exception dans les revues mathématiques : ils contiennent souvent un grand nombre de diagrammes que l’on manipule de manière presque automatique, un peu comme on manipule des symboles algébriques en suivant des règles bien établies, comme le souhaitait Hilbert. Cette théorie, après s’être quelque peu endormie au cours de la première moitié du XX° siècle, a connu un regain d’activité extraordinaire depuis les années 1980, en particulier — mais pas seulement — à cause de ses liens avec la physique théorique (les diagrammes de Feynman par exemple). Aujourd’hui, on peut manipuler un nœud comme on manipule une inconnue dans une équation. Sur le site internet de D. Bar-Natan par exemple 8D. BAR-NATAN, http://katlas.org/wiki/Main_Page, on trouve toute une série d’outils informatiques qui permettent de travailler avec ces nœuds, de la même manière que les logiciels de calcul formel permettent de travailler avec des équations. Voici une figure extraite de [9]D. BAR-NATAN, Fast Khovanov Homology Computations, Journal of Knot Theory and Its Ramifications, 16-3 (2007) 243-255,9 http://www.math.toronto.edu/ drorbn/papers/FastKh/.
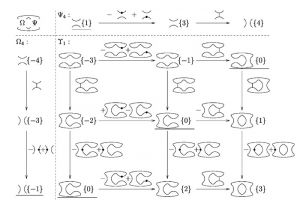
Figure 2 : Extrait d’un article récent de théorie des nœuds.
Voici un autre exemple d’une formule-image extraite d’une thèse récente de probabilités dans laquelle on voit dans la même formule des inégalités, des cosinus, et des diagrammes 10M. HEYDENREICH, A lace-expansion analysis of random spatial models, Ph.D. Eindhoven University of Technology, November 2008, http://www.win.tue.nl/ mheydenr/Heydenreich_proefschrift.pdf.
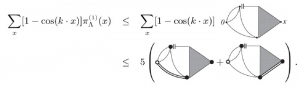
Figure 3 : Extrait d’une thèse de théorie des probabilités.
Mais les diagrammes ne sont que de pauvres images, bien trop élémentaires, et Hilbert avait probablement en tête des images plus riches. Vers la fin du XX° siècle, un certain nombre de mathématiciens ont proposé une renaissance des images dans les mathématiques. Un exemple emblématique est donné par le mathématicien américain W. Thurston qui a renouvelé en profondeur notre façon de comprendre la géométrie des « variétés de dimension 3 ». Il n’est bien sûr pas question d’entrer ici dans le détail de ses travaux et je voudrais me contenter d’un exemple. Sous son impulsion, J. Weeks a été amené à concevoir et réaliser un logiciel appelé SnapPea, qui est un véritable outil visuel de travail pour le topologue en dimension 3 : on y trouve des atlas contenant un grand nombre de variétés, que l’on peut modifier, couper, coller, examiner, faire tourner sur un écran devant ses yeux etc. Cet assistant de travail a eu un impact considérable sur le développement de la topologie de petite dimension (voir 11J. WEEKS, SnaPea, http://www.geometrygames.org/SnapPea/ et 12J. WEEKS, The Shape of Space – How to Visualize Surfaces and Three-Dimensional Manifolds.(1985) Marcel Dekker.). Bien sûr, il ne s’agit encore que d’un outil visuel d’aide à la découverte et le souhait de Hilbert n’est pas encore tout à fait réalisé.
Un théorème de S. Smale de 1957 a surpris plus d’un mathématicien. Il est possible de retourner la sphère sans la déchirer. Cela signifie que si l’on colorie par exemple la face interne d’une sphère en rouge et la face externe en jaune, il est possible de déformer progressivement la sphère en autorisant que certaines parties en pénètrent d’autres, mais sans permettre de déchirure, de sorte qu’à la fin de la déformation, la sphère soit revenue à sa position originale et les deux couleurs aient été échangées. Le simple fait que la phrase précédente soit à peu près incompréhensible pour ceux qui ne sont pas mathématiciens et bien trop imprécise pour ceux qui le sont, montre une fois de plus la difficulté d’exprimer certaines idées mathématiques avec des mots, alors que des images peuvent le faire bien plus facilement. Pour cet exemple, B. Morin et J.-P. Petit ont publié un article dans Pour la Science en 1979, contenant toute une série de dessins qui permettent à la fois de comprendre l’énoncé de ce théorème et sa démonstration 13B. MORIN et J.-P. PETIT, Le retournement de la sphère, Pour la Science 15 (1979), 34-49. Voir aussi http://www.jp-petit.org/science/maths_f/cube_central.htm. Plus impressionnant : W. Thurston et ses collaborateurs ont produit un film autour de ce théorème contenant une preuve qui est tout aussi convaincante — ou peut-être même plus convaincante — que la preuve publiée par Smale 14S. LEVY, D. MAXWELL, T. MUNZNER, W. THURSTON, Outside in, Vidéo distribuée par A.K Peters, disponible sur YouTube http://fr.youtube.com/watch?v=BVVfs4zKrgk. Mieux encore, en une vingtaine de minutes, ce film montre les étapes conceptuelles qui ont conduit à la découverte de ce théorème. Même si l’usage des images dans ce film n’est pas formalisé comme Hilbert l’aurait souhaité, il me semble que ce film contient effectivement la preuve d’un théorème.

Figure 4 : Retourner la sphère.
La figure précédente est extraite de ce film. À gauche on montre quelques étapes du retournement de la sphère (qui passe progressivement du jaune au rouge), et à droite l’une de ces positions intermédiaires, pour le moins alambiquée ! Pour une compréhension complète, nous recommandons au lecteur de visionner le film.
Bien sûr, les images sont loin d’être les seuls concepts utilisés par les mathématiciens et il ne faudrait pas non plus leur donner un rôle exagéré ! Mais les images ont envahi notre société et sont devenues — qu’on le veuille ou non — l’un des principaux moyens de communication d’aujourd’hui. Il faut maintenant que les images prennent la place qu’elles méritent au cœur des mathématiques. Il faut relever le défi de Hilbert :
« Incorporer ces figures géométriques dans le trésor des signes mathématiques ».
Bibliographie
Cette note est la rédaction d’une conférence à l’Académie des Sciences le 6 mai 2008 dans un colloque intitulé « La vertu créatrice du symbolisme mathématique ». Elle reprend un article de la Lettre de l’Académie des Sciences, datée de décembre 2008.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.