
Pierre Berger est chargé de recherches au CNRS. Il travaille au sein du Laboratoire d’Analyse, Géométrie et Applications à l’Université Paris 13. Il a récemment démontré plusieurs théorèmes qui indiquent que l’évolution de certains systèmes est mal modélisée par des statistiques. Nous lui avons demandé de nous expliquer ces résultats.
Bonjour Pierre. Tout d’abord, peux-tu nous dire dans quel domaine des mathématiques tu travailles ?
J’étudie le comportement des systèmes dynamiques chaotiques.
Un système dynamique, c’est simplement un système dont l’état évolue au cours du temps selon une loi déterminée, appelée loi d’évolution. De tels systèmes apparaissent fréquemment en physique, en biologie, en économie…
On donne souvent comme exemple le Système Solaire. L’état du système à un instant donné est l’ensemble des positions et des vitesses des différentes planètes ; la loi d’évolution est celle qui donne l’accélération des planètes en fonction de leur position (grâce à la loi de gravitation de Newton).
Un autre exemple classique est celui d’un écosystème constitué d’un petit nombre d’espèces. L’état du système à un instant donné est le nombre d’individus de chaque espèce. On peut construire des modèles qui fournissent une loi d’évolution. Cette loi traduira des considérations du genre « à un instant donné, la croissance du nombre de moutons est proportionnelle au nombre de moutons, mais inversement proportionnelle au nombre de loups ».
Ce n’est pas parce que l’on sait mettre un système en équations — c’est-à-dire déterminer sa loi d’évolution —, qu’on le comprend bien. La loi d’évolution nous donne l’état du système à l’instant suivant. Le défi est de décrire son comportement sur des durées beaucoup plus longues.
Parfois, le comportement à long terme est très simple et très régulier. Par exemple, un pendule (sans frottement) effectue un mouvement d’oscillation périodique, parfaitement descriptible à long terme (c’est cette régularité qui permet de fabriquer des horloges !). C’est aussi le cas de deux corps isolés dans l’espace soumis à leur seule force d’attraction mutuelle (typiquement une étoile et une planète qui « gravite » autour) : la trajectoire de chacun de ces corps est une ellipse parcourue périodiquement.
La théorie du chaos est née quand Henri Poincaré a découvert que trois corps isolés dans l’espace (typiquement une étoile et deux planètes), soumis à leurs seules attractions mutuelles, peuvent avoir des trajectoires extrêmement complexes. Poincaré a montré que l’on ne peut pas prévoir la position à long terme des planètes pour deux raisons. D’abord, on ne peut pas trouver de formule analytique qui donne la position des planètes en fonction du temps. De plus, si on simule l’évolution du système à partir de plusieurs positions initiales des planètes légèrement différentes les unes des autres, on découvre des mouvements radicalement différents : un infime changement dans les positions initiales modifie complètement les trajectoires à long terme 1H. Poincaré, Sur le problème des trois corps et les équation de la dynamique, Acta mathematica, 13, p. 1- 270 (1890). 2Le résultat de Poincaré concerne un système simplifié, et seulement certaines positions et vitesses initiales très particulières. Cependant, on a montré récemment que ce résultat théorique avait des manifestations dans notre Système Solaire. Grâce à des algorithmes sophistiqués, Jacques Laskar et ses collaborateurs ont pu calculer l’évolution du Système Solaire sur une durée de plusieurs milliards d’années. Dans ces calculs, un changement de moins d’un centimètre dans les positions initiales des planètes change complètement la face du système à long terme : ces infimes variations des positions initiales peuvent entraîner une collision entre Mercure et Vénus, entre Vénus et la Terre, ou entre La Terre et Mars, dans un peu moins de quatre milliards d’années ! J. Laskar. Le Système Solaire est-il stable ? Séminaire Poincaré XIV (2010), page 242
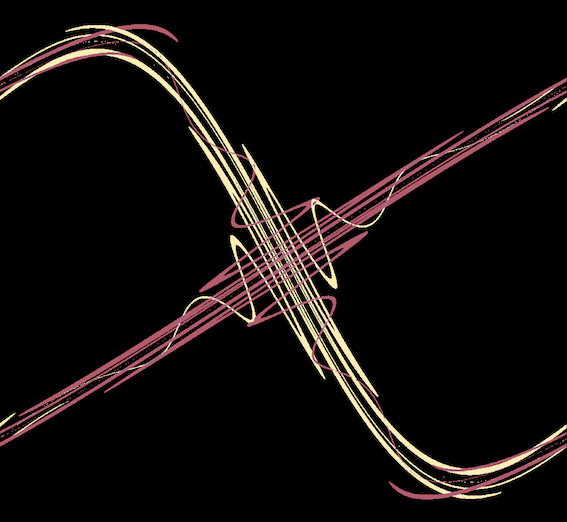
Image d’un treillis homocline. Poincaré a découvert que cette figure géométrique interdit d’écrire l’évolution d’un problème à trois corps sous la forme d’une formule analytique : il faudrait d’abord savoir décrire par des fonctions analytique la figure ci-dessus, ce qui est impossible car les courbes jaunes et rouges ont se replient et s’intersectent de manière trop complexe.
Un système est dit chaotique si une infime perturbation de son état initial peut bouleverser entièrement son évolution.
La théorie du chaos étudie les propriétés de l’évolution de tels systèmes. Bien sûr, comme il s’agit de mathématiques, on oublie la signification des variables décrivant l’état du système, pour ne retenir que les valeurs. Cette abstraction permet de se concentrer sur les mécanismes mathématiques les plus simples engendrant un comportement chaotique.
Les mathématiciens qui travaillent dans ce domaine cherchent à classer les systèmes dynamiques suivant la complexité de leur comportement. Parfois, ils montrent que certaines propriétés restent valides pour une large classe de systèmes. D’autres fois, ils prouvent au contraire que beaucoup de systèmes ne vérifient pas des propriétés pourtant attendues…. 3Plusieurs articles du site parlent du « chaos ». En voici un, élémentaire : Le moulin à eau de Lorenz et deux autres, plus difficiles d’accès : Sculptures du chaos et Hadamard et les systèmes dynamiques.
Tu as récemment démontré des résultats qui affirment que certains dynamiques possèdent une infinité « d’attracteurs statistiques ». Peux-tu expliquer de quoi il s’agit ?
En sciences (humaines, physiques, biologiques, etc.), quand un système montre un comportement complexe, on le modélise par défaut par des probabilités et des statistiques. Cela fonctionne extrêmement bien pour certain systèmes.
Considérons par exemple un système constitué de plusieurs boules en mouvement dans une boîte ayant des collisions sans perte d’énergie. Ce système a un comportement très complexe : les chocs entre les boules ne cessent de faire changer celles-ci de direction. De plus, comme le montre le film ci-dessous, le moindre changement dans la position d’une des boules va modifier radicalement les trajectoires de toutes les autres au bout d’un certain temps : le système est chaotique.
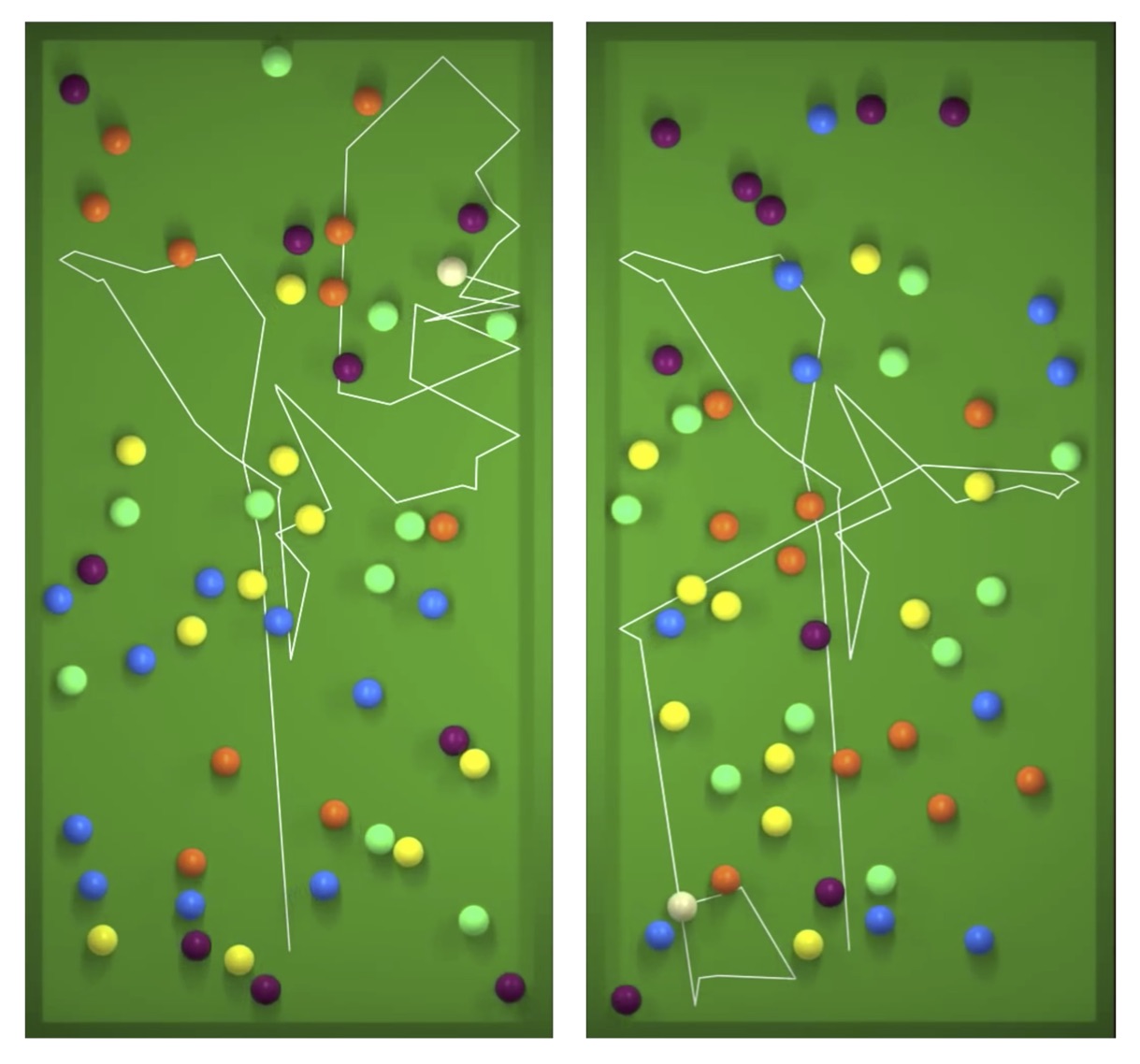
Simulation numérique d’un billard idéal, sans frottement, avec cinquante boules interagissant par chocs parfaitement élastiques. La ligne brisée représente la trajectoire de la boule blanche. Les deux images correspondent à l’évolution du système à partir de deux états initiaux légèrement différents : une seule des cinquante boules a été légèrement déplacée. Plus de simulations sur le site du film Chaos, dont cette image est extraite.
Mais, si l’on s’intéresse à la position des boules d’un point de vue statistique, alors on obtient un résultat très simple. En moyenne dans le temps, chaque boule va visiter avec la même fréquence chaque position et avoir la même fréquence de chocs avec les parois. C’est un théorème assez récent de Yakov Sinai et Nandor Simanyi4 N. Simányi, The K-property of N billiard balls I., Invent. Math. 108, p. 521–548 (1992).

Tirage du loto
Ce comportement — chaotique, mais néanmoins très simple d’un point de vue statistique — est utilisé dans les tirages du loto : les mouvements des boules dans les machines à tirages sont très complexes, on ne peut pas prédire quelle boule va sortir, mais on sait que chaque boule a la même probabilité de sortir que les autres. On peut également vérifier expérimentalement le théorème de Sinai et Simanyi en plaçant un baromètre dans une salle : la pression mesurée (c’est-à-dire le nombre de chocs de molécules d’air sur la membrane du baromètre par unité de temps) ne varie pas d’une seconde à l’autre, et ne dépend pas de la position ou de l’orientation du baromètre dans la pièce.
Dire qu’un système admet un nombre fini d’attracteurs statistiques signifie en gros que le comportement statistique de ce système est bien décrit par un nombre fini de lois de probabilités. Le comportement d’un tel système peut être chaotique, mais on arrive à le comprendre quand on l’étudie d’un point de vue statistique.
Jusqu’à récemment, beaucoup de mathématiciens étaient optimistes en pensant qu’un système dynamique typique ne possédait qu’un nombre fini d’attracteurs statistiques. On savait pourtant depuis les résultats de Sheldon Newhouse 5S.E. Newhouse, Diffeomorphisms with infinitely many sinks, Topology, 13, p. 9-18 (1974).que, pour certains systèmes dynamiques, il existe des perturbations du système ayant une infinité d’attracteurs avec des comportements statistiques différents. Cependant, on conjecturait que ces perturbations étaient improbables, non typiques.

Sheldon Newhouse
Tu parles de système dynamique « typiques ». C’est quoi ? Pourquoi s’intéresser à des systèmes typiques ?
D’une part, cela limite la possibilité d’avoir des phénomènes pathologiques. Par exemple, si on prend un système qui n’évolue pas (la loi d’évolution consiste à « rester tel quel »), alors chaque état initial du système donne lieu à un comportement différent (qui consiste à rester dans cet état). Il y a donc autant d’attracteurs statistiques que d’état initiaux possibles. Pourtant, le système a un comportement très simple et n’est pas du tout chaotique… On veut écarter ce genre de comportements « dégénérés », pour se concentrer vers des comportements plus « typiques ».
D’autre part, si l’on part avec des motivations physiques, il ne faut pas oublier que toute modélisation passe par des approximations. Par exemple, quand on met en équations le mouvement d’un pendule, on néglige généralement le fait que la tige qui supporte le pendule n’est pas parfaitement rigide, que l’air exerce un frottement sur le pendule, etc. Autrement dit, la loi d’évolution du vrai système physique est une petite perturbation de la loi d’évolution du modèle. C’est pour cette raison que, lorsqu’on étudie le comportement d’un système dynamique, on aimerait idéalement trouver des propriétés qui sont satisfaites par « la plupart » des petites perturbations de ce système.
Plus généralement, à défaut d’avoir des propriétés valables pour tous les systèmes dynamiques (ou tous les systèmes d’un certain type), on cherche des propriétés valables pour des systèmes dynamiques « typiques », c’est-à-dire pour « la plupart » des systèmes dynamiques.
Cela explique pourquoi on s’intéresse aux systèmes typiques. Mais comment détermine-t-on si un système est « typique » ou pas ? Autrement dit, comment définit-on un système dynamique typique ?
C’est un peu délicat. Tout d’abord, parler de systèmes dynamiques typiques est un raccourci. On devrait parler de « propriété typique » pour les systèmes dynamiques : une propriété est dite « typique » si elle est vérifiée pour la plupart des systèmes.
- Reste à définir ce qu’on entend par « la plupart des systèmes dynamiques ». La première idée qui vient à l’esprit est de tirer des systèmes dynamiques au hasard, et de dire qu’une propriété est typique si la probabilité de tirer un système vérifiant cette propriété est égale à 1. Hélas, on n’arrive pas à formaliser cette idée. Le problème est que, pour tirer au hasard, il faut définir une mesure de probabilité. Par exemple, quand on dit que l’on tire un nombre entier au hasard entre 1 et 1000, on suppose que tous les nombres ont la même probabilité d’être tirés, ce qui revient à dire que l’on considère la mesure de probabilité sur l’ensemble 1,…,1000 qui donne un poids de 1/1000 à chaque élément de cet ensemble. Mais il s’avère qu’il n’existe pas de mesure de probabilité « naturelle » sur l’ensemble de tous les systèmes dynamiques. C’est lié au fait que l’ensemble de tous les systèmes dynamiques est de dimension infinie.
Il y a eu différentes propositions pour contourner ce problème. L’une d’elles est due à A. Kolmogorov 6 Voir l’article (en Russe) de A. Kolmogorov dans les Proceedings of the International Congress of Mathematicians 1954. Cet article est traduit en anglais dans le livre de Foundations of mechanics de R. Abraham et J. E.Marsden (Addison-Wesley Publishing Company).. Elle consiste à considérer des perturbations d’un système dynamique qui dépendent d’un paramètre, puis à tirer la valeur du paramètre au hasard. Cette fois-ci c’est possible parce que le paramètre est un nombre, et il y a une probabilité très naturelle sur l’ensemble des nombres.

Andrey Kolmogorov
Une propriété est typique si quand on tire la valeur du paramètre au hasard, on obtient un système qui vérifie cette propriété avec une probabilité égale à 1. C’est pour cette notion de typicité « au sens de Kolmogorov » que j’ai obtenu des résultats.
Qu’as-tu démontré pour pour ces systèmes « typiques » ?
En gros, j’ai montré l’existence de systèmes dynamiques typiques au sens de Kolmogorov qui admettent une infinité d’attracteurs statistiques. Le comportement d’un tel système est très mal modélisé par les statistiques : de petites variations de l’état initial du système conduiront à des évolutions complètement différentes, même d’un point de vue statistique 7P. Berger, Generic family with robustly infinitely many sinks, Inventiones Mathematicae, 205, 121 (2016). 8P. Berger, Emergence and non-typicality of the finiteness of the attractors in many topologies, arXiv:1609.08803,09/2016..
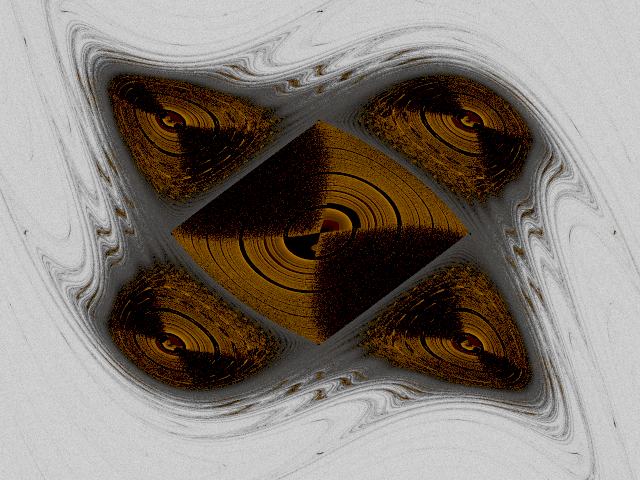
Un système dynamique (connu sous le nom de standard map) qui possède vraisemblablement une infinité d’attracteurs statistiques.
L’image représente l’ensemble des états possibles du système. Chaque point de l’image doit être vu comme un état initial possible du système. Les différentes « taches dorées » correspondent à différents ensembles d’états initiaux qui, potentiellement, donneront lieu à des comportement statistiques différents du système.
Concrêtement, que signifie ton résultat ?
Ce résultat nous laisse face à une alternative : soit la notion de typicité au sens de Kolmogorov n’est pas pertinente pour l’étude des systèmes dynamiques (autrement dit, les systèmes physiques réels ne sont pas typiques au sens de Kolmogorov), soit — et c’est mon opinion — il y a réellement beaucoup de systèmes physiques dont le comportement est difficile, voire impossible, à décrire par des statistiques.

Zoom sur une partie de l’image précédente
Post-scriptum
François Béguin et Pierre Berger remercient les relecteurs dont les noms ou pseudonymes sont janpol3, Marielle Simon, Valkil07, alchymic666, Damien Gayet et Michaël Bages pour leur relecture attentive et leurs commentaires. Ils remercient également Fabio Seixo qui nous autorise à reproduire la photo utilisée en tête de l’article.




11h04
J’ai été fasciné par cet article : merci !
Les travaux de monsieur Berger pourraient-ils conduire à devoir préciser mieux le domaine d’application de l’hypothèse ergodique, ou, carrément, conduire à la remettre en cause ?
WIKIPEDIA : L’hypothèse ergodique, ou hypothèse d’ergodicité, est une hypothèse fondamentale de la physique statistique. Elle fut formulée initialement par Ludwig Boltzmann en 1871 pour les besoins de sa théorie cinétique des gaz. Elle s’appliquait alors aux systèmes composés d’un très grand nombre de particules, et affirmait qu’à l’équilibre, la valeur moyenne d’une grandeur calculée de manière statistique est égale à la moyenne d’un très grand nombre de mesures prises dans le temps. La première valeur est celle que permet de calculer la physique statistique, la seconde est proche de ce qu’on peut expérimentalement mesurer. L’hypothèse ergodique est donc fondamentale pour un bon rapprochement entre la théorie et l’expérience.
11h10
Même question pour la méthode de Monte-Carlo puisqu’ après tout, il s’agit de résoudre des équations aux dérivées partielles (qui peuvent « être chaotiques ») avec des méthodes statistiques (qui peuvent « être chaotiques »)
D’ailleurs, pourrait-on imaginer que la résolution « analytique » ou « probabiliste » donnent des chaos différents ?
Cet article m’a réellement fait rêver 😉 !
WIKIPEDIA : Le véritable développement des méthodes de Monte-Carlo s’est effectué sous l’impulsion de John von Neumann et Stanislaw Ulam notamment, lors de la Seconde Guerre mondiale et des recherches sur la fabrication de la bombe atomique. Notamment, ils ont utilisé ces méthodes probabilistes pour résoudre des équations aux dérivées partielles dans le cadre de la Monte-Carlo N-Particle transport (MCNP).
21h07
Bonjour et merci pour cette intéressante interview.
Je voudrais par contre exprimer mon désaccord concernant la phrase « On peut également vérifier expérimentalement le théorème de Sinai et Simanyi en plaçant un baromètre dans une salle […] ».
Un théorème se démontre, il ne se vérifie pas expérimentalement. C’est, à mon avis, le contraire de la phrase citée qui est le cas : c’est le comportement du baromètre qui s’expliquera par le théorème, si des mesures physiques permettent de vérifier que l’on est bien dans les conditions d’application dudit théorème (je n’ai pas consulté les hypothèses ni effectué de mesures, donc je ne sais pas si c’est le cas).
Cordialement,
TS