L’inégalité isopérimétrique est la solution d’un problème simple à expliquer, pas évident à résoudre, et qui offre une multitude de variantes et de développements.
Dans le plan
Le problème qui nous intéresse est le suivant : si on dispose d’une corde de longueur fixée, disons \(\ell\), quelle est la plus grande surface qu’on puisse entourer avec cette corde ?
On peut par exemple disposer la corde le long d’un carré de côté \(\ell/4\), et on obtiendra une surface \(\ell^2/16\). Mais il paraît plus malin de disposer
la corde le long d’un cercle. En effet, si on se rappelle que le périmètre d’un cercle est \(2\pi\) fois son rayon, on voit qu’on peut entourer un disque de
rayon \(\ell/(2\pi)\). Mais alors la surface de ce disque est \(\pi\) fois le carré de son rayon, soit \(\ell^2/(4\pi)\). On sait bien que \(\pi\) est plus petit
que \(4\), donc \(\ell^2/(4\pi)\) est bien plus grand que \(\ell^2/16\).
.
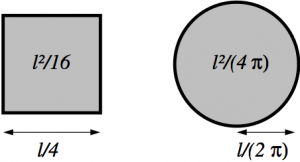
L’inégalité isopérimétrique dit précisément que, quelle que soit la forme que l’on entoure avec la corde, la surface entourée \(S\) vérifie toujours
\[4\pi S\leq \ell^2.\]
Autrement dit, on ne peut pas trouver une meilleure forme que le cercle pour entourer beaucoup de surface : on dit que le cercle est isopérimétrique. Mieux, on sait aussi démontrer que seul le cercle permet d’obtenir la plus grande surface possible.
Il est remarquable qu’une des démonstrations les plus connues de ce théorème utilise les séries de Fourier, que Joseph Fourier introduisit pour étudier un problème complètement différent, à savoir la diffusion de la chaleur. Mais sa théorie s’est révélée tellement féconde qu’il faudrait des centaines de billets pour en décrire toutes les applications.
Dans l’espace
On peut se poser un problème analogue dans l’espace : si on considère tous les objets de surface \(s\), quel est la valeur maximale de leur volume \(V\) et quand est-elle atteinte ?
On peut montrer (mais pas en utilisant les série de Fourier, malheureusement) qu’encore une fois c’est la sphère qui réalise le plus grand volume. L’inégalité isopérimétrique
dans l’espace s’écrit
\[36\pi V^2\leq s^3\]
et l’égalité est réalisée par les sphères, et seulement elles.
.
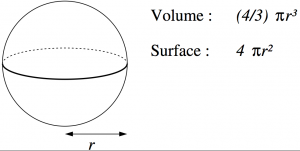
Au-delà
On peut généraliser ce problème à des dimensions supérieures à 3, même si les non mathématiciens trouvent souvent cette idée étrange, mais je n’en dirai rien sinon qu’on obtient une réponse du même genre qu’en dimension 2 et 3.
Un aspect remarquable de ce problème est la quantité pléthorique de variantes intéressantes qu’il a généré. La plus connue est le problème de Didon. L’histoire raconte qu’en débarquant sur la côte africaine, Didon reçu le droit de s’approprier la partie de terrain de bord de mer qu’elle réussirait à entourer avec une peau de bœuf. Son idée fut de découper la peau en fines lanières de façon à obtenir une corde assez longue. Il lui restait à déterminer quelle forme donner à la corde pour entourer un maximum de terrain, qui deviendrait Carthage. Il faut noter qu’elle pouvait aussi se servir de la côte supposée droite 4La légende a été un peu arrangée ici par les matheux pour les besoins de la cause. aussi bien que de sa peau de bœuf comme frontière. Je vous laisse chercher quelle forme est optimale, en indiquant seulement qu’elle se déduit de l’inégalité isopérimétrique.
La recherche contemporaine en géométrie fait une large place à l’étude de l’inégalité isopérimétrique dans des espaces « courbés », mais même la version que j’ai exposée est étudiée et raffinée de nos jours. C’est là-dessus que je voudrais finir.
La question de la stabilité
Reprenons nos problèmes en dimension deux et trois ci-dessus. On sait quelles sont les formes optimales (le cercle et la sphère), mais imaginons qu’on dispose d’un objet qui soit presque optimal, c’est à dire que l’inégalité isopérimétrique est très près d’être une égalité pour cet objet. Cet objet est-il forcément presque rond ? Ce type de problème est une question de stabilité (on se demande si la forme du domaine est stable à proximité de l’égalité).
La réponse est positive en dimension 2 et R. R. Hall 5J. Reine Angew. Math. 428 (1992), 161—176 a démontré une version quantitative très précise : son résultat mesure le « défaut de rotondité » maximal en fonction du « défaut d’isopérimétrie » du domaine.
En dimension 3, le résultat est faux pour la notion la plus immédiate de défaut de rotondité. En effet, si on prend comme domaine une sphère à laquelle on ajoute un « nez » très long et très très fin, on obtient une surface et un volume très proche de ceux d’une sphère, donc le défaut d’isopérimétrie est très petit alors qu’on a spontanément envie de dire que le domaine est très loin d’être rond.
.
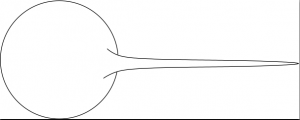
Toutefois, il y a stabilité pour une notion de « défaut de rotondité » bien précise. On peut en effet montrer que si un domaine est presque isopérimétrique, alors il y a une sphère qui délimite presque le même espace que le domaine : le volume à l’intérieur du domaine mais extérieur à la sphère, et le volume intérieur à la sphère mais extérieur au domaine sont tous les deux très petits. On dit que l’assymétrie de Fraenkel est très petite. Hall avait aussi démontré ce résultat, mais avec une estimation de l’assymétrie de Fraenkel peut satisfaisante.
La version optimale de ce résultat a été démontrée récemment par trois mathématiciens italiens, N. Fusco, F. Maggi et A. Pratelli et publiée dans la prestigieuse revue Annals of mathematics 6Ann. of Math. (2) 168 (2008), no. 3, 941—980.. Je trouve remarquable qu’un problème si ancien soit toujours aussi intéressant. D’ailleurs l’histoire n’est pas finie : par exemple on ne sait pas quels sont les domaines « les moins ronds » qui ont un défaut d’isopérimétrie fixé.
ÉCRIT PAR
Benoît Kloeckner
Chercheur associé - Laboratoire d’Analyse et de Mathématiques Appliquées - Université Paris-Est Créteil Val de Marne
