L’interpolation linéaire, une méthode de calcul que beaucoup utilisent, souvent de façon implicite et probablement sans comprendre ce qu’il y a derrière.
J’en ai découvert le principe en Terminale, juste après la leçon sur la fonction logarithme
\(\ell n:{\Bbb R}_+^\ast \longrightarrow {\Bbb R}\) qu’on nous a définie par \(\ell n(x)=\int_1^x{{dt}\over t}\) au seul motif que la formule classique Primitive de \(x^n={{x^{n+1}}\over {n+1}}\) n’est valide que si \(n\neq -1\).
La propriété fondamentale de cette fonction \(\ell n(xy)=\ell n(x)+\ell n(y)\) fut presque une révélation lorsqu’on nous a montré ce qu’on peut en faire, en particulier calculer des valeurs approximatives de certaines quantités « compliquées », telles par exemple :
\[x={{\sqrt{917}(333)^{1\over 3}(425)^{1\over 11}}\over {(777)^{1\over 7}}}.\]
À cette époque, nous savions extraire (à la main) la racine carrée d’un entier naturel mais pas la racine cubique et encore moins la racine septième, onzième…
Nous n’imaginions pas l’existence de la calculatrice, nous étions loin de penser qu’une machine pouvait se substituer à une tête humaine pour une telle tâche. (Moi, personnellement, je ne me doutais même pas de celle de la règle à calcul !)
La fonction logarithme était notre seul recours : calculer \(\ell n(x)\), en usant de la relation fondamentale susmentionnée et chercher sur la table de logarithmes la valeur approchée qui lui correspond. Mais on ne tombait pas toujours dessus. Il fallait y repérer deux valeurs encadrant la nôtre et procéder à une interpolation linéaire. C’était donc l’occasion d’user de cette méthode de calcul approché.
Nous avions appris (auparavant en classe de première) qu’en zoomant sur un morceau du graphe d’une fonction dérivable, on peut le voir comme un segment de droite. C’est ce qui se passe par exemple sur le dessin du logo représentant le graphe du logarithme népérien : sur l’intervalle \([11,14]\), il est presque un segment, ce qui signifie que la fonction \(\ell n\) peut y être pratiquement considérée comme une fonction linéaire. Ceci facilite par exemple le calcul
approximatif de la valeur de \(x\) dont le logarithme \(2,46\) (en supposant qu’on ne le voit pas sur la table) est encadré par \(\ell n(11)=2,39\) et \(\ell n(14)=2,64\).
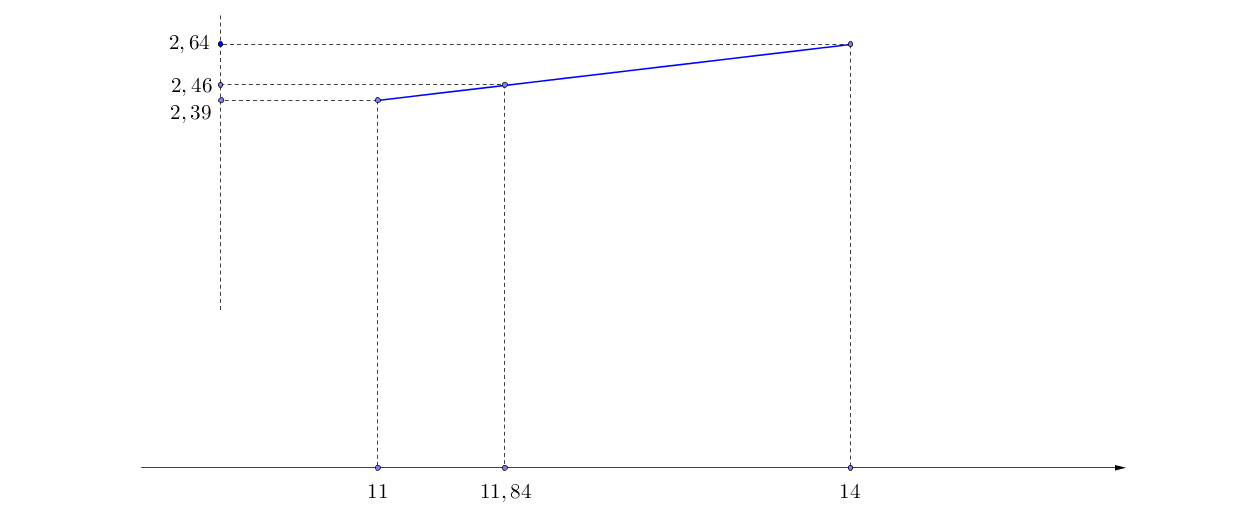
Comme la fonction \(\ell n\) est supposée linéaire sur l’intervalle \([11,14]\), on a \({{x-11}\over {14-11}}={{\ell n(x)-\ell n(11)}\over {\ell n(14)-\ell n(11)}}\). En remplaçant par les valeurs numériques que nous avons, on trouve \(x\simeq 11,84\). Le calcul direct de \(\ell n(11,84)\) donne \(2,47\) qui n’est pas loin de \(2,46\).
Beaucoup diront que tout cela est maintenant obsolète : il y a des calculatrices perfectionnées, des ordinateurs puissants… pour faire tous ces calculs et d’autres encore plus compliqués. C’est vrai, et j’en conviens si c’est juste pour quelqu’un qui n’a besoin que du résultat numérique pour une raison ou une autre (un banquier, un industriel… ) et qui se fout systématiquement des maths. Mais peut-on tolérer que beaucoup d’étudiants en Master de Mathématiques ne sachent pas faire cela ? (Et surtout s’ils se destinent à la fonction d’enseignant.) Cette méthode d’interpolation mélange des idées très utiles, présentes dans pléthore de mathématiques et, surtout, simples à comprendre :
— ce qu’il y a derrière la dérivabilité ;
— la notion de proportionnalité, capitale ;
— des calculs pratiques qu’on rencontre dans la vie réelle ;
— ⋯
Alors pourquoi continuer à abandonner ce genre de choses sous prétexte qu’il y a des machines qui peuvent faire le job ? C’est drôlement curieux qu’actuellement, dans l’enseignement des mathématiques, on ait toujours recours aux facilités au détriment de toutes les notions de base, qui demandent de l’effort certes, mais qui sont le socle et la solidité du savoir dans cette discipline !
ÉCRIT PAR
Aziz El Kacimi
Professeur émérite - Université Polytechnique Hauts-de-France
