
Défi de la semaine
Charlie fait la somme de tous les entiers entre deux entiers \(a\) et \(b\), en comptant \(a\) et \(b\). Si \(1\leq a\leq 10\) et \(11\leq b\leq 20\), alors parmi les nombres \(91\), \(92\), \(95\), \(98\) et \(99\), lequel n’est pas une somme possible pour Charlie ?


Solution du 3e défi de mars 2024
Il y a \(24\) cases, donc on va devoir utiliser huit formes. La somme de tous les nombres est égale à \(120\), donc la somme dans chaque forme doit être égale à \(15\). En raisonnant par exemple à partir des cases 8 du coin en haut à droite, on peut vérifier que la seule manière de couvrir le carré est la suivante :
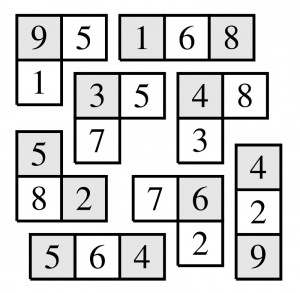
.
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock





15h10
La somme en question est la différence entre la somme des b premiers entiers et celle des a-1 premiers entiers.
C’est donc \(b(b+1)/2 – (a-1)a/2 = (1/2)(b^2-a^2+b+a) = (1/2)(b+a)(b-a+1)\)
Bien sûr, il est possible d’opérer les 10*10=100 calculs différents et observer celle des sommes proposées qui ne sort pas.
Mais, puisque dans la formule dernière apparaissent deux facteurs qui sont de parités différentes, la somme n’est paire que si b+a = 0 mod 4 ou si b-a+1 = 0 mod 4.
Risquons-nous à essayer de constater que c’est l’une des solutions paires qui n’est pas possible ; nous avons 3 chances sur 5 de perdre notre temps, et 2 sur 5 d’en gagner.
La première condition est équivalente à a et b pairs, ce qui peut conduire à 25 sommes.
La seconde est équivalente à b-a = 3 mod 4, ce qui peut conduire à 11 sommes (nombre établi ici par déroulement des possibilités).
Par la première condition, et une fois de plus par déroulement des possibilités, nous tombons sur la somme des entiers de 8 à 15 égale à 92.
Nous poursuivons par cette première condition, puis par la seconde, et nous ne tombons pas sur 98.
98 n’est pas une somme possible pour Charlie.
Répondre à ce message |
10h08
\(91=7*13\)
\(92=2*2*23\)
\(95=5*19\)
\(98=2*7*7\)
\(99=3*3*11\)
Une de ces cinq valeurs n’est pas possible. C’est-à-dire que l’une des valeurs ne respecte pas une contrainte.
\(a+…+b=(1+2+…+(a-1)+a+…+b)-(1+2+…+(a-1))\) ou \(a+…+b=(b+1).b/2-(a).(a-1)/2\) ou encore \(a+…+b=(b+a).(b-a+1)/2\)
Quand l’un des facteurs est impair, l’autre est pair. Quand on divise celui des deux qui est pair par \(2\), il peut donner un résultat pair ou impair.
Quand la division donne un résultat impair, le produit est impair, sans que je vois de contrainte particulière donc rien n’empêche \(91\), \(95\) et \(99\) d’être des résultats de la somme \(a+…+b\).
Quand la division donne un résultat pair, le produit est pair avec pour contrainte que le facteur qui était pair devait donc rester pair après une division par \(2\) : le facteur pair devait donc être en plus un multiple de \(4\). Le résultat pair de la \(a+…+b\) doit être multiple de \(4\) : \(98=2*7*7\) ne convient pas.
15h08
On a aussi :
\(a+b\) est compris entre \(11\) et \(30\).
\((b+a).(b-a+1)\) peut être égal à \(182=14*13\), à \(184=8*23\), à \(190=10*19\) et à \(198=18*11\) ou à \(198=9*22\).
Amusons-nous avec le dernier, \(198\).
On peut avoir \((b+a)=18\) et \((b-a+1)=11\) ce qui conduit à \(b=14\) et \(a=4\).
On peut avoir \((b+a)=11\) et \((b-a+1)=18\) ce qui conduit à \(b=14\) et \(a=-3\) ce qui n’est pas possible même si la somme des entiers relatifs entre \(-3\) et \(3\) est nulle.
On peut avoir \((b+a)=22\) et \((b-a+1)=9\) ce qui conduit à \(b=15\) et \(a=7\).
On peut avoir \((b+a)=9\) et \((b-a+1)=22\) ce qui conduit à \(b=15\) et \(a=-6\) ce qui n’est pas possible.
Et alors pour \(196=2*2*7*7\) la seule possibilité respectant la contrainte sur \(a+b\) est \((b+a)=14\) et \((b-a+1)=14\) ce qui conduit à \(2.b=27\) ce qui n’est pas possible puisque \(b\) est un entier.
C’est une autre raison pour laquelle \(98\) ne pourra pas être une somme.
L’avantage de cette méthode est qu’elle construit des valeurs de \(a\) et \(b\).
Et j’aime bien avoir montré que \(4+5+…+14=7+8+…+15=99\) soit qu’il existe plus de un couple \((a;b)\) pour une même valeur de somme.
15h14
Ah zut.
On a aussi \(b+a=28\) et \(b-a+1=7\) ce qui donne \(b=17\) et \(a=11\) qui ne respecte pas la contrainte sur \(a\) mais qui donne bel et bien \(11+12+…+17=98\).
Je ne comprends plus la pertinence de mon argument en termes de multiple de \(4\) des sommes paires…
15h57
C’est le produit \((b-a+1)(b+a)\) qui doit être multiple de \(4\) quand sa moitié, la somme de Charlie, est paire. Mais la somme elle-même peut très bien être paire sans être multiple de \(4\). Par exemple avec \(a=9\) et \(b=11\), on a \(9+10+11 = 30 = 2 \times 15\).
16h30
Tout entier supérieur à \(6\) produit d’un entier pair et d’un entier impair est égal à une somme d’entiers consécutifs ?
9h12
Soit \(N=a+…+b\) la somme de tous les entiers compris entre \(a\) et \(b\), \(a\) et \(b\) compris.
Si \(N=(2q).(2.p+1)=a+…+b=((b+a).(b-a+1)/2\) alors
\(b=2.q+p\)
\(a=2.q-p\)
17h33
Notons \(C(a,b) = a+ … +b\) la somme de Charlie. Alors \(C(a,b) = \frac{(b-a+1)(b+a)}{2}\).
De \(1 \leq a \leq 10\) et \(11 \leq b \leq 20\), on tire \(2 \leq b-a+1 < b+a \leq 30\). Comme \(b-a\) et \(b+a\) sont de même parité, il faut décomposer \(2C(a,b)\) en produit de deux nombres de parités opposées, disons \(i\) impair et \(p\) pair, tous deux compris entre \(2\) et \(30\). Par ailleurs la différence des facteurs \((b-a+1)\) et \((b+a)\) est \(|i-p|=2a-1\), et leur somme est \(i+p = 2b+1\). Il faut commencer par chercher \(i\) car il est aussi diviseur impair de \(C(a,b)\), et on en déduit \(p=\frac{2C(a,b)}{i}\), puis \(a=\frac{|i-p|+1}{2}\) et \(b = \frac{i + p - 1}{2}\). Chaque fois qu’on trouve \(p\), \(a\), \(b\) dans les intervalles requis, on tient une solution. Pour \(91=7 \times 13\) on a \(2\) solutions : avec \(i=7\) on obtient \(p=26\) puis \(91=C(10,16)\) avec \(i=13\) on obtient \(p=14\) puis \(91=C(1,13)\) Pour \(92=2^2 \times 23\) on a \(1\) solution : avec \(i=23\) on obtient \(p=8\) puis \(92=C(8,15)\) Pour \(95=5 \times 19\) on a \(1\) solution : avec \(i=5\) on obtient \(p=38 > 30\), trop grand.
avec \(i=19\) on obtient \(p=10\) puis \(95=C(5,14)\)
Pour \(98=2 \times 7^2\) on n’a aucune solution :
avec \(i=7\) on obtient \(p=28\), puis \(a=11>10\), trop grand.
Pour \(99=3^2 \times 11\) on a \(2\) solutions :
avec \(i=3\) on obtient \(p=66 > 30\), trop grand.
avec \(i=9\) on obtient \(p=22\) puis \(99=C(7,15)\)
avec \(i=11\) on obtient \(p=18\) puis \(99=C(4,14)\)
L’intrus est donc \(98\).
20h28
Le sujet indique qu’il n’y a qu’un intrus, or 98 est le seul divisible par un carré. (soupçon)
On a alors (a+b)(b-a+1) = 4×7².
On sait qu’ils ne sont pas de même parité , que (a+b)>(b-a+1) (différence 2a-1) et qu’aucun n’est divisible par 49 donc on ne peut qu’avoir a+b = 28 et b-a+1 = 7 ce qui a = 11 et b =17 : impossible.
Pour être complète 2a-1 n’est négative que si a = 0 mais alors b(b+1) = 2²X7² or ce nombre n’a pas 2 diviseurs consécutifs (sauf 1 et 2).
13h55
La somme des nombres de \(\,a\,\) à \(\,b\,\) est \(\,S(b, a)= \frac{b(b+1)}{2}-\frac{a(a-1)}{2} \)
On sait que \(\,1\leq a \leq 10\,\) donc \(\,0\leq \frac{a(a-1)}{2}\leq 45\)
Et puisque \(\,91\leq \frac{b(b+1)}{2}-\frac{a(a-1)}{2} \leq 99\,\), on a \(\,91 \leq \frac{b(b+1)}{2}\leq 144\,\) d’où \(\,13\leq b \leq 16\)
Si \(\,b=13\,\) alors \(\,91\leq 91-\frac{a(a-1)}{2} \leq 99\,\) soit \(\,-8 \leq \frac{a(a-1)}{2} \leq 0\,\) et \(\,a=1\,\)
Si \(\,b=14\,\) alors \(\,91\leq 105-\frac{a(a-1)}{2} \leq 99\,\) soit \(\,6 \leq \frac{a(a-1)}{2} \leq 14\,\) et \(\,a=4\,\) ou \(\,5\,\)
Si \(\,b=15\,\) alors \(\,91\leq 120-\frac{a(a-1)}{2} \leq 99\,\) soit \(\,21 \leq \frac{a(a-1)}{2} \leq 29\,\) et \(\,a=7\,\) ou \(\,8\,\)
Si \(\,b=16\,\) alors \(\,91\leq 136-\frac{a(a-1)}{2} \leq 99\,\) soit \(\,37 \leq \frac{a(a-1)}{2} \leq 45\,\) et \(\,a=10\,\)
Les sommes possibles sont alors :
\(\,S(13, 1)=91-0=91\, \hspace{2cm}S(14, 4)=105-6=99\, \hspace{2cm}S(14, 5)=105-10=95\,\)
\( \,S(15, 7)=120-21=99 \hspace{1.5cm} S(15, 8)=120-28=92 \hspace{1.8cm} S(16, 10)=136-45=91\, \)
La somme obtenue par Charlie ne peut donc pas être égale à \(98\).