Maryam Mirzakhani, médaille Fields 2014

Il était temps ! Maryam Mirzakhani est donc la première femme à recevoir la médaille Fields.

Maryam Mirzakhani est née en Iran en 1977. Elle a bénéficié en Iran d’une éducation de grande qualité, en particulier grâce à des écoles spécialement destinées aux élèves doués (et douées !). Dans une interview très intéressante, elle donne quelques indications sur sa formation intellectuelle en Iran. Elle a en particulier participé aux Olympiades Internationales des Mathématiques en 1994 et 1995. Elle commence ensuite des études universitaires à l’université Sharif de technologie de Téhéran où elle obtient une licence en 1999.

Par la suite, Maryam Mirzakhani part à Harvard pour soutenir une thèse en 2004 sous la direction de Curt McMullen (médaillé Fields en 1998). Les honneurs et les prix s’enchaînent alors pour aboutir à un poste de professeur à Stanford en 2008 et la médaille Fields en 2014.

Mirzakhani s’intéresse aux surfaces de Riemann, qui sont parmi les objets les plus fondamentaux des mathématiques. A vrai dire, en n’exagérant que très peu, on pourrait dire que les quatre médaillé(e)s Fields 2014 sont intéressé(e)s par les surfaces de Riemann.

Voici une traduction de la citation officielle pour cette médaille.

« Maryam Mirzakhani reçoit la médaille Fields pour ses contributions exceptionnelles à la dynamique et la géométrie des surfaces de Riemann et de leurs espaces de modules ». [1]

Les surfaces de Riemann

Rappelons que les coordonnées cartésiennes permettent d’associer un point du plan à deux nombres et réciproquement.
Dans un premier temps, les nombres utilisés étaient tout naturellement des nombres réels.
Si on part d’une équation polynomiale de la forme \(P(x,y)=0\), on peut lui associer une « courbe algébrique » : c’est l’ensemble des points dont les coordonnées satisfont cette équation.
\(y-2x=1\) représente une droite et \(x^2+y^2=1\) un cercle.
Mais les nombres réels peuvent parfois nous jouer des tours.
Par exemple la courbe \(x^2+y^2+1=0\) ne contient aucun point… réel.
En revanche, si on passe aux {nombres complexes}, la courbe précédente contient beaucoup de points, comme par exemple \((i,0)\).
Mais surtout, en utilisant des nombres complexes, on relie la théorie des courbes à celle des surfaces.
Une courbe, par définition, est un objet de dimension 1, comme un cercle.
Un point sur la courbe est décrit par un seul nombre qui permet de le localiser, un angle sur un cercle.
Mais si ce nombre est un nombre complexe \(a+ib\) avec ses parties réelle et imaginaire, on se repère maintenant sur la courbe grâce à {deux} nombres réels, si bien que la courbe est devenue une surface !
C’est le coup de génie de Riemann : étudier les courbes (complexes) en observant que ce sont des surfaces (réelles).

Une surface de Riemann est donc une courbe algébrique, pensée comme étant une surface à deux dimensions réelles.

Même si cela n’est pas du tout évident, Riemann nous a montré qu’il faut penser à une courbe de la forme
\[
y^2 = x^3 + px + q
\]
comme une surface torique, comme ceci.

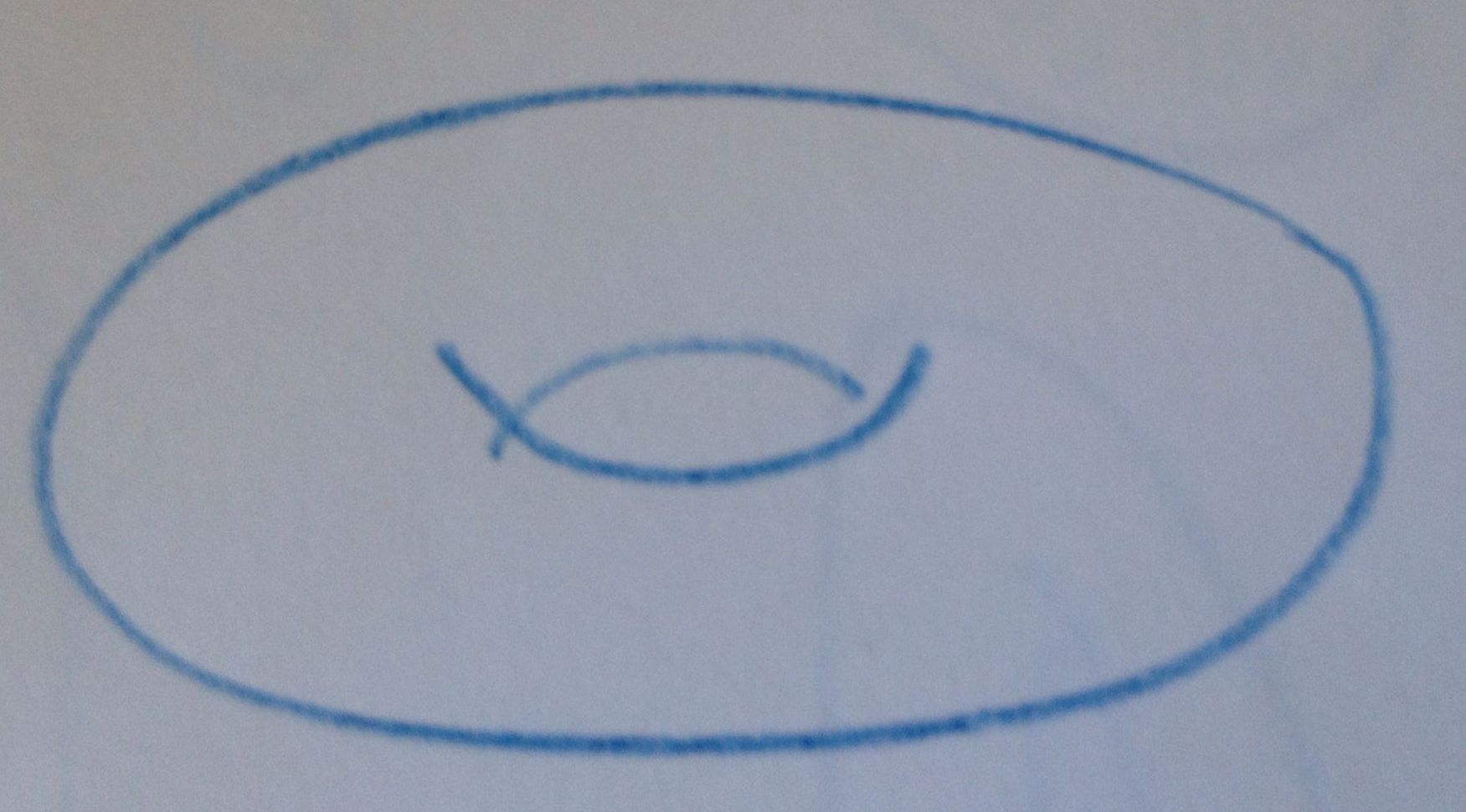
Une courbe de degré plus grand sera en général représentée par une surface dont la forme est plus compliquée.

Les choses deviennent plus intéressantes encore lorsqu’on fait varier les coefficients du polynôme qui définit la courbe, comme \(p\) et \(q\) dans l’exemple précédent.
La courbe/surface reste torique, elle se déforme continûment, mais sa géométrie varie.
Il y a beaucoup de géométries possibles sur un tore…

Une courbe algébrique, une surface de Riemann, fournit donc non seulement une forme mais aussi une géométrie.

L’espace des modules des surfaces de Riemann

L’une des grandes contributions de Riemann a été d’étudier les surfaces qui portent son nom, non pas comme des objets individuels, mais comme appartenant à des familles de surfaces se déduisant les unes des autres par déformations.
Ceci divise essentiellement les surfaces selon leur « genre » : le genre 0 correspond aux déformations de sphères, le genre 1 de tores,…
En général lorsque le genre est \(g\), la surface est obtenue à partir d’une sphère en lui recollant \(g\) « anses » comme sur cette figure.

L’ensemble de toutes les surfaces de Riemann dont le genre est \(g\) s’appelle « l’espace des modules des courbes de genre \(g\) ».
Chaque point de ce nouvel espace représente une surface de Riemann, un chemin dans cet espace une famille de surfaces se déformant continûment les unes dans les autres.
Pour être précis, il faudrait de longues pages compliquées, et en particulier, il faudrait expliquer clairement quand on considère que deux surfaces de Riemann sont « les mêmes ».
Je recommande le premier chapitre de ce livre, hélas au niveau master…

Un nombre impressionnant de travaux concernent l’espace des modules, depuis l’époque de Riemann jusqu’à ceux de Mirzakhani.
On sait par exemple qu’il s’agit d’un espace de dimension (complexe) \(3g-3\) qui possède une géométrie particulièrement intéressante.

Deux théorèmes de Mirzakhani

Partez d’une courbe de genre \(g\).
Il lui correspond donc une surface réelle \(S\).
Le « théorème d’uniformisation » (qui date de 1907) permet de définir sur \(S\) une géométrie homogène, plus jolie que les autres (à courbure constante).
En particulier, on peut mesurer la longueur d’une courbe tracée sur \(S\).

Choisissez une courbe fermée sur \(S\), comme par exemple la courbe orange sur cette figure :

Déformez la courbe de façon à en minimiser la longueur, un peu comme si la courbe initiale était un élastique sur la surface qui cherche à se contracter pour prendre une position d’équilibre.
Cette position d’équilibre s’appelle une géodésique fermée, la courbe foncée sur la figure.

Fixez maintenant un nombre \(L\) et cherchez à compter le nombre \(N(L)\) de géodésiques fermées sur \(S\) dont la longueur est inférieure à \(L\).
On sait depuis longtemps que \(N(L)\) croît très vite, exponentiellement vite.
De nombreux travaux étudient cette fonction.
Attention, \(N(L)\) compte toutes les géodésiques, y compris celles qui se recoupent elles-mêmes, comme la courbe orange de cette figure :

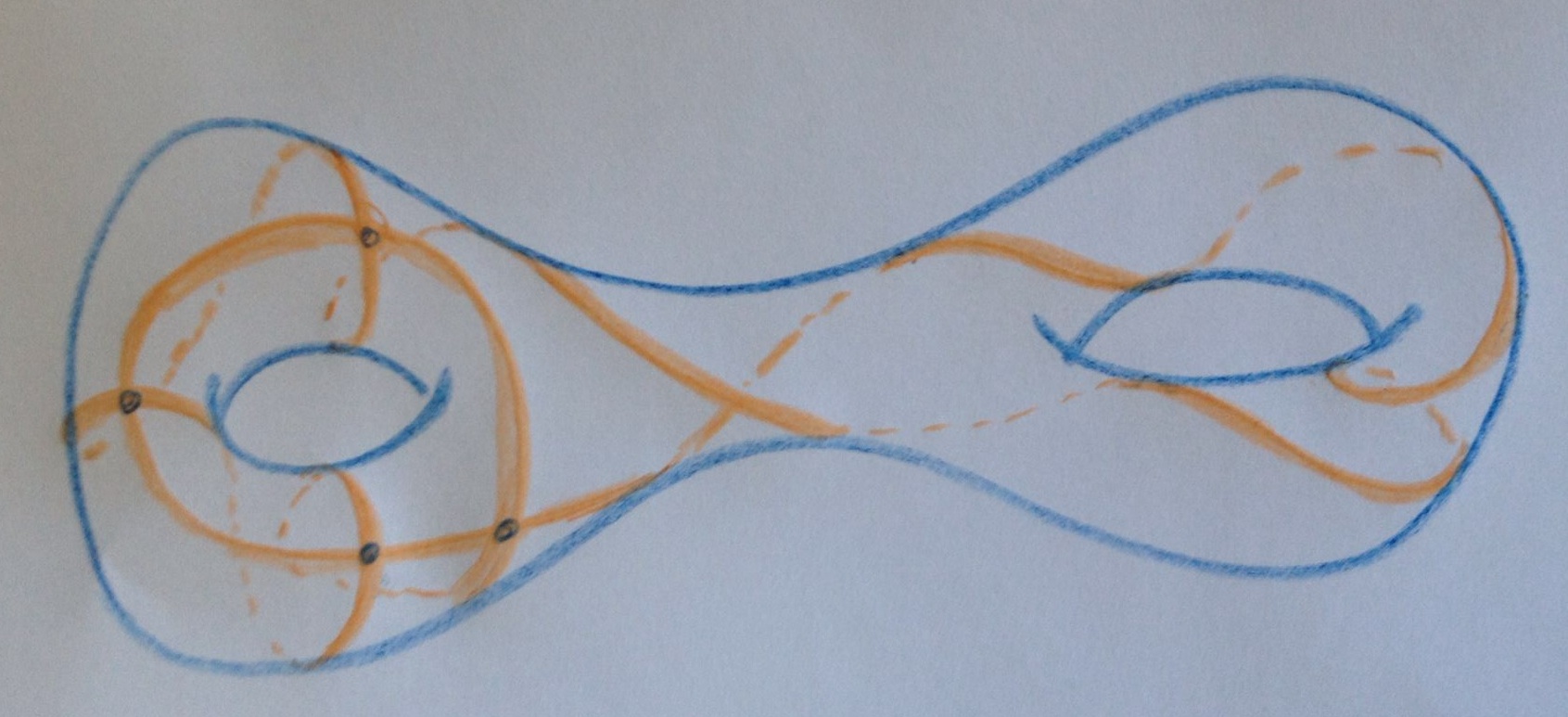
La thèse de Maryam Mirzakhani consistait à compter le nombre \(N_s(L)\) des géodésiques de longueur inférieure à \(L\) et qui sont simples, c’est-à-dire qui ne se recoupent pas entre elles.
Mirzakani montre cette fois que \(N_s(L)\) a une croissance beaucoup plus lente, équivalente en fait à un polynôme, qu’elle décrit très précisément.

Ce résultat, même s’il peut sembler technique, a des implications importantes à la fois pour la dynamique des billards et pour une meilleure compréhension de la forme de l’espace des modules (en donnant par exemple une preuve plus conceptuelle d’une conjecture de Witten).

Article édité par Étienne Ghys.