Une jolie exposition sur les mathématiques (et d’autres choses comme la cuisine) nous donne l’occasion de chercher quelques traces des mathématiques au bout du chemin de Saint-Jacques.
L’exposition itinérante Imaginary s’est arrêtée à Saint-Jacques-de-Compostelle du 18 mars au 16 mai 2013, à l’ancienne Église de l’Université (ou de la Compagnie comme elle était connue avant l’expulsion des Jésuites). Cette exposition, côtoyait une exposition photographique qui a suscité autant d’intérêt parmi les matheux que chez les profanes.
.
Intitulée Le goût des maths et sous le commissariat de la mathématicienne Mercedes Siles elle est l’œuvre d’un autre mathématicien Pedro Reyes. A l’occasion de l’exposition Imaginary à Málaga, celui-ci a photographié une douzaine de plats créés par le chef José Carlos García du Restaurant Café de París de Málaga et inspirés de quelques-unes des surfaces exhibées dans Imaginary. Géométrie et cuisine réunies dans une exposition savoureuse.
.
.
Presque par hasard, alors que je proposais un jeu à mon fils et un copain, je me suis rendu compte que des traces de mathématiques se multiplient autour de l’exposition, aussi bien dans la ville baroque que dans l’église même, présidée par le cercle radiant qui entoure le blason des jésuites et qui semble se projeter vers l’infini. 8 
.
.
Dans les chapelles latérales, des colonnes torses, ornées de grappes de raisin et feuilles de vigne comme il est toujours habituel dans le baroque galicien, cernent les retables. Quelques décennies avant que les jésuites s’installent à Saint-Jacques-de-Compostelle en 1577 et un siècle et demi avant la rénovation de l’ancienne église médiévale entre 1670 et 1673, Albrecht Dürer décrivait dans son livre Underweysung der messung un procédé pour construire de telles colonnes :
Underweysung der messung
Je me propose dans ce qui suit d’enseigner une deuxième colonne ronde, qui sera torse ou courbée d’une manière singulière.[…] Prise neuf fois, la grosseur de la colonne […] constituera la hauteur de la colonne […].
Et poses-en d’abord le plan dont tu dois extraire la colonne en la tordant. La colonne ci-dessus décrite étant dessinée, mène une ligne verticale en son milieu, a en bas et b en haut. Cette ligne ab doit être tirée du plan à la façon d’un limaçon. Ce plan, tu l’obtiendras comme suit. Décris autour d’un centre a un cercle correspondant à la grosseur de la colonne. Mène dans ce cercle une droite verticale passant par le centre a et traversant le cercle de part en part. Divise la moitié supérieure de cette ligne droite, comprise entre le centre a et la circonférence, par un point c en deux parties. Détermine ensuite sur cette ligne verticale, mais en dessous de a, un centre d, autour duquel tu décriras un cercle passant en haut par le point c et en bas par le point d’intersection de la verticale et de la grande circonférence. Divise ensuite la ligne droite ac par un point e en deux parties et décris autour de e une circonférence passant par c et a. Ceci étant effectué, gradue ces trois cercles en en numérotant les points de 1 à 60 et commence à compter 1, 2, 3, 4, 5, etc., à l’intérieur près de a. Compte de un à six dans le plus petit cercle, le numéro six coïncidant avec c. Continue alors de compter le long du cercle moyen, 7, 8, 9, etc., jusqu’à dix-huit, qui correspond a la demi-circonférence. Place alors le numéro dix-neuf sur la circonférence extérieure et continue de compter tout autour jusqu’à quarante-deux, numéro qui se trouvera en dessous de 18 sur la ligne verticale cead. Bifurque avec le numéro quarante-trois sur le cercle moyen jusqu’à ce que tu te trouves en c avec le numéro cinquante-quatre. Reviens alors avec le numéro cinquante-cinq dans le petit cercle jusqu’à ce que tu arrives au point a, qui coïncidera avec le numéro soixante. […] C’est à l’aide de ces points numérotés du plan abaissé qu’il convient de tordre la perche ou l’axe de la colonne verticale. Ce plan étant préparé, divise la colonne par soixante points numérotés selon sa longueur, mais d’une manière particulière, comme suit. Prolonge la ligne située à la base de la colonne […] horizontalement jusqu’à ce qu’elle dépasse la colonne d’une longueur double de sa grosseur […]. Désigne par f son extrémité. Mène une droite oblique issue de f jusqu’à l’extrémité supérieure de la colonne […]. Décris vers le haut un arc de cercle coupant la droite oblique, reliant f au sommet de la colonne […]. Ensuite, divise cet arc de cercle en soixante parties égales que tu numéroteras. Ensuite, mène des lignes droites issues de f, passant par les degrés de l’arc circulaire et allant jusqu’à la colonne. Mène des droites horizontales issues des points que tu auras ainsi obtenus sur la colonne, désigne-les par les numéros du plan abaissé […]. Tu verras que les divisions du fût de la colonne seront plus grandes au fur et à mesure que l’on monte.
Dessine une deuxième fois une ligne ab sur l’axe de la colonne, avec toutes ses lignes horizontales et ses numéros, puis prends un compas, va vers le plan circulaire qui doit servir à tordre l’axe et à en déplacer les points, pose une de ses pointes constamment sur la ligne droite coupant le plan circulaire en deux, puis prends dans l’ouverture du compas les distances horizontales des points numérotés, quel que soit l’ordre dans lequel ils se succèdent, et reporte ces distances vers l’axe ab de la colonne en posant une pointe du compas sur ab et la ligne horizontale portant le numéro correspondant à celui que tu as pris dans le plan circulaire. L’autre pointe du compas indiquera sur la même horizontale le lieu où se trouvera le point déplacé de l’axe tors […].Tu verras de la sorte de part et d’autre de l’axe droit apparaître en pointillé l’axe courbe de la colonne torse […]. Prends alors un compas et reporte la grosseur de la colonne de l’axe droit de la première colonne considérée avec toutes ses horizontales vers l’axe tors […]. Décris sur ces dernières des circonférences et tu auras ainsi trouvé la grosseur de la colonne […]. Même si la colonne circulaire est courbe, on pourra continuer à imaginer en elle de telles sphères, qui peuvent être divisées en deux par les sections imaginées précédemment et qui ont leur centre sur l’axe […]. Considère maintenant et imagine que chaque point de l’axe tors de la colonne est le centre d’une sphère. Décris alors sur la ligne transversale passant par ce point un cercle égal à la grosseur de la colonne droite à la même hauteur. Procède ainsi avec tous les points de l’axe de la colonne torse. Tu obtiendras la grosseur de la colonne dans toutes ses sinuosités. Tous ces cercles étant tracés, relie toutes leurs circonférences par une ligne continue et tu verras apparaître la forme de la colonne. 9Albrecht Dürer, Géométrie. Présent., trad. de l’allemand et notes par Jeanne Peiffer. Seuil, Paris, 1995.
Dürer commence par construire une courbe plane qui consiste à parcourir trois cercles dont les diamètres du deuxième et du troisième cercle sont 3/4 et 1/4 du diamètre du premier cercle.
- Plan abaissé (Image animée à ouvrir avec Adobe Reader).
- durero-animate-1-wp
Il remplace ensuite cette courbe plane par une courbe gauche dont la troisième coordonnée du point d’étiquette \(n\) est donnée par
\[2 \, b \, \tan ( n \arctan ( \frac 9 2 ) / 60)\]
où \(b\) est le diamètre de la base de la colonne et \(\arctan( \frac 9 2 )\) a une valeur approchée au centième par défaut de 77,47º. Le facteur 9 qui mesure le rapport entre la hauteur de la colonne et le diamètre de la base est lié au canon à propos des ordres en architecture 10En réalité, il faudrait parler de canons aussi bien pour la stature des hommes que pour les différents ordres en architecture. À la diversité des canons classiques, déjà reconnue par Vitruve dans son fameux traité De architectura, il faut ajouter la persistance du canon médiéval, dit « de Varron », qui influencera Dürer à travers l’oeuvre De sculptura (1504) de Pomponius Gauricus, voir l’édition annotée et traduite par André Chastel et Robert Klein, Libraire Droz, Genève, 1969. On trouve le même rapport 1/9 dans le traité Medidas del Romano (1526) de l’espagnol Diego de Segredo, très influencé par Dürer. L’image provient d’une traduction française de 1550 conservée à l’INHA.
. Le procédé d’élévation de la courbe plane est illustré par Dürer dans la figure suivante 11Source Gallica. (accompagnée ici d’une petite animation) :
.
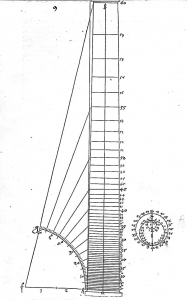
- Élévation (Image animée à ouvrir avec Adobe Reader)
- durero-animate-2-wp
Pour conclure, il trace enfin une sphère de diamètre \(b\) autour de chaque point de la courbe gauche ainsi obtenue, voir la figure ci-dessous.
- Colonne torse (Image animée à ouvrir avec Adobe Reader).
- durero-animate-3-wp
Bien plus tard, dans les feuilles distribuées 12Complétées sous le titre de Applications de l’Analyse à la géométrie en 1807. Voir l’introduction L’invention d’une langue des figures de Bruno Belhoste et René Taton aux Leçons de Monge dans le volume L’École normale de l’an III. Leçons de mathématiques, Jean Dhombres (dir.), Éditions Rue d’Ulm, 1992. aux étudiants de son cours d’analyse appliquée à la géométrie de l’an III à l’École centrale de travaux publiques 13Renommée « École Polytechnique » à partir du 15 fructidor an III (1er septembre 1795)., Gaspard Monge s’intéresse à un certain type de surfaces :
Application de l’Analyse à la geómétrie
Une courbe quelconque étant tracée sur le plan horizontal, si l’on imagine qu’une sphère d’un rayon constant se meuve de manière que son centre suive la courbe, elle parcourra un espace qui sera enveloppé par une certaine surface courbe. Cela posé, trouver, 1º l’équation générale de toutes les surfaces courbes soumises à cette génération, quelle que soit d’ailleurs la courbe plane qui leur sert d’axe ; 2º les équations de la caractéristique de ces surfaces ; 3º celle de leur arête de rebroussement.
1º La surface que nous considérons étant l’enveloppe d’une suite de sphères de même rayon, il est évident que son plan tangent coïncide avec le plan tangent de la sphère enveloppée qui la touche au même point. […]
Autrement. Il est évident que toutes les normales de l’enveloppe coupent la courbe qui lui sert d’axe, et que les parties de ces normales comprises entre la surface et le plan horizontal sont égales entre elles et au rayon des sphères enveloppées. […]
2º La caractéristique de la surface, c’est-à-dire la courbe de contact de cette surface avec chacune des enveloppées, est évidemment, dans ce cas, la ligne de plus grande pente de la surface, ou, ce qui revient au même, elle est, de toutes les courbes qui sont sur la surface et qui passent par un même point, celle dont la tangente en ce point fait le plus grand angle avec le plan horizontal. […]
3º L’arête de rebroussement de la surface touche en chacun de ses points une de ses caractéristiques ; ces deux courbes ont donc en ce point une tangente commune : donc la tangente de l’arête de rebroussement par un point de contact pris à une certaine hauteur, fait avec le plan horizontal le même angle que la tangente de la caractéristique pour un point de contact pris à la même hauteur. 14Gaspard Monge, Application de l’Analyse à la geómétrie. Cinquième édition, revue, corrigée et annotée par M. Liouville. Bachelier Imprimeur, Paris, 1850. Source Internet Archive.
Monge les appelle « surfaces de canaux », un nom qu’on applique aujourd´hui aux enveloppes d’une famille de sphères dont les centres appartiennent à une courbe gauche. En outre que les hélicoïdes cerclés et les colonnes torses de Dürer (dont le rayon des sphères est constant), on y trouve les surfaces de révolution et les cyclides de Dupin non paraboliques. Dans la figure ci-dessous, on montre une colonne torse de Dürer dont le rapport entre le diamètre de la base et la hauteur est égal à \(1 /4\sqrt{3}\).
- Une autre colonne torse (Image animée à ouvrir avec Adobe Reader).
- durero60-animate-wp
ÉCRIT PAR
Fernando Alcade
Mathématicien - Saint-Jacques de Compostelle
