Mathempsycose

La Mathempsycose n’est ni une maladie mentale, ni la réincarnation d’un concept.

La mathempsycose, telle que je la définis est plutôt l’incarnation d’un concept mathématique ; ou bien encore l’incorporation, l’appropriation que tout un chacun, pour peu qu’il soit sensible aux mathématiques, se fait d’un concept mathématique. Qui a été sensible, dans son enfance ou sa jeunesse, aux mathématiques a certainement plusieurs exemples d’émerveillement devant un élément ou une notion mathématique bien abstraite.

Personnellement, je sais qu’il ne m’est pas possible de séparer le plaisir de jouer avec les concepts abstraits mathématiques, du plaisir visuel des images qui y sont associées. C’est sans doute une des raisons qui expliquent que je sois devenu plasticien en gardant toujours un œil dans le colis-matheur. Les mathématiques sont une science humaine, dans le sens qu’elle est portée, soutenue par des êtres sensibles. Bien évidemment les sensibilités sont diverses, multiples et conduisent dans des voies aux directions variées. Les voies empruntées peuvent rendre difficile la perception de l’origine et de l’étayage mathématique qui les accompagne.

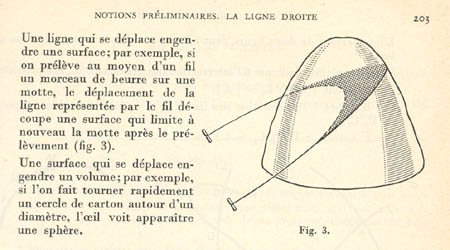
Pour exemple je prendrai le cas de l’angle droit. Il est certain que j’ai pris autant de plaisir à découvrir, enfant, la géométrie qu’à manipuler les règles, les équerres, les compas et découvrir les images, avec la typographie qui y étaient associées, dans les livres de classe. Je sais maintenant que je n’aurai pu me satisfaire de manipuler des concepts mais qu’il était merveilleux de pouvoir associer une réflexion à un plaisir de l’œil ou des sens. Quelle joie, et aussi quel étonnement, quand on m’apprit que l’on pouvait inscrire plusieurs triangles rectangles (de même hypoténuse) dans un demi-cercle (dont le diamètre, etc.). Quoi ? deux objets de nature différente se tendaient la main ? … Je pourrais m’étendre presque à l’infini sur de tels émerveillements.

Si mon inclination personnelle m’a conduit à apprécier et m’intéresser aux drapés en peinture ⁴ voir l’article d’Etienne Ghys consacré aux plis et fronces, je garde en mémoire, comme celui qui m’a le plus touché, celui qui est présenté dans la petite Cène de Philippe de Champaigne au Louvre. Il n’est pas nécessaire d’épiloguer, il suffit de regarder l’image ci-dessus. J’y retrouvais des angles droits … incarnés : une simplicité, mais quelle pureté ! Du reste de la peinture je ne gardais guère de souvenir particulier. ⁵Je dois avouer que bien longtemps avant d’avoir vu cette peinture, comme j’avais été enfant de chœur, j’avais été impressionné par ce tissu blanc que je dépliais pour couvrir le maître autel. Il était plié de manière impeccable et gardait les traces de ces plis orthogonaux une fois étalé. Je dirais que je trouvais cela aussi beau qu’un théorème dans sa rigueur et sa simplicité… une fois démontré ! Ce rapprochement subit de deux choses aussi éloignées pourrait sembler extravagante ou forcée. Je pense être sincère, car c’est bien ainsi que j’ai vécu et continue à vivre ma relation aux mathématiques

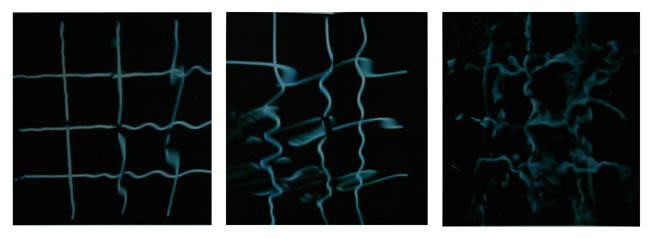
Poursuivant dans cette lignée de l’angle droit et/ou du carré, je garde également en mémoire ces reflets déformés, dans l’eau, d’une trame qu’a réalisé François Morellet. La forme figée et connue du carré qui se met à vibrer de façon aléatoire.

Plus troublante ou dérangeante, car je ne saurais trop me l’expliquer, est l’appropriation que Piet Mondrian s’est fait de l’angle droit. Sans doute est-ce lié à la charge spirituelle qu’il y mettait et qui se dégage lorsqu’on se trouve face aux originaux.

Un dernier exemple tout aussi troublant est le Carré blanc sur fond blanc de Kasimir Malevitch. ⁶Il a utilisé deux blancs d’origines différentes : française pour le carré, russe pour le fond Juste un petit doigt de plus qu’une abstraction pure. La limite aurait été atteinte par l’artiste conceptuel Lawrence Weiner, dont le travail consiste à écrire des phrases, … s’il avait écrit cette expression : UN CARRÉ BLANC SUR FOND BLANC … mais c’était trop tard.