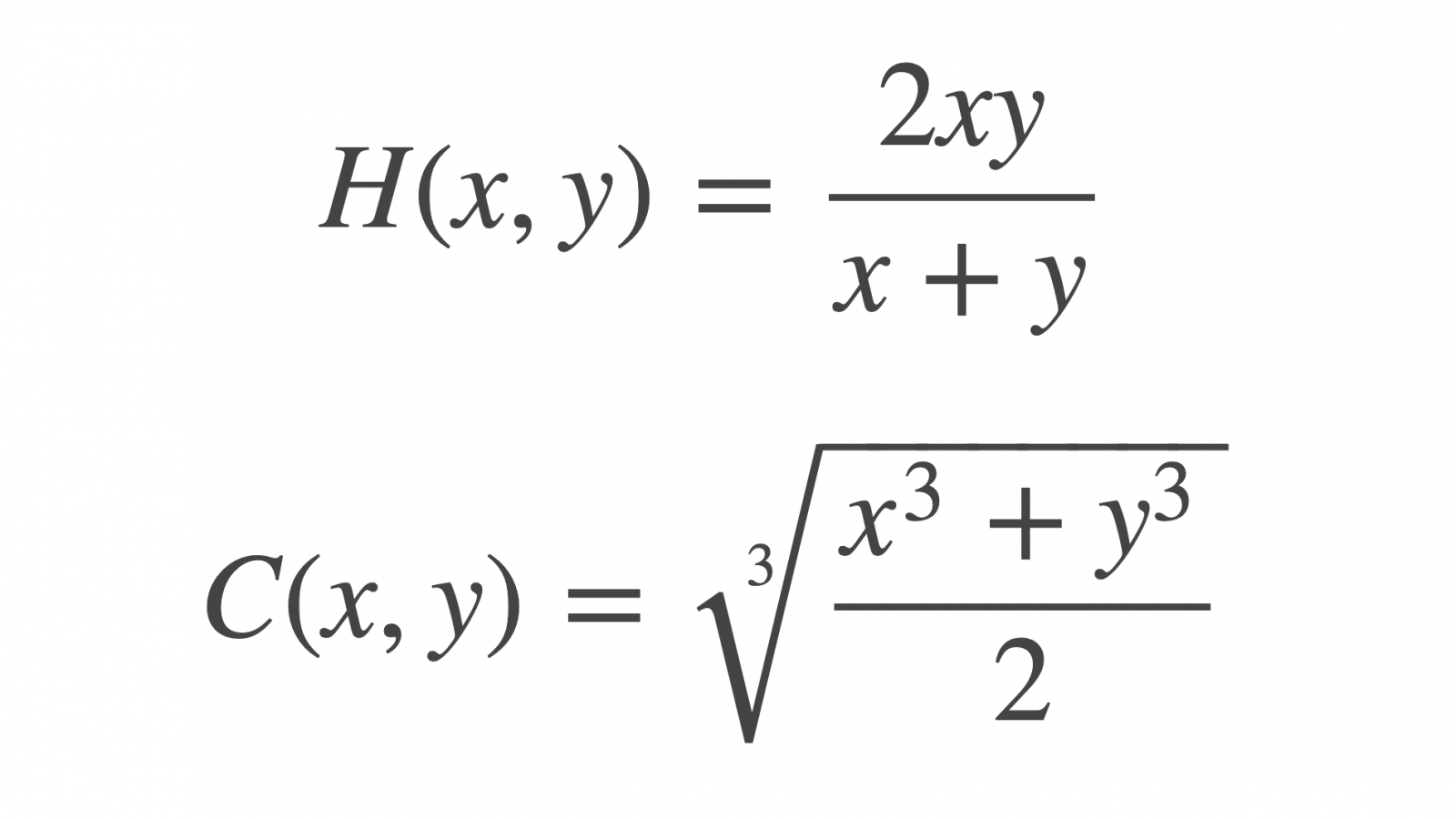
Tout le monde sait ce qu’est la moyenne de plusieurs nombres, ne serait-ce que pour y avoir été confronté lors de sa scolarité. Toutefois, il est moins connu qu’il existe d’autres notions de moyenne. Bien sûr, il y a des moyennes pondérées, qui donnent un poids différent aux nombres considérés (les fameux coefficients qui diffèrent entre un devoir à la maison et un devoir sur table), mais je veux parler ici de moyennes radicalement différentes, au moins à première vue.
Quelques exemples
Commençons par décrire quelques exemple de moyennes. Pour cela, on va donner des formules, mais elles ne sont pas trop compliquées. Si elles vous semblent mystérieuses à première vue, ça tombe bien : mon objectif est de les démystifier ensuite !
Notons \(x\) et \(y\) deux nombres dont on veut calculer la moyenne ; chacune des formules ci-dessous a une généralisation à autant de nombres que souhaité, mais se contenter de deux nombres permet de garder des formules légères.

.
La moyenne arithmétique est donc la moyenne « toute bête ». Remarquons qu’on pourrait compléter ce tableau avec des moyennes du même type que les moyennes quadratique et cubique, en passant aux degrés 4, 5, etc. Nous allons voir qu’on peut même généraliser beaucoup plus que ça.
On peut se demander en quoi les formules précédentes méritent le nom de « moyenne ». Le premier élément de réponse vient de certaines propriétés
particulières qu’elles vérifient. On attend en particulier d’une moyenne \(M\) que \(M(x,y)\) soit toujours entre \(x\) et \(y\), que \(M(x,x)=x\), et
que \(M(x,y)\) soit croissante en chacune des deux variables, c’est-à-dire qu’elle augmente si l’on augmente \(x\) sans bouger \(y\) ou si l’on augmente
\(y\) sans bouger \(x\). On peut facilement vérifier que toutes les moyennes ci-dessus satisfont à ces propriétés, à condition parfois de restreindre
le choix de \(x\) et \(y\). Par exemple, la moyenne arithmétique vérifie les propriétés voulues pour tous \(x\) et \(y\), alors que la moyenne quadratique ne les vérifie que pour \(x\) et \(y\) positifs ou nuls. La moyenne géométrique n’est même pas définie si par exemple \(x>0\) et \(y<0\). À chaque moyenne correspond un certain intervalle de définition ; nous y reviendrons.
Mais il y a un lien bien plus fort entre elles. Regardons par exemple comment est construite la moyenne quadratique : on prend les deux nombres \(x\) et \(y\),
on les met au carré, on fait la moyenne arithmétique de ces carrés et on passe à la racine carrée. On a donc combiné la moyenne arithmétique avec une fonction,
en l’occurrence la fonction \(x\mapsto x^2\) et son inverse. Cette façon de combiner avec une fonction « en aller-retour » s’appelle en mathématique « conjuguer », ou parfois « tirer en arrière » [[Qui est une traduction assez inélégante de l’expression anglaise « to pull back ».]] suivant le contexte.
On peut construire de la même façon toutes les moyennes ci-dessus, en remplaçant la mise au carré par d’autres fonctions. Il faut choisir des fonctions
inversibles, comme \(x\mapsto x^2\) dont l’inverse est \(x\mapsto \sqrt{x}\), {vues commes fonctions de \([0,+\infty[\) dans lui-même}.
C’est là qu’apparaît clairement l’intervalle de définition : la fonction \(x\mapsto x^2\) n’est
pas inversible de \(]-\infty,+\infty[\) sur \([0,+\infty[\), puisque par exemple le nombre \(1\) est obtenu comme l’image de \(1\) et de \(-1\).
Voici les fonctions qui permettent de retrouver les différentes moyennes qu’on a vues et les intervalles de définition associés.

.
Ce point de vue permet très facilement de définir les moyennes géométriques, harmoniques, etc. de plus de deux nombres, puisqu’il nous ramène à la moyenne arithmétique. Par exemple, pour calculer
la moyenne harmonique de trois nombres strictements positifs \(x\), \(y\) et \(z\), on fait la moyenne de leur inverse et on en prend l’inverse (car \(x\mapsto 1/x\) est sa propre réciproque), ce qui donne
\[H(x,y,z)=\frac{1}{\frac13 \left(\frac1x+\frac1y+\frac1z\right)}.\]
En réduisant au même dénominateur, on peut exprimer cette moyenne sous la forme
\[H(x,y,z)=\frac{3xyz}{yz+xz+xy}.\]
On peut aussi très facilement définir des moyennes pondérées pour la même raison. Par exemple, a moyenne quadratique de \(x\) avec coefficient \(2\) et \(y\) avec coefficient \(3\)
est
\[\sqrt{\frac{2x^2+3y^2}5}.\]
Dans un prochain billet on verra ces différentes moyennes un peu plus en détail, et on essaiera de les interpréter. L’objectif sera le suivant : montrer que parfois, la moyenne arithmétique n’est pas pertinente mais que souvent, on peut trouver une moyenne différente qui l’est.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.