Moyennes (III) : la moyenne géométrique

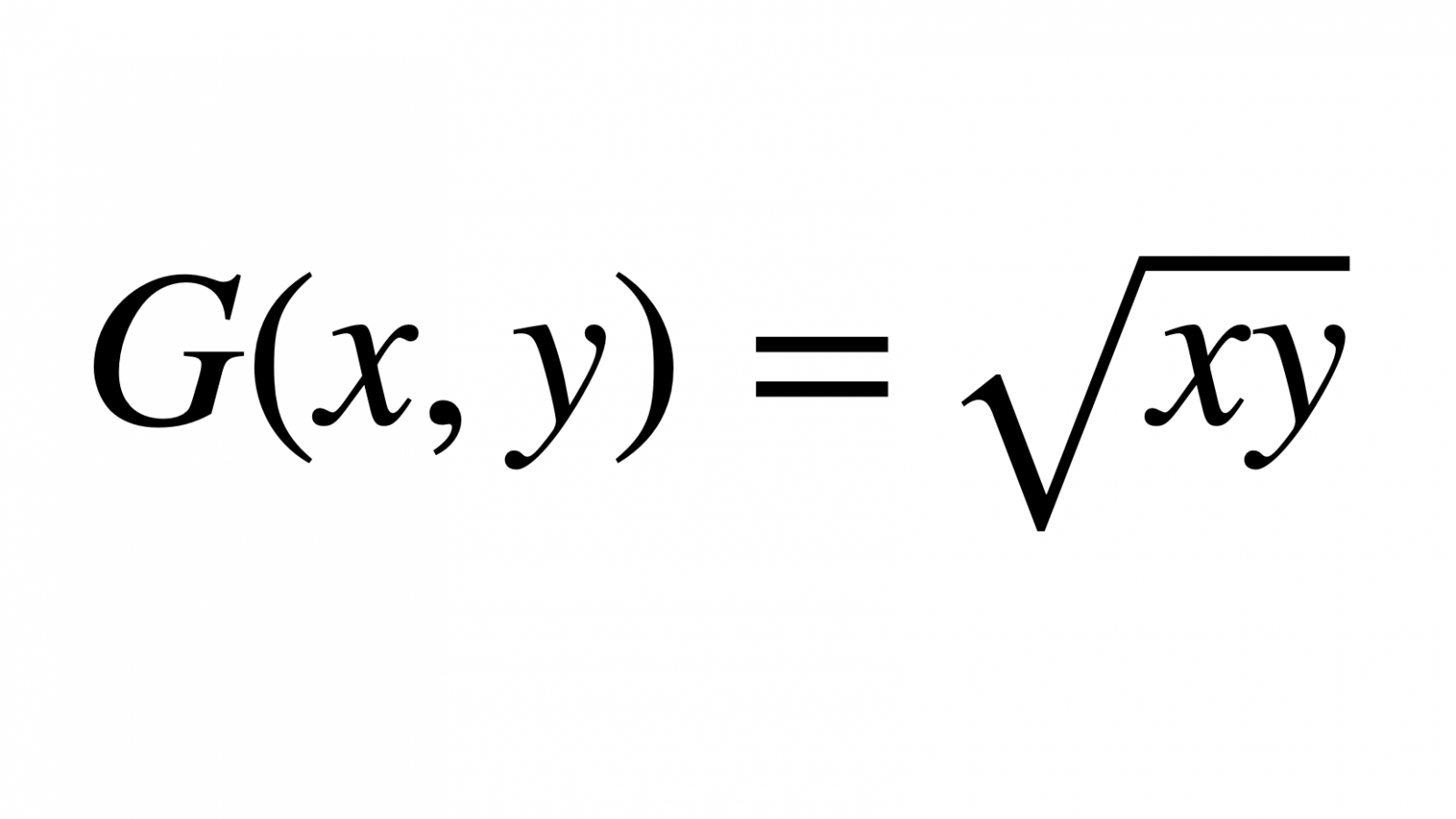
Ce billet est le troisième d’une série commencée ici et là. Nous allons discuter plus en détail la moyenne géométrique, et traiter par l’exemple la construction d’une moyenne ad hoc. Comme la méthode doit commencer à être familière, ce billet est sans doute le dernier de la série, en tout cas dans l’étude de moyennes individuelles.

Définition de la moyenne géométrique

La moyenne géométrique est définie pour deux nombres positifs par
\[G(x,y)=\sqrt{xy}\]
et en général par
\[G(x_1,x_2,\ldots,x_n)=\sqrt[n]{x_1x_2x\cdots,x_n}.\]
Pour éviter les formules plus compliquées, je ne parle pas des moyennes pondérées, mais elle existent bien sûr.

J’ai signalé dans le premier billet qu’elle était obtenue en conjuguant la moyenne arithmétique par le logarithme ; voyons ça d’un peu plus près.

Plutôt que de rappeler en détail ce qu’est le logarithme (voir par exemple la
[wikipédia->http://fr.wikipedia.org/wiki/Logarithme]), je vais me limiter aux propriétés essentielles dont j’aurai besoin, à savoir :
\[\log(xy)=\log(x)+\log(y)\]
et sa jumelle
\[\log(x^k)=k\log(x).\]
Dans ces formules, \(x\) représente n’importe quel nombre strictement positif et \(k\) n’importe quel nombre réel. Par exemple, comme la racine carrée d’un nombre est en fait sa puissance \(1/2\), on a
\[\log(\sqrt{x})=\frac12\log(x).\]
Une petite remarque : il y a en fait plusieurs logarithmes, qui partagent ces propriétés, mais tous mènent à la même moyenne géométrique. On en choisit donc un une fois pour toute, et on l’appelle « le » logarithme.

Si on applique la méthode habituelle pour construire une moyenne, on commence avec deux nombres (strictement positifs) \(x\) et \(y\), et on considère la moyenne arithmétique de leurs logarithmes :
\[\frac{\log(x)+\log(y)}2=\frac12 \log(xy)=\log(\sqrt{xy}).\]
Ensuite, on applique l’inverse du logarithme (qui est une exponentielle, mais on n’a pas besoin de savoir grand-chose à part son existence !) pour obtenir \(G(x,y)=\sqrt{xy}\). La même méthode
mène à la moyenne géométrique de plusieurs nombres. En fait, tout ça n’est pas surprenant : la formule de \(G\) est la même que celle de la moyenne arithmétique en changeant les additions
en multiplications est les divisions en racines. Comme le logarithme « échange » ces opérations,il conjugue tout naturellement les deux moyennes.

 

Application à l'inflation

La moyenne géométrique n’est pas un objet gratuit : elle intervient très naturellement dès que l’on considère des nombres qui se multiplient plus qu’ils ne s’additionnent. Un exemple très simple est celui de l’inflation : imaginons que l’inflation (c’est-à-dire la hausse des prix ³En fait, il s’agit d’une hausse moyenne. À votre avis, quelle moyenne est utilisée ? Et, plus fin, quelle pondération considère-t-on ?) soit de \(1\%\) en 2010 et de \(3\%\) en 2011. Quelle est l’inflation moyenne sur ces deux années ?

Bien sûr, comme tout dépend de la définition, on peut imaginer considérer la moyenne arithmétique
et répondre que l’inflation moyenne est de \(2\%\). Mais quel sens cela a-t-il ? Personnellement,
je n’en vois aucun. Un choix naturel est de définir l’inflation moyenne comme celle qui, en deux ans,
produit le même effet que l’inflation réelle. Pour pouvoir se servir de cette définition, il faut se rappeler qu’une inflation de \(1\%\) correspond à une multiplication des prix par \(1+1/100=1,01\), une inflation de \(3\%\) à une multiplication par \(1+3/100=1,03\) et ainsi de suite : le prix est augmenté de un (ou trois) centième de lui-même.

Ainsi, si on note \(m\%\) l’inflation moyenne cherchée, on doit avoir : \[(1+m/100)(1+m/100)=1,01\times 1,03\] le membre de gauche donne le coefficient par lequel sont multipliés les prix en deux ans d’inflation constante à \(m\%\), et le membre de droite est le coefficient par lequel les prix ont réellement augmenté entre début 2010 et fin 2011.

Mais la formule ci-dessus se réécrit \(1+m/100=\sqrt{1,01\times 1,03}=G(1,01;1,03)\), et on voit arriver la moyenne géométrique.

En effectuant un calcul approché, on trouve \(m \simeq 1,01995\)~: l’inflation moyenne est d’environ \(1,995\%\), légèrement plus basse que la moyenne arithmétique (ce qui est dû à la concavité et à la croissance du logarithme).⁴La version initiale de ce billet contenait une erreur assez grossière~: en effectuant le mauvais calcul, j’étais tombé sur la valeur \(1,5\%\). Comme indiqué par un éminent collègue, il suffit d’effectuer un calcul au premier ordre~: \((1+m/100)^2\) est de l’ordre de \(1+2m/100\) et \((1+1/100)(1+3/100)\) de l’ordre de \(1+4/100\) avec dans les deux cas une erreur qui se compte en dix-millièmes. La valeur cherchée ne peut donc pas être très éloignée de \(2\). Alors que je tanne mes étudiants pour qu’ils vérifient leurs calculs par ce genre de méthode, me voilà bien arrosé.

Une moyenne plus pratique}

Dans l’exemple ci-dessus, j’ai un peu triché : la moyenne géométrique est appliquée aux coefficients par lesquels les prix sont multipliés, et pas au taux d’inflation exprimé en pourcents. Mais il est facile d’y remédier, puisque les deux grandeurs sont reliées par la fonction
\[f:\begin{array}{rcl}
]-100,+\infty[ &\to& ]0,+\infty[ \\
x &\mapsto& 1+\frac{x}{100}
\end{array}\]
On aura besoin de sa fonction inverse :
\[g:\begin{array}{rcl}
]0,+\infty[ &\to& ]-100,+\infty[ \\
z &\mapsto& 100(z-1)
\end{array}\]

Construisons donc une moyenne « des taux » \(T\) en conjuguant \(G\) par \(f\). La moyenne
de deux taux \(x\) et \(y\) (qui représentent des pourcentages) est obtenue en prenant leur image par \(f\):
\[1+\frac{x}{100}\quad\mbox{et}\quad 1+\frac{y}{100},\]
en faisant leur moyenne géométrique :
\[\sqrt{\left(1+\frac{x}{100}\right)\left(1+\frac{y}{100}\right)}=\sqrt{1+\frac{x+y}{100}+\frac{xy}{10\,000}}\]
et en en prenant l’image inverse par \(f\) :
\[T(x,y)=100\left(\sqrt{1+\frac{x+y}{100}+\frac{xy}{10\,000}}-1\right).\]
Voilà notre nouvelle moyenne. Pour chaque situation, on peut de la même façon en identifiant
la grandeur qui s’additionne (ou, en passant par la moyenne géométrique, se multiplie), fabriquer
une moyenne sur mesure.

Donnons pour finir la formule pour la moyenne d’un plus grand nombre de taux, (il vaut alors mieux garder la formule factorisée) :
\[T(x_1,x_2,\ldots,x_n)=100\left(\sqrt[n]{\left(1+\frac{x_1}{100}\right)\left(1+\frac{x_2}{100}\right)\cdots
\left(1+\frac{x_n}{100}\right)}-1\right).\]
En exercice, on peut chercher la formule pour une moyenne pondérée (elle n’est pas beaucoup plus compliquée, il suffit d’insérer les coefficients aux bons endroits).