Multiplier ou diviser par l’abscisse, à la main !

En appliquant une transformation simple à effectuer point par point avec une règle graduée, on peut facilement construire le graphe de \( x\mapsto xf(x)\), ou de \(x\mapsto f(x)/x\), à partir de celui de \( f\).

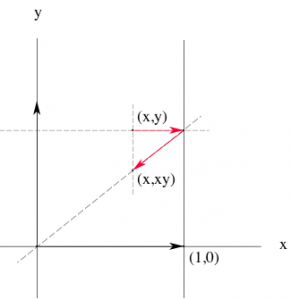
La multiplication par l’abscisse est décrite sur la figure suivante, suffisamment explicite me semble-t-il pour ne pas devoir préciser davantage les choses :

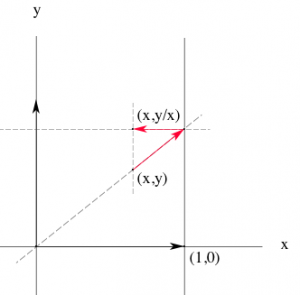
La transformation réciproque, la division par l’abscisse, s’obtient très facilement. La voici présentée sur un dessin :

En plaçant le point de coordonnées \( (x,y)\) dans les différents quadrants, ou de part et d’autre de la verticale d’équation \( x=1\), ces transformations permettent de visualiser de façon très claire la «règle des signes» ainsi que l’effet sur le module de la multiplication par un nombre plus grand ou plus petit que 1.

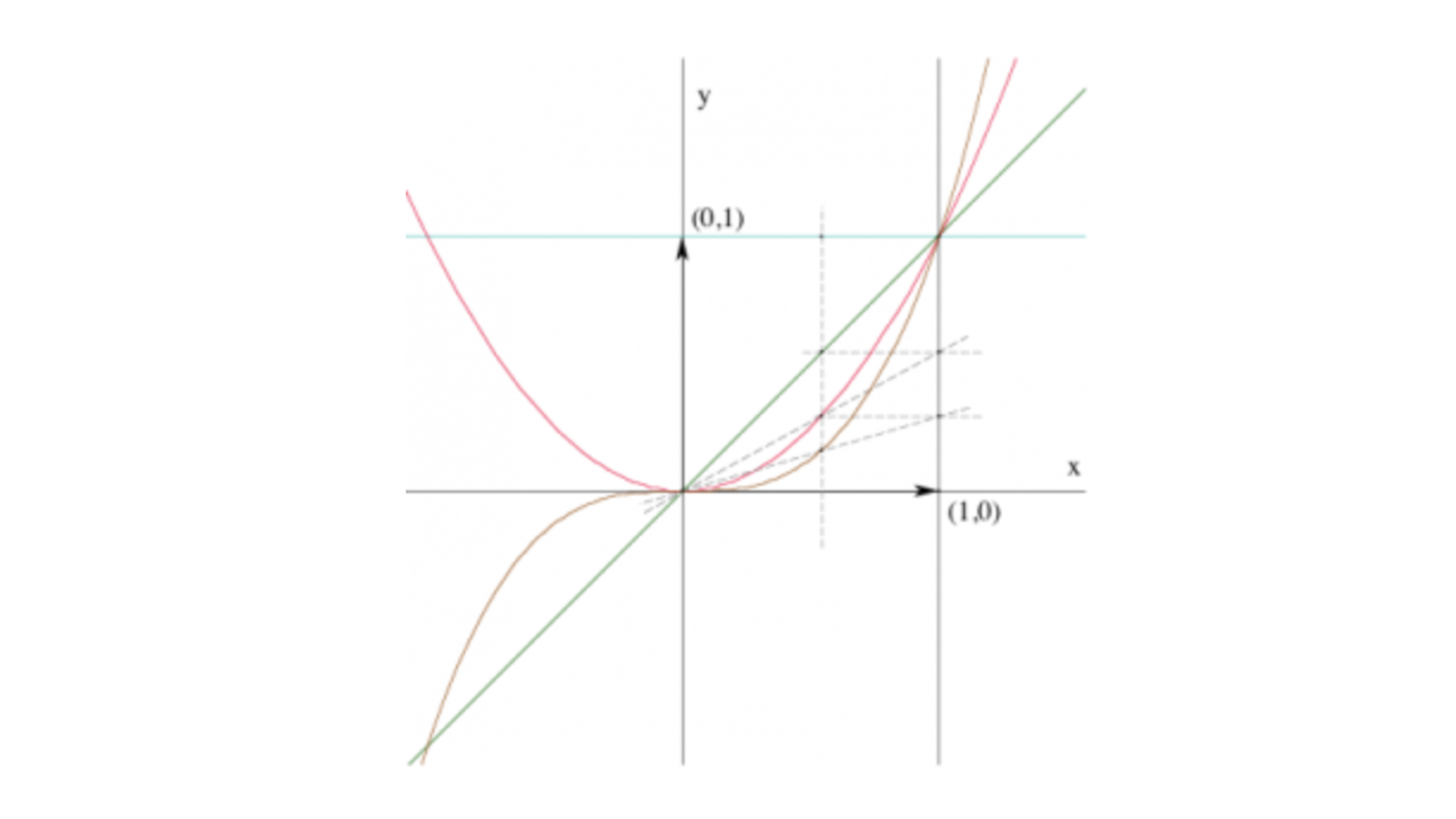
En itérant la multiplication par l’abscisse à partir du graphe de la fonction constante 1, on obtient ainsi facilement autant de point qu’on le souhaite des graphes des puissances entières et positives de \(x\). Sur cette figure, on a représenté les trois premières :

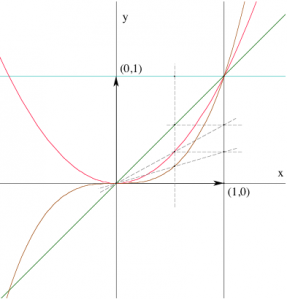
Pour les puissances négatives, et en particulier pour obtenir des points de l’hyperbole d’équation \( xy=1\), il suffirait d’itérer la seconde transformation.

On peut généraliser de diverses manières les deux transformations et obtenir de beaux graphes de polynômes. Voici un exemple dans lequel, au départ d’une droite, on obtient une parabole, une cubique et une quartique. Dans cet exemple, le rôle de l’origine dans les transformations originales est tenu par un point quelconque de l’axe vertical.

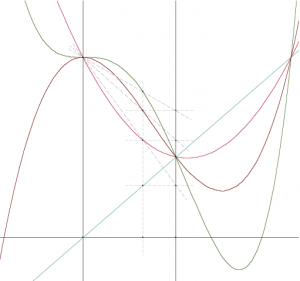
Les transformations présentées ici sont des cas particuliers {d’hyperbolisme} et {d’anti-hyperbolisme}. Ceux-ci donnent naissance à une multitude de courbes célèbres, dont la «Sorcière d’Agnesi» via laquelle j’ai fait leur connaissance.

Vous trouverez facilement sur le net des renseignements sur ces transformations, en visitant par exemple [cet excellent site ->