
Ce texte a été préparé pour une conférence à l’Académie des sciences pour la Semaine des mathématiques 2017, dans le cadre d’une action proposée par l’académie de Paris.
“\(92+9=103\)” (sic) se lit de la même façon partout, cela mérite commentaire. Tout le monde connaît la définition d’une sphère, cela mérite un commentaire encore plus étendu. D’où viennent les concepts mathématiques et les termes qui les expriment ? On en discutera, on en verra plusieurs exemples, dont celui des fractales. En passant, on ne s’interdira pas des observations, des constructions et des preuves.
C’est pour moi une joie de voir tant de lycéens dans cette salle des séances de l’Académie des sciences. Déjà mardi dernier, l’Académie avait accueilli sous la Coupole 140 lycéens, mais alors c’était du même lycée, le lycée Condorcet. Ils étaient venus participer à une séance consacrée à Condorcet. Condorcet est un grand philosophe du 18e siècle, qui s’est beaucoup occupé d’éducation. Dans l’un de ses discours il dit ceci :
« Les premières notions mathématiques doivent faire partie de l’éducation de l’enfance. Les chiffres, les lignes parlent plus qu’on ne croit à leur imagination, et c’est un moyen sûr de l’exercer sans l’égarer. »
Les chiffres, ce sont les nombres. Les lignes, ce sont les figures. Nombres et figures, c’est justement ce dont je veux vous entretenir tout de suite.
D’abord les nombres. Deux mille dix sept s’écrit en français avec seize lettres et trois trous entre les lettres, soit dix-neuf signes. Avec l’écriture décimale : 2, 0, 1, 7, quatre signes, tout le monde comprend, c’est une économie d’écriture et une économie de pensée. Comme plaisanterie, j’ai proposé dans le résumé de cette conférence la formule [92 + 9 = 103.]
L’important est que tout le monde la comprend de la même façon, quelle que soit la langue où on la prononce. Ce n’est pas parce qu’elle est fausse que je l’ai écrite, mais parce que tout le monde voit qu’elle est fausse.
L’écriture décimale est une langue universelle.
Et pourtant, il y a bien d’autres façons d’écrire les nombres, vous le savez bien : l’écriture duodécimale, à base douze, ou l’écriture binaire, à base deux, en sont des exemples. Le choix de la base dix a été celui des Chinois depuis la plus haute antiquité, et celui des savants européens depuis le Flamand Simon Stevin, au 16e siècle, et enfin celui des Français depuis la Révolution et l’adoption du système métrique. La première leçon du grand mathématicien Laplace à l’École normale de l’An III, l’ancêtre de l’École normale supérieure, est consacrée à la numération décimale et à sa comparaison avec d’autres systèmes de numération, en particulier la numération binaire. Aujourd’hui la numération binaire est essentielle en informatique et elle joue donc un rôle central dans notre existence, la numération à base douze existe encore dans certains commerces, la base soixante est utilisée dans la mesure des angles et dans la mesure des temps.
Ainsi l’universalité de la numération décimale est un phénomène historique, et je voudrais vous montrer que les mathématiques que nous pratiquons sont un résultat de l’histoire, même si elles nous apparaissent comme la révélation de vérités éternelles.
Qu’en est-il de la notion de nombre, indépendamment de leur écriture? Il n’y a pas de réponse mathématique à cette question. On peut l’esquiver en donnant un nom, une lettre, à l’ensemble de tous des nombres entiers. Si on l’appelle \(\mathbf{N}\), les nombres entiers sont les éléments de \(\mathbf{N}\).
Oui, mais d’où vient \(\mathbf{N}\)? Est-ce que \(\mathbf{N}\) est un objet réel à explorer et découvrir dans un monde distinct de celui où nous vivons? Admettons-le pour un instant. Ainsi on découvre que \(\mathbf{N}\) est le siège d’opérations comme l’addition ou la multiplication, et que certaines parties de \(\mathbf{N}\) méritent une exploration spécifique, je pense à l’ensemble des nombres premiers et des merveilleuses découvertes et conjectures qui les concernent. Spontanément, les mathématiciens qui travaillent dans un domaine qu’ils connaissent bien sont dans cet état d’esprit, que le domaine n’est pas ce qu’après d’autres ils construisent, mais ce qu’ils explorent. Curieusement, cette attitude s’appelle le réalisme, alors qu’elle rompt avec la réalité ambiante, notre réalité de tous les jours. Mais c’est de considérer comme réels les objets de leurs études. Le monde des objets mathématiques apparaît comme un monde extérieur à l’humanité. Un très célèbre philosophe grec de l’antiquité, Platon, avait pour cela une image. Il voyait l’existence de l’humanité se dérouler dans une caverne. Les hommes y voyaient défiler des ombres qu’ils prenaient pour la réalité. Mais pour Platon la réalité se situait en dehors de la caverne, et seuls les mathématiciens et les philosophes y avaient accès. Spontanément, les mathématiciens sont platoniciens.
Mais on peut voir au contraire les abstractions mathématiques, à commencer par celle des nombres entiers, comme le résultat d’une lente élaboration à partir des connaissances et des pratiques des sociétés humaines.
Ainsi \(\mathbf{N}\) ne serait pas donné, mais construit au cours de l’histoire. Nous sommes moins doués que certains animaux pour reconnaître le plus et le moins, s’il y a plus d’œufs ici où là. Mais nous savons compter, et cela compense nos insuffisances, et va bien au-delà. Nous savons ajouter un, et découvrir en ajoutant un qu’il n’y a pas de nombre plus grand que tous les autres, c’est une première vision de l’infini.
On peut théoriser cette construction, et c’est la première axiomatique au sens moderne qui soit apparue en mathématiques. Dans cette optique, qui est la mienne, les objets mathématiques sont des constructions. Ce sont des constructions bien solides au point qu’on peut les croire éternelles et existant de toute éternité, mais elles sont sans cesse reprises et rebâties. Euclide est plus solide que le Parthénon, mais notre regard sur Euclide change au cours du temps, et les nombres entiers d’Euclide, et en particulier les nombres premiers d’Euclide, ont aujourd’hui un contenu bien plus riche que de son temps. La logique mathématique, qui date pour nous d’Aristote, est complètement renouvelée par l’informatique. L’image des mathématiques comme une merveilleuse construction humaine ne me paraît pas diminuer leur importance et leur valeur, au contraire.
Je vais passer aux figures géométriques, et je commence par la sphère. Suivant l’usage mathématique actuel, la sphère sera pour moi une surface et non un volume. Un ballon, une bulle de savon, le bord d’une boule de billard, sont des images familières de sphères. Et tout le monde connaît la définition d’une sphère: c’est l’ensemble des points de l’espace qui se trouvent à une distance donnée d’un point fixe, qu’on appelle le centre de la sphère. Réfléchissons un peu. On sait reconnaître une sphère en la voyant, en la tâtant, en la faisant rouler, en jouant avec. Mais qui a jamais vu le centre d’une sphère? La sphère définie à partir de son centre est une pure abstraction mathématique. C’est une merveilleuse abstraction: elle est simple et facile à comprendre, et c’est le bon point de départ pour développer la théorie de la sphère et mettre en évidence des propriétés caractéristiques en termes de distances, d’angles ou de courbure. Par exemple, de tout point de la sphère on voit un diamètre sous un angle droit, et c’est une propriété caractéristique: on peut définir la sphère comme l’ensemble des points d’où l’on voit un segment donné sous un angle droit. On pourrait prendre cela comme définition et procéder au développement de la théorie à partir de là, mais ce serait moins simple et moins naturel.
Il y a une intéressante discussion sur la sphère, le cercle et le plan entre un professeur et un élève dans la première leçon de géométrie donnée à l’École normale de l’an III, en 1794, et nous la connaissons parce que les cours et les discussions qui suivaient étaient pris en sténographie. Je vais vous en dire un mot. Le professeur est Gaspard Monge, un des grands mathématiciens de l’époque, et l’élève est Joseph Fourier, qui allait être un grand mathématicien de la génération suivante.
Ils s’appellent entre eux citoyen Monge et citoyen Fourier. Le citoyen Fourier vouvoie le citoyen Monge et celui-ci répond en tutoyant Fourier. Fourier présente une objection aux définitions données par Monge. Il est d’accord avec la définition de la sphère que j’ai donnée, à partir du centre et du rayon. Mais il critique la définition du cercle, que Monge a défini de la même façon mais comme une figure plane. Or Monge n’a pas défini le plan, et c’est ce que lui reproche Fourier en lui proposant une définition: un plan est l’ensemble des points qui se trouvent à égale distance de deux points donnés.
Monge apprécie l’ingéniosité de la remarque de Fourier, mais il estime qu’elle n’a pas sa place au début de son cours de géométrie. Il montre qu’on pourrait donner d’autres définitions de la sphère, comme je viens de le faire, et voici ce qu’il dit à ce propos:
«Il est vrai que, pour bien définir un certain ensemble d’objets, il faut exposer une propriété qui convienne à tous les objets du genre, et qui ne convienne qu’à eux seuls; mais cela ne suffit pas; il faut encore, parmi toutes ces propriétés, choisir celle qui est la plus simple et la plus facile à concevoir.
«Il faut enfin que la propriété qui sert de base à la définition soit féconde et conduise de la manière la plus directe aux autres propriétés plus compliquées qu’il est important ou de découvrir ou d’enseigner.»
Simplicité et fécondité, Monge nous donne les maîtres mots d’une bonne définition.
Avant de quitter la sphère, je reviens à Platon. Lorsqu’il parle des polyèdres réguliers, comme le cube, il dit de la sphère que c’est la figure la plus semblable à elle-même. Cela a interpellé certains traducteurs, parce qu’on a l’impression que toutes les figures sont semblables à elles-mêmes. Mais l’expression utilisée par Platon a un sens profond. Les polyèdres réguliers ont des symétries, disons, des rotations autour de leur centre qui les ramènent sur eux-mêmes, et ces rotations forment un groupe. Ce groupe est différent pour le cube et chacun des autres polyèdres réguliers. Le plus riche est celui du dodécaèdre qui a douze faces. Pour la sphère, toutes les rotations la ramènent sur elle-même, elle a le maximum de symétries, c’est bien la figure la plus semblable à elle même.
Un mot encore sur les polyèdres réguliers de Platon. Il y en a cinq, et les éléments fondamentaux de la chimie de Platon sont le feu, l’air, l’eau et la terre. Le feu est représenté par le tétraèdre, qui a quatre faces, l’air par l’octaèdre qui en a huit, l’eau par l’icosaèdre qui en a vingt, et toutes ces faces sont des triangles équilatéraux; reste la terre qui est représentée par le cube qui a six faces, des faces carrées et non triangulaires.

Patron d’un cube et cube
La chimie de Platon est la transformation de ces polyèdres les uns dans les autres. Oui, mais il reste un polyèdre qui ne représente rien, c’est le dodécaèdre. Au contraire, Platon lui donne un rôle supérieur ; c’est lui qui a servi de modèle à l’Univers. L’interprétation est claire : l’univers est sphérique, et le dodécaèdre est un bon modèle pour la sphère.
Comment voit-on que c’est un bon modèle ? Tout simplement en regardant un ballon de football tel qu’on en fabriquait dans mon enfance : douze pièces pentagonales, cousues, et gonflées à l’intérieur.

Ballon de football fait de pièces pentagonales
Et c’est bien ainsi que, selon Platon, Socrate décrit la Terre, juste avant sa mort. D’abord il explique qu’elle est sphérique. Puis, voici la façon dont elle apparaîtrait, vue du ciel :
« pour ce qui est de l’aspect qu’offrirait cette terre, si on la regardait d’en haut, ce serait à peu près celui d’un ballon bigarré, dans le genre des balles à douze pièces. »
À Athènes à cette époque, les artisans du cuir devaient fabriquer des ballons tout à fait semblables à nos ballons de football. Et avant de devenir des objets mathématiques, les dodécaèdres devaient être bien familiers aux enfants jouant avec ces ballons.
Je quitte Platon, mais pas encore les polyèdres et la sphère. On peut construire la sphère à l’aide de douze pièces pentagonales, c’est ce que nous venons de voir. Mais si, au lieu de douze pentagones, on utilise douze pentagones et vingt hexagones, on obtient une sphère plus proche encore de sa définition mathématique. C’est ce qu’a fait l’architecte Fuller en construisant un immense dôme à l’exposition universelle de Montréal en 1966, et depuis on appelle fullerène une pareille construction. Or on a découvert dans le cosmos, puis construit en laboratoire, des molécules de carbone ayant la forme d’un fullerène. Ces molécules sont formées de soixante noyaux de carbone occupant les sommets d’un fullerène, et elles sont de grand intérêt en chimie. Ainsi la chimie moderne rejoint les visions fantastiques de Platon sur la constitution de l’univers.

Ballon de football fait de pièces pentagonales et hexagonales
À l’École normale de l’an III et en réponse à l’élève Joseph Fourier, Gaspard Monge a insisté sur deux exigences pour avoir une bonne définition : elle doit être simple, facile à énoncer, et efficace, elle doit être un bon point de départ pour établir la théorie.
Et en effet, dans un cours de mathématiques, on commence par les définitions pour développer la théorie. La définition est le point de départ. Mais, historiquement, c’est un aboutissement. Selon moi, les notions mathématiques ne viennent pas d’un monde où il s’agirait de les découvrir, mais d’un effort pour rendre simples, généraux et intelligibles les résultats accumulés par des générations. Mon exemple favori est une phrase de trois mots qui exprime un résultat profond et subtil. Ce résultat avait été obtenu au début du 20e siècle par des mathématiciens qui avaient besoin pour l’énoncer d’un long discours. Quelques années plus tard, on a défini deux notions, qui s’appellent «\(L^2\)» et «complet».
Certains d’entre vous les rencontreront plus tard, mais il n’est pas nécessaire de les comprendre pour apprécier ce qu’est devenu le long discours. Il se réduit aux trois mots:
\(L^2\) est complet.
Toute la difficulté et la subtilité de la proposition sont passées dans les définitions. Avec de bonnes définitions, on a de bons énoncés.
Mais la simplicité des définitions et des énoncés est trompeuse. Elle résulte d’un travail de distillation, ou de sublimation, de tout ce qu’ont apporté les mathématiciens, et aussi bien d’autres, au cours des siècles. Aussi il faut prendre les définitions comme des élixirs de pensée, et prendre le temps de les assimiler en découvrant leurs conséquences dans les mathématiques qu’elles entraînent. Historiquement, c’est une partie de ces conséquences qui a engendré les points de départ des théories. Dans l’enseignement, on inverse l’ordre historique, c’est ce que les didacticiens appellent la {transposition didactique}. Si on reste à la définition, la richesse de la notion est cachée.
C’est le moment de démontrer un théorème: dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. Voici comment Clairaut l’enseignait à la marquise du Châtelet.
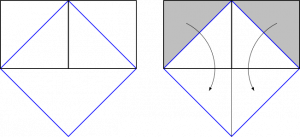
Cas particulier du théorème de Pythagore
On part de deux carrés égaux et adjacents, on trace deux diagonales faisant un angle droit, on les complète pour former un carré ; la surface de ce carré est la somme des surfaces des deux carrés de départ. C’est la démonstration du théorème de Pythagore dans le cas d’un triangle rectangle isocèle, et elle était classique au temps de Platon. La suite s’exprime mieux par des figures que par des mots, mais j’essaye ici d’en donner l’idée.
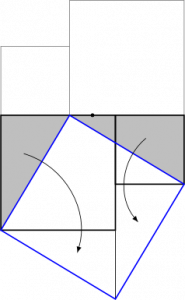
Preuve du théorème de Pythagore
Au lieu de deux carrés adjacents et égaux, ou les prend inégaux, avec les deux côtés horizontaux supérieurs en prolongement l’un de l’autre ; on prend leurs symétriques par rapport au centre du segment qui réunit ces deux côtés ; le symétrique du grand côté et le côté extérieur du petit carré forment un angle droit, ce sont les côtés du triangle à considérer ; en le faisant tourner d’un angle droit autour du sommet le plus bas de son hypoténuse on obtient un nouveau triangle par lequel on le remplace ; puis on opère de même avec le triangle rectangle construit sur le côté vertical extérieur du grand triangle et sur le symétrique déjà construit du petit côté ; après les remplacements la réunion des deux carrés de départ devient un carré construit sur l’hypoténuse ; ainsi le carré de l’hypoténuse est la somme des carrés des côtés de l’angle droit.
J’ai écrit cette démonstration avec des mots du langage mathématique courant, mais elle est plus compréhensible en faisant des figures et des constructions. Dans le langage mathématique il me paraît convenable d’inclure les figures.
Les figures sont comme des signes, ou des mots, et les constructions géométriques sont comme des phrases construites avec ces mots. Elles parlent à l’imagination, ce qui est essentiel en mathématiques. Si l’on n’y prend pas garde, elles provoquent aussi des erreurs, et la correction des erreurs fait aussi partie de la vie mathématique.
Les triangles rectangles constituent une mine de constructions intéressantes. À l’aide de leur hauteur on peut les décomposer en deux triangles qui leur sont semblables.
D’un triangle à une figure fractale
En répétant cette opération indéfiniment et en numérotant convenablement les triangles emboités qu’on obtient ainsi, on a finalement une courbe qui remplit tout le triangle rectangle. L’exploration de cette courbe est une bonne initiation à la géométrie fractale.
La courbe que je viens de décrire n’a de tangente en aucun point. C’est l’un des objets étranges que des mathématiciens ont construit à la fin du 19e siècle. Le premier a été une fonction continue qui n’avait de dérivée en aucun point. À l’époque ces constructions n’avaient pas bonne réputation. Charles Hermite, le plus grand mathématicien français de sa génération, disait, je cite :
« Je me détourne avec effroi et horreur de cette plaie lamentable que sont les fonctions continues qui n’ont point de dérivées. »
Il disait cela sérieusement, et les plus grands mathématiciens étaient de son avis. Et cependant, de pareils monstres commençaient à apparaître dans les mathématiques classiques. Plus clairement encore, ils sont apparus au début du 20e siècle avec les probabilités et les fonctions représentant des processus aléatoires. Le mouvement brownien donnait un exemple d’un phénomène physique, le mouvement désordonné de particules en suspension dans un liquide, qui était valablement représenté par une fonction continue nulle part dérivable, et par une courbe n’admettant de tangente en aucun point. Dès qu’on a étudié de façon systématique les processus aléatoires, de pareilles fonctions et courbes apparaissaient en nombre. Fallait-il, pour une courbe qui remplissait un carré, dire qu’elle était de dimension 2 et non de dimension 1 ? Oui, et la théorie a été faite de dimensions intermédiaires entre 1 et 2, et de façon générale de dimensions qui étaient des nombres réels positifs non nécessairement entiers. Elle date de 1919, elle est due à un grand mathématicien allemand, Felix Hausdorff, et elle joue un rôle fondamental dans ce qui allait devenir la géométrie fractale.
La géométrie fractale a complètement changé notre vue des objets mathématiques qu’on avait considérés comme des monstres, et des objets de la nature dont on n’avait pas entrepris l’étude mathématique. Elle est due à Benoît Mandelbrot, et date des années 1960. Benoît Mandelbrot était né en Pologne et il est mort aux États-Unis. Mais sa formation a été faite en France, il a été et est resté français, et j’insisterai sur l’importance du français comme langue dans les mathématiques qu’il a créées.
D’abord le terme de fractale. Il s’est introduit en plusieurs étapes. La première a été de parler de dimension fractale au lieu de dimension de Hausdorff, qu’on appelait alors couramment dimension fractionnaire. C’était une innovation modeste, et qui n’avait pas de quoi impressionner les mathématiciens. L’étape décisive a été la publication en 1975 du livre Les objets fractals. Le titre complet est Les objets fractals : formes, hasard et dimension. On voit tout de suite le rapport à la géométrie et aux probabilités. La traduction anglaise est venue en 1977, et le titre a été condensé sous la forme : Fractals : forms, chance, and dimension. Enfin est apparu en français le substantif féminin, « les fractales », avec comme compagnon l’adjectif fractal. Par exemple, Mandelbrot parle de « la géométrie fractale de la nature ».
Cette expression est parlante et rend bien compte d’observations éparses faites précédemment sur les côtes de Bretagne ou le cours de la Vistule. Les bizarreries mathématiques deviennent des pièces d’une véritable théorie.
L’apport de Benoît Mandelbrot aux mathématiques est aujourd’hui unanimement reconnu. Il tient à une vision d’ensemble qui lui était personnelle, et aussi, je veux y insister ici, à l’usage de la langue et à ses inventions verbales. Voici un exemple personnel que j’ai vécu. Avec Raphaël Salem, j’avais étudié des objets et des courbes étranges ; l’une de ces courbes représentait ce que nous appelions « la fonction de Lebesgue construite sur l’ensemble triadique de Cantor ». Bien sûr, cela ne dit rien à personne hors quelques mathématiciens. Mais Benoît Mandelbrot l’appelle « l’escalier du diable ». C’est une trouvaille verbale, qui attire tout de suite l’attention.
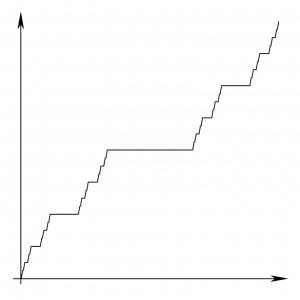
« L’escalier du diable »
De la même façon, « le flocon de neige » est bien plus attirant que « la courbe de Von Koch ». Je ne vais pas multiplier les exemples, il suffit de lire du Mandelbrot pour avoir conscience d’un véritable génie verbal.
Et son influence à cet égard s’est étendue a certains de ceux qui ont travaillé sur des objets mathématiques qu’il a créés. Le plus célèbre de ces objets est l’ensemble de Mandelbrot.
Pour ce que je vais en dire, il n’est pas nécessaire de connaître sa définition ; je la donne quand même, à l’intention des professeurs sinon des élèves. C’est une partie du plan des nombres complexes, constituée des points c tels que la fonction z2+c, appliquée successivement à 0 puis à l’image de 0 qui est c, puis à l’image de c et ainsi de suite indéfiniment, donne une suite de points qui reste à distance finie de 0. C’est un exercice qui vous est accessible de voir à quoi ressemble l’ensemble de ces points c situés sur la droite réelle. Mais l’ensemble des points c complexes a été et est toujours l’objet d’études difficiles. Mandelbrot en a donné des images qui se sont affinées au cours du temps, par informatique graphique. Celui qui a élucidé les propriétés essentielles, à savoir si l’ensemble était ou non d’un seul tenant, est un mathématicien français, Adrien Douady, qui était mon collègue à Orsay. Lui aussi avait un génie de la langue, et ses trouvailles sont restées seulement dans la mémoire de ses interlocuteurs. Au début, l’ensemble de Mandelbrot était figuré par une belle partie centrale, ornée de bosses, et de petits morceaux épars.


Pour Douady, ces morceaux épars étaient « les crottes de mouche de Mandelbrot ». Mais l’étude théorique, et d’ailleurs les dessins plus élaborés, montraient l’existence de fils reliant ces petits morceaux, qui cessaient donc d’être épars. Alors, pour Douady, ils sont devenus « des gouttes de rosée sur une toile d’araignée ».
Je conclus là-dessus. Les mathématiques sont une science en plein mouvement, qui forge sans cesse de nouveaux objets et un nouveau langage. Mais vous voyez, avec Douady, que pour en parler les mathématiciens utilisent la langue de tout le monde. Et vous voyez aussi que, pour reprendre la formule de Condorcet, les chiffres, les lignes, et toutes les mathématiques, parlent plus qu’on ne le croit à leur imagination, toujours en éveil.
Post-scriptum
Ce texte appartient au dossier thématique “Maths et langage”.



Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.