Nombres premiers, encore et toujours

Les nombres premiers, c’est comme Antigone, Œdipe, ou les jeux olympiques : ils intéressaient déjà Euclide, Sophocle et Pindare, et ils sont toujours au cœur de l’actualité (que d’histoires ! voir par exemple ⁷Article de Pierre Colmez à IdM : Histoires de nombres premiers.). Ainsi, après une quasi infinité de livres qui leurs sont consacrés, un mathématicien de la Côte Est des Etats-Unis en a publié tout récemment un nouveau, dans l’idée de le faire lire à ses enfants ⁸Voir ici les références précises pour « You can count on monsters » et là pour d’autres livres du même auteur. Merci à Richard Schwartz qui m’a généreusement fourni les fichiers des dessins reproduits dans ce billet..

Le livre de Richard Schwartz s’intitule « You can count on monsters », c’est-à-dire à peu près « Vous pouvez compter sur les monstres » (au sens où on compte sur ses doigts). Les quelques phrases qu’il contient sont en anglais, mais la majorité des pages sont strictement sans texte, avec quelques chiffres et de très jolis dessins. A chaque nombre de \(1\) à \(100\) correspond une page double. A gauche le nombre, accompagné d’un nombre égal de ronds de couleurs vives, et un diagramme indiquant s’il y a lieu la factorisation en nombres premiers ; à titre d’exemple, la page gauche pour \(35=5×7\).

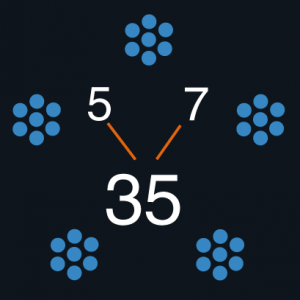
« S’il y a lieu », précisément si le nombre n’est pas premier (ni le nombre \(1\)), puisque par définition un nombre premier ne se factorise pas. A droite un dessin imaginé par l’auteur pour incarner le nombre. Ce qu’il appelle un monstre, c’est un dessin correspondant à un nombre premier, par exemple à \(3\) :

ou à \(31\)

et en fait à chacun des vingt-cinq nombres premiers inférieurs à 100. Pour un nombre composé, par exemple 14=2×7, le dessin de droite représente le monstre de 7 (où les enfants de sept à septant-sept ans s’amuseront peut-être à compter les 7 côtés de la tête, ou les 7 cheveux, cinq courts et deux longs, ou les 7 dents, ….) en train d’avaler le monstre de 2 (avec ses deux énormes yeux).

Le livre se termine par l’explication d’une méthode très classique pour reconnaître qu’un nombre \(n\) est premier : on suppose (c’est un argument qui fonctionne par étapes) qu’on a déjà dressé la liste des nombres premiers inférieurs à la racine carrée de \(n\), et il suffit de vérifier que \(n\) n’est divisible par aucun d’entre eux. Par exemple \(97\) est un nombre premier, car il est inférieur au carré de \(11\) et n’est divisible par aucun des nombres premiers \(2, 3, 5, 7\). C’est la méthode dite du crible d’Eratosthène ⁹Voir par exemple ici., illustrée par Schwartz avec de jolies couleurs.

Mais on peut parfois procéder autrement. Voici un petit truc, une astuce ¹⁰ Merci à Jean-Pierre Serre pour m’avoir une fois raconté cela, entre le dessert et le café. de John Tate ¹¹ Lauréat 2010 du prix Abel, « pour l’étendue et le caractère durable de son influence sur la théorie des nombres » ; voir la citation., pour montrer que les quatre nombres de la suite remarquable \(101, 103, 107, 109\) sont tous premiers. ¹² Il s’agit donc de quadruplés, autrement dit d’une suite de quatre nombres premiers de la forme \((n-4, n-2, n+2, n+4)\). Il y a d’autres telles suite, par exemple \((5, 7, 11, 13)\),\((11, 13, 17, 19)\), \((191, 193, 197, 199)\), et \((1871, 1873, 1877, 1879)\).
On peut conjecturer qu’il y a une infinité de telles suites, par analogie avec la conjecture classique dite
des nombres premiers jumeaux, selon laquelle il existe une infinité de nombres premiers \(p\) tels que \(p+2\) soit également premier : tout le monde y croit, mais personne ne sait le démontrer. Voir wikipédia. Pour des données plus techniques, voir aussi l’une des entrées pertinentes dans l’encyclopédie des suites d’entiers ou une autre page de wikipédia (toutes deux en anglais).. Si on connait le tout début de la liste des nombres premiers, qui est \(2, 3, 5, 7, 11\), il suffit de montrer que chacun de ces quatre nombres a deux propriétés : d’une part, il est plus petit que \(11 \times 11 = 121\), de sorte que, s’il était composé, il serait nécessairement un multiple d’un des nombres \(2, 3, 5, 7\) ; d’autre part il est égal à \(3 \times 5 \times 7 = 105\) plus ou moins \(2\) ou \(2 \times 2 = 4\),de sorte qu’il ne peut pas être un multiple d’un des nombres \(2, 3, 5, 7\).

La méthode s’applique à d’autres nombres premiers : par exemple, pour les nombres premiers entre \(6\) et \(25\) :

\(7 = 2 \times 2 + 3\) (ou \(3 \times 3 – 2\)),

\(11 = 2 \times 2 \times 2 + 3\), ce qu’on écrit plus lisiblement \(11 = 2^3 + 3\),

\(13 = 2^2 + 3^2\) (ou \(2^4 – 3\)),

\(17 = 2^3 + 3^2\),

\(19 = 2^4 + 3\),

\(23 = 2^5 – 3^2\).

On peut dresser des listes analogues de nombres premiers entre \(26\) et \(49\), puis entre \(50\) et \(121\), entre \(122\) et \(169\), entre \(170\) et \(289\), etc.
Par exemple : le calcul \(277 = 2^2 \times 3 \times 5 \times 7 – 11 \times 13 < 17^2 = 289\)
montre que \(277\) est premier. Pour le lecteur tenté par l’exercice : bonne chance ! Pour les autres : un dernier tableau de Richard Schwartz qui récapitule les pages de droite.