
En novembre 2004, a été publié, je ne me souviens plus où, un rapport dont le titre était : Les savoirs fondamentaux au service de l’avenir scientifique et technique de la France. Il était signé par sept académiciens : Roger Balian, Jean-Michel Bismut, Alain Connes, Jean-Pierre Demailly, Laurent Lafforgue, Pierre Lelong et Jean-Pierre Serre. À ce titre, il fut ainsi surnommé le Rapport des 7 académiciens.
Je lis « Nous, mathématiciens, scientifiques, nous sentons extrêmement concernés par l’École et attachés à elle d’abord parce que sans elle nous ne serions rien de ce que nous sommes aujourd’hui. Le meilleur voeu que nous puissions formuler pour les jeunes générations est que leur soient offertes les mêmes chances que celles dont nous avons bénéficié. Pour la plupart d’entre nous, quand nous nous remémorons nos histoires personnelles ou familiales, nous n’avons pas besoin de remonter très loin pour trouver des générations dépourvues d’instruction mais dont les enfants ont pu découvrir grâce à l’école le monde épanouissant de la lecture, des livres et du savoir. »
Ce rapport de 28 pages, bibliographie comprise, comporte aussi des indications sur les programmes, indications qui pourraient être discutées, susciter un accord ou un désaccord, mais qui, dans tous les cas, ont leur intérêt. Ce qui me frappe dans ce rapport, c’est le paragraphe 6.3. intitulé : Dans quel état d’esprit faut-il enseigner ?
Je lis encore : L’état d’esprit de l’enseignement est presque plus important que le contenu lui-même – on pourrait dire qu’il est constitutif de ce contenu. Un des buts principaux des Mathématiques doit ainsi être l’apprentissage du raisonnement et de la rigueur.
Et plus loin : Un autre but de l’enseignement des Mathématiques, et en même temps l’un de ses principaux intérêts pour la formation de l’esprit, est d’apprendre aux élèves à ne rien admettre qu’ils n’aient pas vérifié par eux-mêmes. Puis : Un troisième but essentiel de l’enseignement des Mathématiques est de faire découvrir aux élèves la puissance de l’abstraction.
Ces trois indications, davantage développées dans le rapport, sont toujours pour moi source de réflexion. Surtout la première, sur laquelle je m’attarde depuis quelques années. J’ai été invité à l’approfondir davantage en vue des formations que j’allais donner pour des conseillers pédagogiques.
C’est le point essentiel de ce débat. Dans beaucoup d’échanges autour des programmes, nous, les professionnels des programmes, insistons énormément sur les contenus et rarement sur l’état d’esprit de l’enseignement. Ce questionnement amène aux deux autres titres de ce débat : Peut-on définir l’esprit mathématique ? Et au fait, quel est ce besoin de le définir ?
Les questions sont à mon avis toujours ouvertes. Chaque lecteur pourra y apporter ses réponses ou sa réflexion aujourd’hui et tout au long de sa vie professionnelle.
De mon côté, loin de vouloir fournir une réponse définitive ou de renfermer ce débat en quelques vérités, à la lumière des formations que j’ai données en direction de l’école primaire, je trouve intéressant que certains sujets aient énormément attiré la curiosité des formateurs que j’ai eus en face de moi.
Par exemple, la notion de nombre et les difficultés pour le définir. Le cheminement long et pas toujours connu de cette notion jusqu’à Bertrand Russel, Gottlob Frege ou Giuseppe Peano.
Une des difficultés lorsqu’on aborde la notion de nombre, consiste à croire que la propriété de commutativité va de soi… Et l’enseignement renforce cette croyance. Finalement, je me demande : combien d’opérations dans la vie courante jouissent de cette merveilleuse propriété ? Je me dis, car je le constate expérimentalement, que la vie est fondamentalement non commutative. Si je me le dis seul, dans mon bureau par exemple, ça va encore. La question, formulée devant un public même averti, désarçonne. La propriété que \(a + b = b+ a\) est tellement ancrée dans nos esprits que l’on n’ose plus en douter ; à tel point que nous finissons par penser ou nous dire que les opérations de la vie de tous les jours sont toujours commutatives. Comme tous les matins, je sors du lit puis je mets mes pantoufles, puis je mets mes lunettes, puis je descends les escaliers pour aller dans ma salle de bain, puis je prends d’abord ma douche, puis j’enfile mon peignoir…. Je vous laisse continuer la liste. C’est amusant !
La notion d’infini dénombrable et non dénombrable. Les paradoxes. Par exemple, le cardinal des nombres entiers est le même que celui des entiers pairs. L’idée que le tout est plus grand que la partie est alors mise en discussion lorsque ce tout n’est pas formé d’un nombre fini d’objets, mais d’une infinité !
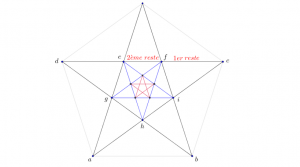
Puis, contrairement à ce que l’intuition pourrait faire croire, il arrive qu’il n’y ait pas de commune mesure pour deux grandeurs. Un exemple parmi d’autres : il n’y a pas de commune mesure entre le côté et la diagonale d’un pentagone régulier (cf. figure prise dans le livre de Nicolas Rouche Le sens de la mesure, éditions Didier Hatier).
En suivant N. Rouche et en appliquant l’algorithme d’Euclide (voir figure pentagone) au côté \(ab\) et à la diagonale \(dc\) puis en portant \(ab = ec\) sur \(dc\), on trouve que \(ab\) peut être reporté une fois et qu’il reste \(de = fc\). Or \(fc\) peut être reporté une fois dans \(ab = ec\) et il reste \(ef\). On remarque alors que les deux restes sont \(fc = gh\)et \(ef\). Le premier est la diagonale du pentagone \(efihg\), et le second est le côté de ce même pentagone. Les deux premiers pas de l’algorithme d’Euclide nous ont donc ramenés « à la case départ » : trouver une commune mesure entre le côté et la diagonale d’un pentagone régulier. L’algorithme se répète indéfiniment de façon similaire. Or, s’il y avait une commune mesure, il s’arrêterait. Finalement, il n’y a pas de commune mesure !
Cette démonstration demande bien évidemment certains préliminaires pour être suivie correctement. Ce qui est intéressant ici est qu’elle fait naître une interrogation : mais alors n’y aurait-il pas toujours de commune mesure pour deux grandeurs ?
Finalement, je tourne autour de la question : Peut-on définir l’esprit mathématique ?
Je continue à chercher, car cet esprit mathématique – nous l’avons vu avec quelques exemples – est vraiment particulier. Et s’il n’y en avait qu’un !…
Cette spécificité de l’esprit mathématique (je continue à utiliser le singulier) et sa recherche, là où plus ou moins celui-ci se cache, sont motivées par la deuxième question de ce débat : Et au fait, quel est ce besoin de le définir ?
Voilà quelques idées que je tenais à partager avec vous, chers lecteurs, mais aussi – ce qui est plus important – l’étonnement des formateurs, comme celui des enfants (d’école primaire et/ou de collège), quand on leur fait découvrir qu’au-delà d’une utilité pratique, les mathématiques nous réservent bien des surprises.





8h53
Voir les 4 commentaires