Pierre Gallais est un artiste qui puise son inspiration dans les maths. Nous nous sommes rencontrés il y a quelques années alors qu’il cherchait des informations sur les ellipsoïdes… Eh oui, depuis longtemps il est fasciné par les ellipses et les hyperboles… Il n’est pas le seul : on a déjà parlé d’ellipses dans Images des Mathématiques, ici, ici encore, là, là encore, et encore ici et on en reparlera encore.
Regardez par exemple ce que Pierre Gallais a réalisé dans un village de la Nièvre en 2000. Après la moisson, il s’agissait d’organiser les bottes de paille sur des ellipses en respectant la loi des aires de Kepler.
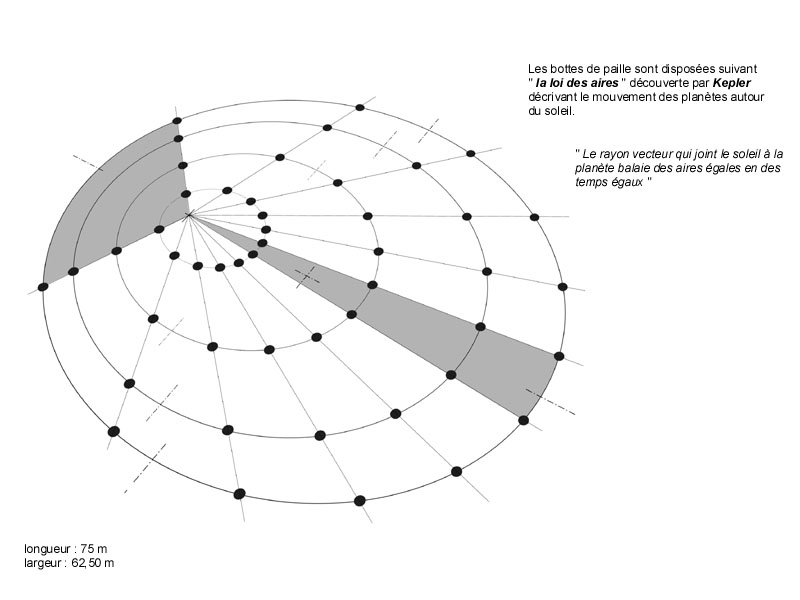
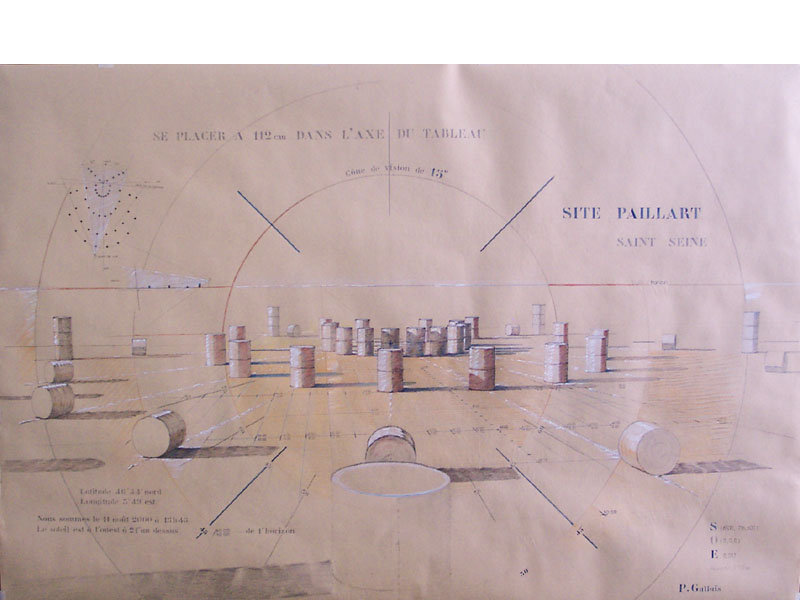
- Alors, après les ellipses, il fallait bien passer aux ellipsoïdes. Il s’agit de surfaces qui jouent un rôle crucial en mathématiques. Comme chacun sait, un ballon de rugby n’est pas rond mais il l’est quand même un peu… Si on le coupe en tranches par des plans perpendiculaires à son « grand axe », on obtient des rondelles circulaires.Voici par contre un ellipsoïde général.
.
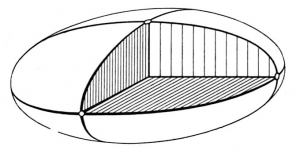
Ses trois axes sont de longueurs différentes. Allez-donc jouer au rugby avec un ballon de cette forme ! Cette petite figure est extraite du merveilleux livre de Hilbert et Cohn-Vossen « La géométrie et l’imagination » qui a probablement été à l’origine de plus d’une vocation de géomètre. 4Hilbert, Cohn-Vossen, La géométrie et l’imagination. La version allemande date de 1932. On peut consulter une partie de la traduction anglaise sur google books ou bien acheter ce beau livre, par exemple ici. Pour le rugby, deux des axes sont égaux et pour le football les troissont égaux et on a tout simplement une sphère. Si on coupe un ellipsoïde par un plan quelconque, la tranche est une ellipse5 J’entends d’ici mes collègues dire qu’il faudrait préciser que l’intersection peut être vide ou réduite à un point. Mais qui aurait l’idée de couper un objet par un plan qui ne le coupe pas, à part un mathématicien !. On rencontre finalement assez peu de « vrais ellipsoïdes » dans la nature, c’est-à-dire avec trois axes de longueurs différentes6Même si la forme de certains galets s’en approche : grand débat entre les géologues et les physiciens… .
Il était donc logique que Pierre Gallais s’intéresse aux ellipsoïdes. Il découpait des ellipses à la scie circulaire dans des planches de bois, il les collait les unes sur les autres, puis ponçait l’ensemble soigneusement. Les ellipsoïdes de Pierre sont assez grands ; certains ont un grand axe de près d’un mètre. Quand il est venu me rencontrer, il cherchait à tracer des courbes sur ses ellipsoïdes avec des bandes adhésives ; en déroulant le rouleau sur la surface sans faire de plis, le rouleau décrit une courbe que nous appelons une géodésique et que Pierre trouvait jolie… Il cherchait à comprendre ces géodésiques. J’ai eu le plaisir de lui montrer comment le mathématicien Jacobi, il y a 150 ans, avait complètement décrit la nature de ces courbes, mais ceci est une autre histoire.
Maintenant, Pierre Gallais connaît une autre méthode pour fabriquer les ellipsoïdes.
Si on coupe un ellipsoïde par un plan, on obtient une ellipse qui n’est en général pas un cercle bien sûr. Si on fait pivoter un plan autour de l’axe moyen, les découpes elliptiques vont se déformer au cours de la rotation. Regardez la figure suivante et essayez de vous convaincre que pour une inclinaison convenablement choisie d’un plan qui contient le moyen axe, la découpe est un cercle.
.
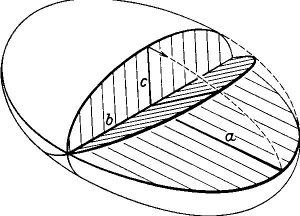
On peut donc réaliser des ellipsoïdes en empilant des tranches parfaitement circulaires ; c’est plus facile et le résultat est plus joli. Voici les ellipsoïdes de Pierre, exposés dans un lycée :
.
Voici une autre figure extraite du livre de Hilbert et Cohn-Vossen. Cette figure montre que l’ellipsoïde peut être obtenu en empilant des disques de deux façons, symétriques l’une de l’autre.
.
Dans ce même livre, on trouve un théorème incroyable. Supposons qu’on réalise les deux familles de cercles sur l’ellipsoïde en fil de fer de telle sorte que les points d’intersection permettent une rotation mais pas de glissement (j’avoue que n’étant pas très bricoleur, je ne saurais pas trop comment faire ça en pratique…). Alors l’ensemble de ces fils de fer avec toutes ces jointures est flexible : en appuyant légèrement sur cette structure, elle se déforme progressivement en prenant la forme d’autres ellipsoïdes, ayant d’autres axes ; les fils gardent leur forme circulaire. On peut même continuer la déformation jusqu’au moment où toute la structure a été aplatie dans un plan. Lecteurs de Images des Mathematiques : démontrez-le !
Voici l’ellipsoïde précédent (en carton) après déformation.
.
Revenons à Pierre !
En 2003, il fonde l’Institut de Mathologie (dont il est le seul membre) et envoie un petit journal, le Mathazine, par courrier électronique à ceux qui le souhaitent. Récemment, il a eu la bonne idée de réunir tout cela dans un beau livre, bien sûr publié « à compte d’auteur ».
Pour vous donner une idée du style et de la poésie de Pierre Gallais, voici l’une des pages de Mathazine :
Avant projet pour une
SEINTHÈSE
prothèse… fouthèse… seinthèse ?
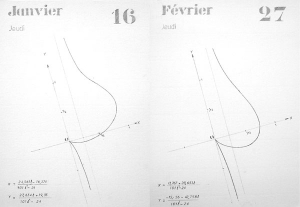
Il n’est pas aisé de commencer le récit d’une aventure qui s’étale sur déjà plusieurs décennies . Ci-dessus deux courbes (cubiques unicursales) dont les équations paramétriques apparaissent en bas à gauche…. une certaine émotion rencontrée en classe préparatoire. Ci-dessous une page arrachée à un livre de mathématique et une formulation qui provoqua sinon un grand émoi… un grand moment de poésie lorsque nous la rencontrâmes en potassant pendant les vacances le livre de math qui devait être étudié en classe de terminale. (Pour qui peut lire ce genre d’écriture nous conseillons de la lire à voix haute)… Expression nouvelle dans une écriture et une langue pour laquelle nous n’étions pas encore très assuré. Alors… nous nous raccrochons au plaisir des signes, de l’écriture, de la composition… une certaine forme de calligraphie ? Pendant de nombreuses années nous avons été beaucoup embarrassé par le terme « poésie ». Qu’est-ce ? Quelle définition et pire quel contenu ? Comment oser reconnaître et affirmer que nous avons ressenti de l’émoi ou de la poésie devant une telle expression…. ? sans s’exposer à se faire traiter de « pathologique » ou bien, pire encore pour un mathématicien en herbe… de « pas trop logique » !
Dans notre voisinage il n’y avait pas d’inconnues… le village était petit… mais une grande indéterminée « Mathdemoiselle » avec tout ce que cela travaille dans l’esprit d’un adolescent. La notion de limite… s’en approcher aussi près que l’on veut sans jamais l’atteindre… et parfois… au contact… il se peut que le résultat soit différent de ce à quoi on s’attendait. Le résultat bien que différent ne contredit pas le rêve… la limite n’est que « ce vers quoi on tend » *. Cette expression réussit à traduire en une manière « calculable » une situation qui atteint le niveau sensoriel et émotionnel. Quelle merveille pourrait-on oser dire ! Nous retrouverons une émotion similaire en lisant plus tard René THOM dans sa « Théorie des Catastrophes » que nous interpréterons à notre manière. Ces expressions « calculables » qui permettent de jeter des ponts (via l’interprétation) entre le qualitatif et le quantitatif ou réciproquement. Dans cette formulation est contenu tout ce qui pose le dilemme du « mathématicien vivant » : prouver… peut-on prouver l’émotion ou la poésie ?… Pas étonnant que cela ait (inconsciemment) frappé « l’adolescent-mathématicien-en-herbe ». Là se situe peut-être la bifurcation qui détermine le choix (l’orientation) entre une carrière de « mathématicien pur » et une « carrière d’artiste »… Discontinuité : La courbe étant discontinue, tant qu’on approche du point de discontinuité **, que ce soit par le chemin mathématique ou par le chemin artistique la limite (l’espoir) est la (le) même… si on se place au point de discontinuité… tout fout-le-camp. Tant qu’on n’a pas pris conscience de la discontinuité on n’est pas bien dans ses baskets… on a tendance à s’accuser. Et puis il y a la situation (bâtarde ?) du « mathématicien-artiste » qui considère la courbe définie et continue : la branche mathématique de la courbe rencontre la branche artistique en un point réel*** : « l’artmathan » (à méditer… ou décliner). Point bâtard tout autant pour le mathématicien-pur que pour l’artiste-pur. À suivre…
Notes :
* Par nature nous sommes plus habitués ou enclins à considérer les choses comme définies continues ( au quel cas la limite coïncide avec la valeur ) mais de fait très souvent dans la vie il y a discontinuité (la valeur vers laquelle on tend diffère de la valeur que la chose prend quand on l’atteint (si on arrive à l’atteindre)) ; tant que l’on s’approche on peut conserver cet espoir de la limite… (c’est le rêve qui nous fait vivre… la réalité ?…!…)
** A supposer encore que la courbe ait une limite en ce point (qu’on peut appeler le rêve, l’espoir, le fantasme…). Que la fonction puisse même ne pas être définie en ce point (c’est à dire qu’il n’y a pas de sens à parler d’un art mathématique) n’a aucune incidence… pourvu qu’on ait une limite (de quoi rêver, espérer, fantasmer)
*** Il faudrait plutôt dire point « effectif » car nous sommes plutôt dans un espace où les nombres sont des « complexes » avec leur « composante réelle » et leur « composante imaginaire pure ». Nous nous devons de nous excuser auprès du public qui ne pourrait pas tout comprendre, il est impossible d’éviter un certain vocabulaire qui relève spécifiquement de la langue mathématique… et crée des ambiguïtés (mais ça a du bon…) avec la langue courante.
Pour plus d’informations sur le travail de Pierre Gallais, consultez son site.
Vous pouvez en particulier lui écrire pour lui commander son bouquin…
ÉCRIT PAR
Étienne Ghys
Directeur de recherche CNRS émérite, Secrétaire perpétuel de l'Académie des sciences - École Normale Supérieure de Lyon
