Le « débat du 18 octobre » a donné lieu à quelques commentaires ….
Le triangle est une figure élémentaire de la géométrie plane, et sans doute celle qui recèle le plus de propriétés géométriques, à la fois simples et souvent un peu surprenantes. Par exemple la propriété qui suit, dont une des applications pratiques est l’estimation de la distance totale entre trois magasins et un dépôt de marchandises qui les approvisionne, situé à l’intérieur du triangle dont ils sont les sommets. Voici son :
Énoncé
Soit \(ABC\) un triangle de périmètre \(p=AB+BC+AC\). Alors, pour tout point \(M\) intérieur à \(ABC\),
on a} : \({p\over 2}\leq MA+MB+MC\leq p-\inf (AB,BC,AC)\).
Comme je l’avais dit dans mon billet, la première inégalité \(MA+MB+MC\geq {p\over 2}\) est presque immédiate à établir. J’avais aussi évoqué les difficultés que rencontrent les étudiants (de Master enseignement !) à démontrer que, pour le même point \(M\),
on a en plus \(MA+MB+MC\leq p\). Dans son commentaire, Bruno Langlois m’a indiqué qu’en fait on peut « raffiner » cette inégalité en :
\[MA+MB+MC\leq p-\inf \{ AB,BC, AC\} .\tag{1}\]
Je ne connaissais cette propriété que pour le point de Torricelli du triangle. Je n’ai pas eu le temps de réfléchir dessus tout de suite après (ce qui explique ma réponse tardive au commentaire). Quand j’ai pu le faire, mon premier réflexe a été de chercher si cette inégalité se trouve quelque part dans un livre et aussi en « googlant » sur le net. Mais je n’ai rien trouvé. Il ne me restait plus qu’à me mettre dessus ! Cela m’a pris un peu de temps mais j’ai pu arriver à une preuve purement géométrique et assez élémentaire dans le sens où elle ne fait appel qu’à des notions dont peut disposer un élève de Troisième. Je la livre telle quelle aux lecteurs d’IdM pour deux raisons :
1. La mettre à la disposition de ceux que ce type de problèmes intéresse : les collègues du primaire, du secondaire, et quelques-uns du supérieur.
2. J’aime bien ma preuve mais je me dis qu’il doit y avoir sûrement une encore plus simple, à côté de laquelle je suis passé et qu’un lecteur peut livrer. Et il y en a une, et j’espère qu’il y en aura d’autres !
Voici ma :
Preuve
Elle n’est pas si immédiate mais elle n’est pas compliquée non plus : elle utilise les deux remarques (simples) qui suivent.
Remarque 1. Soient \(\alpha \) et \(\beta \) deux angles d’un triangle opposés respectivement aux côtés \(a\) et \(b\). Alors \(\alpha \leq \beta \) si, et seulement si, \(a\leq b\).
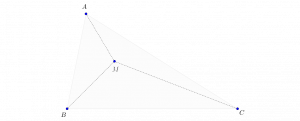
Remarque 2. Soient \(XYZT\) un parallélogramme d’angle \(\widehat{TXY}\) aigu. Alors, pour tout point \(M\) intérieur
à \(XYZT\), on a \(XM\leq XZ\).
La première assertion est bien connue. De la deuxième le lecteur peut s’en convaincre facilement : il suffit juste qu’il jette un petit regard géométrique sur la figure ci-dessous.
\(\bullet \) On suppose que \(BC\) est le plus petit côté du triangle \(ABC\). L’inégalité qu’on doit établir s’écrit alors :
\[MA+MB+MC\leq AB+AC.\tag{2}\]
\(\bullet \) On a aussi des inégalités entre les angles (user de la Remarque 1)) :
\[\widehat{BAC}\leq \widehat{ABC}\hskip0.5cm \hbox{et}\hskip0.5cm \widehat{BAC}\leq \widehat{ACB}\]
qui forcent l’angle \(\widehat{BAC}\) à être aigu (en fait sa mesure est inférieure ou égale à \({\pi \over 3}\)).
\(\bullet \) Soient \(K\in [AB]\) et \(L\in [AC]\) tels que \(BK=BM\) et \(CL=CM\). Alors l’inégalité \(MA+MB+MC\leq AB+AC\) est équivalente à :
\[AM\leq AK+AL\tag{3}\]
et c’est ce qu’on va établir.
\(\bullet \) Soit \(N\) l’unique point tel que le quadrilatère \(AKNL\) soit un parallélogramme. La parallèle à \((AB)\) passant par \(M\) coupe \([AC]\) en \(X\) et \([BC]\) en \(Y\). On a :
\[\widehat{CXM}= \widehat{CAB}\leq \widehat{CBA}=\widehat{CYX}\leq \widehat{CYX}+\widehat{YCM}=\widehat{CMX}.\]
Donc \(MC\leq CX\) (dans le triangle \(CXM\) le côté \(MC\) est opposé à l’angle \(\widehat{CXM}\) qui est plus petit que l’angle \(\widehat{CMX}\) opposé au côté \(CX\)). Mais \(MC=CL\) ; par suite \(CL\leq CX\). On en déduit que le point \(M\) est dans la bande délimitée par les deux droites parallèles \((AK)\) et \((LN)\).
De la même manière, en utilisant cette fois-ci l’inégalité \(\widehat{BAC}\leq \widehat{ACB}\), on montre que \(M\) est dans la bande délimitée par les deux droites parallèles \((AL)\) et \((KN)\). Le point \(M\) est donc à l’intérieur du
parallélogramme \(AKNL\) dont \(\widehat{KAL}\) est un angle aigu. D’où, en vertu de la Remarque 2 et de l’inégalité du triangle (appliquée au triplet \((A,K,N)\)) :
\[AM\leq AN\leq AK+KN=AK+AL\]
qui est l’inégalité (3).
J’ai fait savoir à Bruno Langlois que j’ai une preuve. Il m’a alors indiqué la référence d’une autre (peut-être « plus élémentaire ») donnée par J.N. Wisschsers en 1902 dans le périodique De Vriend der Wiskunde et reprise par Marie Berrondo-Agrell dans son livre Géométriquement vôtre paru en 1994.
La voici :
Elle utilise aussi de manière fondamentale (et un peu camouflée) une :
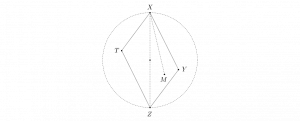
Remarque 3. Soit \(AKL\) un triangle tel que \(AK\leq AL\). Alors, pour tout point \(M\) du côté \(KL\), on a \(AM\leq AL\).
La preuve de cette assertion se voit sur le dessin ci-dessus. Soit \(H\) le pied de la hauteur issue de \(A\) ; alors \(KH\leq HL\) (simple application du théorème de Pythagore). Cette inégalité nous permet de montrer que \(AM\leq AL\) pour tout point \(M\) sur \(KL\). En effet, si \(M\) est sur \(HL\), l’inégalité \(AM\leq AL\) est immédiate ; si \(M\) est sur \(KH\), son symétrique \(M’\) par rapport à \(H\) est sur \(HL\), d’où \(AM=AM’\leq AL\).
\(\bullet \) On suppose \(BC\leq AB\leq AC\). Démontrer l’inégalité (1) revient donc à démontrer l’inégalité :
\[MA+MB+MC\leq AB+AC.\tag{2′}\]
C’est ce qu’on va faire. On mènera la preuve en regardant le dessin qui suit.
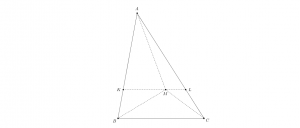
\(\bullet \) Par le point \(M\) on mène la parallèle au côté \(BC\) ; elle coupe \(AB\) en \(K\) et \(AC\) en \(L\). Comme les triangles \(ABC\) et \(AKL\) sont semblables,
on a \(KL\leq AK\leq AL\) (puisque par hypothèse \(BC\leq AB\leq AC\)). On a aussi, par la Remarque 3, \(MA\leq AL\). D’autre part, l’inégalité du triangle appliquée à chacun des triplets \((M,B,K)\) et \((M,C,K)\) donne les deux inégalités
\[MB\leq MK+KB \hskip0.5cm \hbox{et} \hskip0.5cm MC\leq ML+LC.\]
En définitive on a :
\[\cases{KL \leq AK \cr MA \leq AL \cr MB \leq MK+KB \cr MC \leq ML+LC}\]
\(\bullet \) En additionnant membre à membre les quatre inégalités, on obtient :
\[\eqalign{(MA+MB+MC)+KL&\leq AL+ (MK+KB)+(ML+LC)+AK\cr &=(AL+LC)+(MK+ML)+(AK+KB)\cr &=AC+KL+AB.}\]
D’où \(MA+MB+MC\leq AB+AC\) qui est l’inégalité cherchée.
Quelques collègues (parmi eux Bruno Langlois) proposent (chacun de son côté) de considérer la fonction convexe
\(f(M)=MA+MB+MC\) et lui appliquer le théorème qui dit qu'{une fonction réelle convexe, définie sur un convexe atteint son maximum en un point extrémal} (qui serait ici le sommet \(A\)). C’était aussi une idée
que j’avais tout au début mais je l’ai abandonnée parce qu’elle est nettement au-dessus du niveau des collégiens.
Post-scriptum
Je remercie Bruno Langlois pour son commentaire (qui a été très utile) et de m’avoir communiqué la référence de la preuve de J.N. Wisschsers.
ÉCRIT PAR
Aziz El Kacimi
Professeur émérite - Université Polytechnique Hauts-de-France
