Les processus de croissance sont une catégorie particulière de procédés aléatoires de construction de formes géométriques. Je ne vais parler ici que de certains cas particuliers, introduits je crois par Daniel Richardson en 1973.
Présentation
L’idée est la suivante : on se place sur un damier infini, on choisit un nombre \(p\) entre \(0\) et \(1\) et on se munit d’une pièce biaisée, qui donne pile avec probabilité \(p\). On commence avec une case du damier noire et toutes les autres blanches. Pour chacune des quatre cases adjacentes à la case noire, on fait un jet de notre pièce ; si le résultat est pile, on colorie la case en noir.
On continue ainsi, en jetant à chaque étape la pièce pour chaque case blanche adjacente à (au moins) une case noire et en coloriant en noir celles pour lesquelles on obtient pile.
Au fur et à mesure qu’on continue, on colorie peu à peu tout le damier. On se pose la question amusante suivante : quelle forme prend la partie coloriée en noir ? Ce qui nous intéresse ici n’est pas la taille, on peut par exemple imaginer qu’on regarde vers le damier depuis un point de plus en plus éloigné, de façon à toujours voir la partie noire à peu près de la même taille.
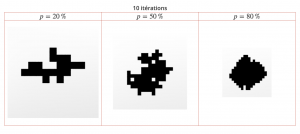
Voici quelques images qu’on obtient ainsi.
Et enfin, pour \(p = 50 %\), ce qu’on peut obtenir avec 500 itérations.
.
Un résultat surprenant et une question ouverte
Le résultat que démontre Richardson peut paraître surprenant : la forme construite par ce processus aléatoire converge (presque sûrement) vers une « forme limite » qui dépend de \(p\), mais qui est déterministe et pas aléatoire. C’est-à-dire que les lancers de pièces finissent par compter assez peu, et que si on recommence plusieurs fois le processus avec une même valeur de \(p\) et un grand nombre d’étapes, les formes obtenues se ressembleront très probablement beaucoup (de loin).
On ne sait pas, à l’heure actuelle, décrire la forme limite en fonction de \(p\). Quelques informations ont été obtenues quand \(p\) est proche de \(1\), mais on ne sait à ma connaissance presque rien sur la forme limite quand \(p\) tend vers \(0\). Richardson avait conjecturé qu’elle tendait vers un disque, mais des simulations numériques semblent indiquer que la vitesse de croissance est un peu plus faible dans la direction des diagonales que dans les directions horizontale et verticale.
Plein de variantes
On peut considérer de nombreuses variantes de ce problème, voir par exemple les sites web de Régine Marchand et Olivier Garet. Par exemple, on peut simplement pratiquer le processus en dimension plus grande (essentiellement, tout ce que j’ai dit plus haut reste vrai) ce qui donne par exemple l’image suivante(\(p=20%\), \(60\) itérations) :
ÉCRIT PAR
Benoît Kloeckner
Chercheur associé - Laboratoire d’Analyse et de Mathématiques Appliquées - Université Paris-Est Créteil Val de Marne
23h19
Merci pour cet article que j’ai trouvé très intéressant, j’apprécie particulièrement prendre connaissance de questions ouvertes, qui nous montre que tout n’est pas fait.
J’avais également une question par rapport à votre article : vous dites que l’on affecte la couleur noir ou blanc aux cases adjacentes à une autre selon le résultat d’un tir au hasard, mais retire-t-on au sort la couleur d’une case déjà « testée » ?
Merci de votre réponse
14h25
Dans la variante que j’ai présenté, une case noire le reste pour toute la suite du processus, on ne fait plus de tirage la concernant.
En fait, on peut étudier des processus plus généraux (et c’est d’ailleurs ce que fait Richardson) où, par exemple, à chaque étape chaque case noire a une petite probabilité de redevenir blanche. Alors si mes souvenirs sont bons, suivant les paramètres choisis, soit le damier devient tout blanc presque sûrement, soit ce que j’ai dit dans le cas simple reste vrai.