Alessio Figalli est un mathématicien italien qui vient d’obtenir la médaille Fields, à 34 ans, lors du congrès international des mathématiciens qui a eu lieu en août dernier à Rio de Janeiro. Alessio a des liens très forts avec l’école française de mathématiques : il a préparé son doctorat sous la codirection de Luigi Ambrosio (Pise) et Cédric Villani (Lyon), et a travaillé deux ans comme chargé de recherches à Nice et Polytechnique.
Le fait qu’il ait accepté de donner un exposé de recherche au séminaire du laboratoire Jacques-Louis Lions (Paris) peu de temps après l’obtention de sa médaille donne une idée de son attachement aux mathématiques françaises. Voici un court texte expliquant le contenu de son exposé, qui a eu lieu le 4 octobre.
Quelle est la forme d’un morceau de glace en train de fondre ? J’ai eu le plaisir de pouvoir écouter Alessio Figalli nous parler de cette question lors d’un exposé intitulé « Régularité des interfaces dans les transitions de phase modélisées par des problèmes avec obstacle » (pas de panique, moi non plus au début de l’exposé je ne comprenais pas le titre !).
Alessio a commencé par nous expliquer comment traduire ce problème en termes mathématiques, « modéliser ». Cette modélisation aboutit sur ce qui est appelé problème de Stefan, du nom du physicien slovène Josef Stefan qui l’a étudié aux alentours de 1890. Comme souvent en sciences, le problème ne doit pas son nom à son inventeur, puisqu’il avait déjà été étudié 60 ans plus tôt par les français Gabriel Lamé et Émile Clapeyron.
Cette modélisation est assez simple : on considère un bout de glace plongé dans un bac d’eau 6C’est à mon avis le principal défaut du modèle : la glace y est supposée entourée d’eau, alors que dans la vraie vie, elle flotte !. Toute la glace est à une température de 0°C, et l’eau qui l’entoure est à une température positive. Reste à dire comment la glace fond : en tout point de l’interface glace-eau, le déplacement de l’interface se fait vers l’intérieur de la région glacée. En équations, voilà ce que nous a présenté Alessio dans son exposé :
La question qui nous intéresse ici est de savoir si l’interface eau/glace a tendance a être régulière ou bien possède des « singularités ».
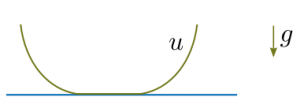
Alessio nous a expliqué que ce problème est intimement lié à un autre problème physique, appelé problème de l’obstacle : considérons une membrane attachée à un bord fermé et soumise à la gravité (par exemple un trampoline un peu mou). On place cette membrane au-dessus d’une table, de telle manière que le bord de la membrane soit au-dessus de la table, mais qu’une partie de la membrane touche la table. La question est de savoir quelle est la forme de la partie de la membrane touchant la table.
Après avoir énoncé quelques résultats historiques concernant ce problème, dont bon nombre avaient été obtenus au moins en partie par le mathématicien argentin Luis Caffarelli, Alessio nous a expliqué sa contribution obtenue en collaboration avec le jeune (et brillant) mathématicien espagnol Joaquim Serra.
Ces résultats peuvent être exploités pour répondre à notre problème de glace qui fond de manière très fine et profonde. Pour chaque temps \(t\), on photographie l’interface eau/glace ; on appelle \(I_t\) cette interface, et on cherche à décrire sa forme. Avec le jeune (et tout aussi brillant) mathématicien espagnol Xavier Ros-Oton, Alessio et Luis ont démontré le théorème suivant 7Qui n’est pas encore publié : c’est un travail en cours ! :
Théorème (Figalli, Ros-Oton, Serra) :
Pour « la plupart » des temps \(t\) 8En termes techniques, en dehors d’un ensemble fermé de dimension de Hausdorff 1/2., l’interface \(I_t\) est aussi lisse que possible 9Pour les mathématiciens, on dit que l’interface est analytique.. Si à un moment \(t\) l’interface \(I_t\) n’est pas lisse, on sait qu’elle ne l’est qu’en dehors d’un petit ensemble de singularités. 10L’ensemble des singularités de dimension \(d\) est « petit », dans le sens où il est inclus dans une sous-variété de dimension \(d\).. On sait de plus classifier ces singularités : elles ressemblent à l’un des trois dessins suivants.
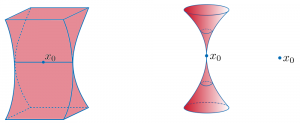
Encore mieux, on peut dire des choses concernant la régularité de l’interface
\(I_t\) au voisinage de (la plupart de) ces singularités…
Alessio a terminé son exposé par une image où on peut observer des singularités comme celles décrites par son théorème. Saurez-vous les retrouver ?
Post-scriptum
Merci à Alessio de m’avoir gentiment autorisé à utiliser les images de son exposé. Bien sûr, s’il y a des erreurs dans l’article, c’est uniquement de ma faute et pas de celle de l’orateur !
ÉCRIT PAR
Pierre-Antoine Guihéneuf
Maître de conférences - IMJ-PRG - Sorbonne Université
