Encore un petit coup de gueule, pour continuer à entretenir ce débat et veiller à ce qu’il ne s’éteigne pas !
Il est vrai que ces dernières années on discute pas mal des problèmes de l’enseignement des mathématiques, mais souvent globalement, et rarement (je dirais même presque jamais) de façon concrète, dans le détail, « au pied du mur » comme on dit. Pour un ouvrier de l’enseignement comme moi, le fait que le débat stagne à ce niveau m’agace. La théorie c’est bien ! mais que vaut-elle si elle ne reste que cela ? On comprend mieux les difficultés quand on regarde de près, n’est-ce pas ?
Par exemple, les inégalités (avec ce qui tourne autour) sont une de ces difficultés. Je ne pense pas me tromper (et les enseignants du secondaire pourraient en témoigner) en disant que beaucoup d’élèves les manipulent moins aisément que les égalités. Pour ces dernières, ils s’en sortent à l’aide de recettes, alors que les inégalités demandent des précautions, et leur utilisation a plus besoin d’être accompagnée d’un raisonnement qualitatif.
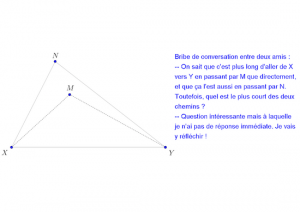
Oui, le raisonnement qualitatif ! Celui-là manque aux apprentis, et surtout aux étudiants des formations préparant à la fonction d’enseignant ! (C’est le cas de ces derniers qui m’intéresse le plus : ils vont enseigner !) Pour illustrer plus clairement ces propos, voici un exercice simple parmi ceux qui montrent qu’il y a problème. (J’ai eu l’occasion
d’en traiter pendant des séances de travaux dirigés.)
Exercice
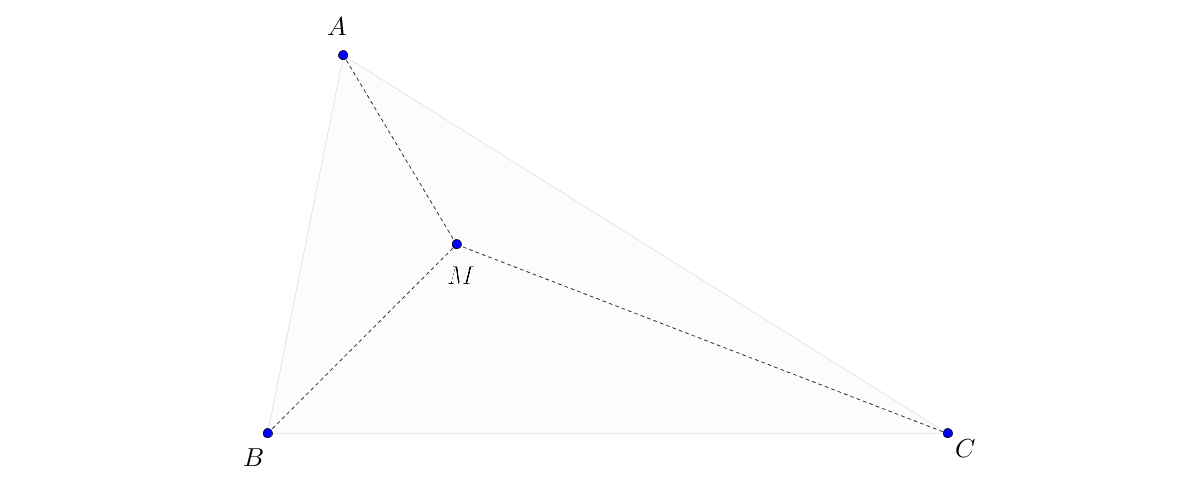
Soit \(ABC\) un triangle (non plat pour écarter une situation immédiate) de périmètre \(p\). Montrer que, pour tout point \(M\) intérieur à \(ABC\),
on a : \({p\over 2}\leq MA+MB+MC\leq p\).
Pour la preuve, je leur ai suggéré d’user de l’inégalité du triangle \(XM+MY\geq XY\) valable pour trois points du plan \(X\), \(Y\) et \(M\) avec égalité \(XM+MY=XY\) si, et seulement si, \(M\) appartient au segment \([XY]\).
1. La relation \(MA+MB+MC\geq {p\over 2}\) est immédiate et presque tous les étudiants sont arrivés à l’établir.
Il leur a suffi d’appliquer la dite inégalité à chacun des triplets \((M,A,B)\), \((M,B,C)\) et \((M,C,A)\) : \[\cases{MA+MB\geq AB\cr MB+MC\geq BC\cr MC+MA\geq CA}\]
et sommer membre à membre pour avoir le résultat escompté. C’est donc l’application immédiate de l'{inégalité du triangle} suivie de simples règles (des recettes) de calcul, une démarche à laquelle ils sont habitués dans l’apprentissage des maths qu’on leur a inculqué.
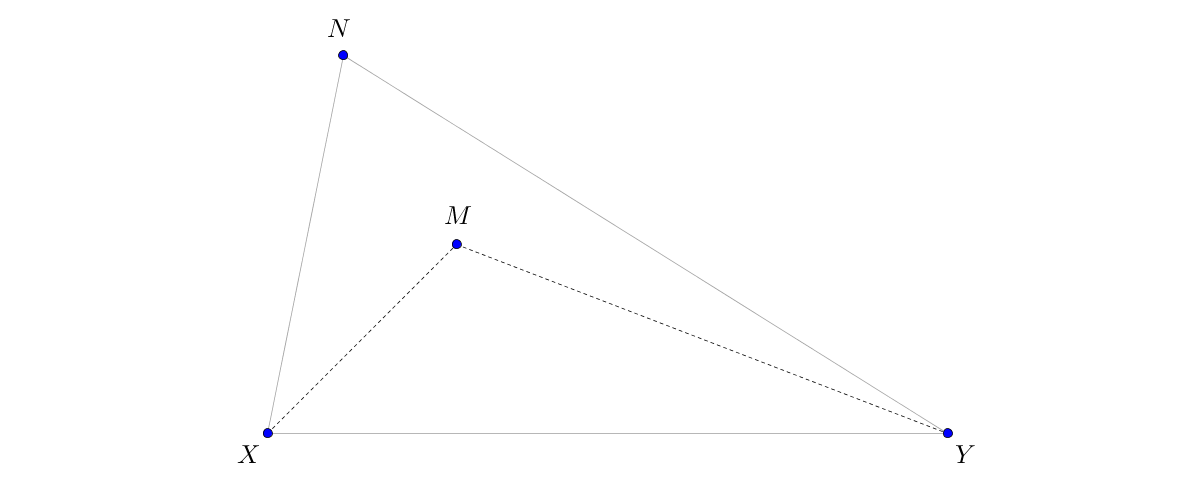
2. Par contre, ils ont calé sur la relation \(MA+MB+MC\leq p\). Beaucoup sont passés par l’inégalité \(MX+MY\leq NX+NY\) (voir figure ci-dessous), et c’est ce qu’il faut faire bien sûr.
Preuve
Pour bien suivre le calcul, il est conseillé de regarder en même temps le dessin. On a :
\[\eqalign{AB+AC&=AB+(AL+LC)\cr
&=(AB+AL)+LC\cr
&\geq BL+LC\cr
&=(MB+ML)+LC\cr
&=MB+(ML+LC)\cr
&\geq MB+MC}
\]
On établit de la même manière les inégalités \(BA+BC\geq MA+MC\) et \(CA+CB\geq MA+MB\). On a donc :
\[\cases{AB+AC\geq MB+MC \cr BA+BC\geq MA+MC \cr CA+CB\geq MA+MB.}\]
En les sommant membre à membre, on obtient \(2(AB+BC+CA)\geq 2(MA+MB+MC)\), c’est-à-dire l’inégalité cherchée :
\[MA+MB+MC\leq p.\]
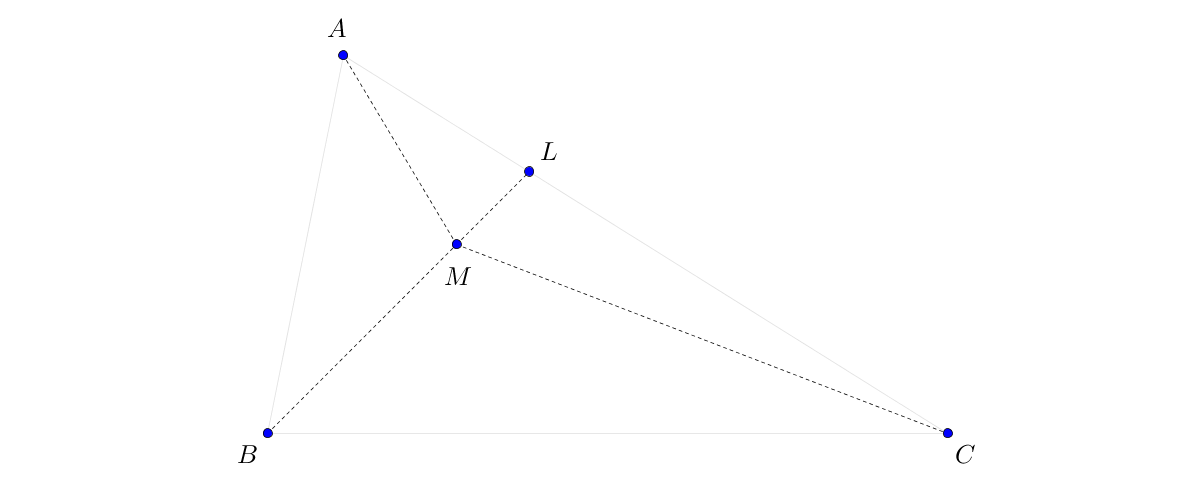
La clé de la preuve est donc le rajout du point \(L\), intersection de la droite \((BM)\) et le côté \(AC\).
C’est souvent ainsi qu’il faut procéder pour résoudre les exercices pour lesquels les recettes toutes faites ne marchent pas ; en particulier en géométrie quand la figure initiale (celle de l’énoncé) s’avère « incomplète ».
C’est un exemple (parmi tant d’autres) sur lequel on voit explicitement les carences, les lacunes et le manque de prise d’initiative chez les étudiants, un sérieux problème dans l’enseignement des maths depuis plus de deux décennies.
Est-il normal qu’un étudiant de Licence 3 ou de Master (surtout un futur enseignant) bloque toujours ? Qu’il pose la plume dès qu’il n’arrive plus à appliquer un mécanisme bien rodé ?
Des questions récurrentes qui lassent, c’est certain. Mais si on cesse de les poser, et de les reposer, on devrait accepter que les choses restent ainsi et qu’il n’y a plus rien à faire pour sauver cet enseignement.
ÉCRIT PAR
Aziz El Kacimi
Professeur émérite - Université Polytechnique Hauts-de-France
