Quelques mots sur les figures sans paroles… I

I. Le théorème de Ceva

La rubrique Figures sans paroles propose régulièrement une figure géométrique (tirée du livre Geometry in Figures par Arseniy Akopyan) avec un minimum de données suggérant un énoncé. Au lecteur d’en formuler un et, si possible, en donner une preuve. Mais depuis sa mise en ligne il y a un peu plus de six mois, les commentaires ou des propositions de solutions y sont presque inexistants. Un billet là-dessus à l’occasion ne serait donc pas inutile et incitera peut-être à une participation plus visible à la vie de cette rubrique. J’espère que le présent texte, et les prochains qui feront sa suite, apporteront une contribution dans ce sens. Je me propose d’y évoquer un thème amusant mais non des moindres de la géométrie plane : les droites concourantes.

Deux droites se coupent presque sûrement. En revanche, trois droites ne sont presque jamais concourantes. Savoir quand elles peuvent l’être est une question fréquente en géométrie élémentaire. On la retrouve dans pas mal de figures de la rubrique évoquée. J’en ai choisi trois : le théorème de Ceva (Figure 4.9.15) sur lequel portera ce premier billet ; le point de Nagel (Figure 2.7) et le point de Gergonne (Figure 2.4) qui seront l’objet du second. Et dans le même ordre d’idées, un troisième billet offrira en supplément quelques friandises géométriques.

Le triangle est la plus élémentaire des figures géométriques non triviales du plan et, sans conteste, l’une des plus riches : pléthore de questions ont été posées et de résultats obtenus dessus. C’est ce qui a fait dire à Crelle en 1816 (suite à la découverte des points de Brocard) « Il est véritablement fascinant qu’une figure aussi simple que le triangle possède des propriétés aussi inépuisables. » Une figure simple, oui !

Il est bien connu que dans un triangle :

(1) – Les médianes concourent en un point \(G\) qui est son centre de gravité.

(2) – Les médiatrices concourent en un point \(O\) qui est le centre de son cercle circonscrit.

(3) – Les bissectrices concourent en un point \(I\) qui est le centre de son cercle inscrit.

(4) – Les hauteurs concourent en un point \(H\) qui est son orthocentre.

A priori, ces droites dites remarquables semblent différentes mais elles ont quelque chose en commun : le partage. La médiane tronçonne le triangle en deux parties de même aire. La bissectrice divise l’angle en deux angles égaux et constitue l’ensemble des points à égale distance des côtés adjacents. La hauteur plonge d’un sommet et casse l’angle plat d’en face en deux angles droits. Les médiatrices se rencontrent en le point à égale distance des trois sommets : leur lieu commun de villégiature, proche autant de l’un que des autres. Tout est bien fait !

Et ce qui est encore plus beau : les trois points \(G\), \(H\) et \(O\) sont sur une même droite appelée droite d’Euler du triangle \(ABC\) ; si on leur adjoint le milieu \(\omega \) du segment \([OH]\), le quadruplet \((G,H,O,\omega )\) devient une division harmonique i.e. \({{\overline{OG}}\over {\overline{OH}}}:{{\overline{\omega G}}\over {\overline{\omega H}}}=-1.\)

Les assertions (1), (2) et (3) sont relativement faciles à démontrer. La quatrième n’est pas aussi directe mais on y arrive en passant par un deuxième triangle\(A’B’C’\) dont les médiatrices sont les hauteurs en question. On le construit en traçant les parallèles aux côtés \(BC\), \(CA\) et \(AB\) passant respectivement par les points \(A\), \(B\) et \(C\) (voir dessin ci-dessous).

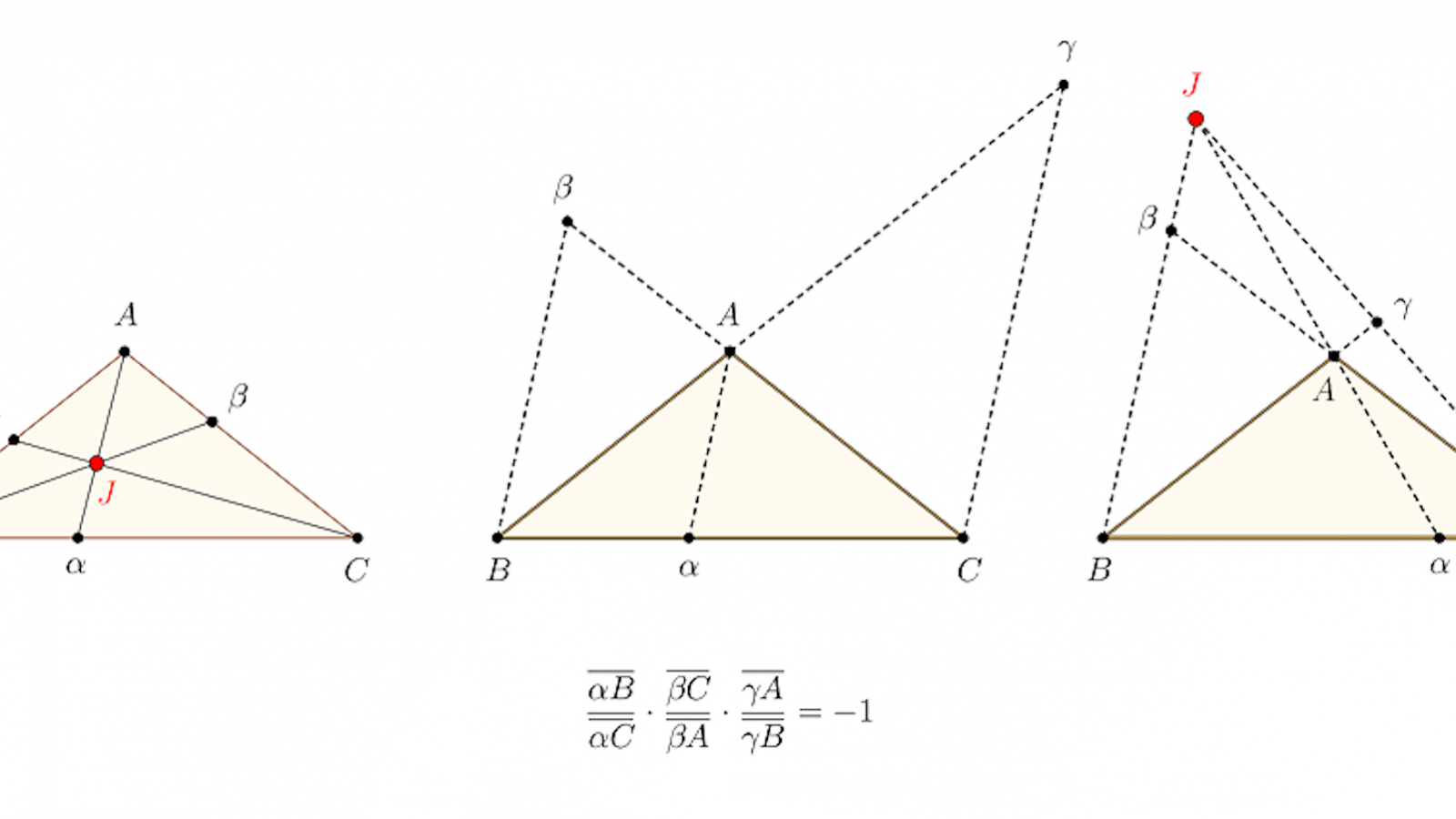
Habituellement on définit une cevienne d’un triangle comme étant une droite qui passe par un sommet et par un point du côté opposé. Mais, pour des « besoins de raccourci » dans ce texte, nous conviendrons d’appeler cevienne toute droite qui passe par un sommet et par un point sur la droite qui porte le côté opposé.
Soit \((A\alpha )\) une cevienne d’un triangle \(ABC\) ; on dira qu’elle est intérieure si \(\alpha \in ]BC[\) et extérieure si \(\alpha \notin [BC]\). (Nous ne nous occuperons pas du cas où le point \(\alpha \) est sur \(B\) ou sur \(C\).) Une question naturelle se pose alors :
Sous quelles conditions trois ceviennes \((A\alpha )\),
\((B\beta )\) et \((C\gamma )\) d’un triangle \(ABC\) sont-elles concourantes ?

Preuve

Aussi bien dans le cas 1 que dans le cas 2, elle est belle et d’un niveau élémentaire. Il faut donc absolument la dévoiler.

En faisant juste de simples dessins le lecteur peut facilement se convaincre que les ceviennes \((A\alpha )\), \((B\beta )\) et \((C\gamma )\) n’ont que deux possibilités si elles veulent être parallèles ou concourantes :
i) les trois sont intérieures ; ii) deux sont extérieures et une est intérieure.
Dans le cas i) les trois rapports \({{\overline{\alpha B}}\over {\overline{\alpha C}}}\),
\({{\overline{\beta C}}\over {\overline{\beta A}}}\) et \({{\overline{\gamma A}}\over {\overline{\gamma B}}}\) sont négatifs.
Dans le cas ii) deux de ces rapports sont positifs et un est négatif.
Il suffit donc de montrer (à chaque fois qu’on aura à le faire) que \({{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1\).

Cas 1. Supposons que les trois droites \((A\alpha )\), \((B\beta )\) et \((C\gamma )\) concourent en un point qu’on notera \(J\). Soit \(A_1\) la projection orthogonale de \(A\) sur la droite \((BC)\). Alors l’aire \({\cal A}(A\alpha B)\) du triangle \(A\alpha B\) est égale à \({{AA_1\cdot \alpha B}\over 2}\) ; de même l’aire \({\cal A}(A\alpha C)\) du triangle \(A\alpha C\) est égale à \({{AA_1\cdot \alpha C}\over 2}\). On a donc :
\[{{\alpha B}\over {\alpha C}}={{{\cal A}(A\alpha B)}\over {{\cal A}(A\alpha C)}}.\]

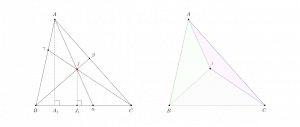
En considérant cette fois-ci la projection orthogonale \(J_1\) du point \(J\) sur \((BC)\) et en suivant la même démarche, on montre que :
\[{{\alpha B}\over {\alpha C}}={{{\cal A}(J\alpha B)}\over {{\cal A}(J\alpha C)}}.\]
Par suite :
\[{{\alpha B}\over {\alpha C}}={{{\cal A}(A\alpha B)}\over {{\cal A}(A\alpha C)}}={{{\cal A}(J\alpha B)}\over {{\cal A}(J\alpha C)}}={{{{\cal A}(A\alpha B)}-{{\cal A}(J\alpha B)}}\over {{{\cal A}(A\alpha C)}-{{\cal A}(J\alpha C)}}}={{{\cal A}(AJB)}\over {{\cal A}(AJC)}}.\]
De façon analogue, on montre que \({{\beta C}\over {\beta A}}={{{\cal A}(BJC)}\over {{\cal A}(BJA)}}\)
et \({{\gamma A}\over {\gamma B}}={{{\cal A}(CJA)}\over {{\cal A}(CJB)}}.\)
D’o\`u :
\[{{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}={{{\cal A}(AJB)}\over {{\cal A}(AJC)}}\cdot
{{{\cal A}(BJC)}\over {{\cal A}(BJA)}}\cdot {{{\cal A}(CJA)}\over {{\cal A}(CJB)}}=1.\]

La réciproque est facile. On suppose qu’on a \({{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1\).
On note \(I\) le point d’intersection des droites \((B\beta )\) et \((C\gamma )\) et \(\alpha’\) le point d’intersection de \((AI)\) avec le segment \([BC]\).
Comme les ceviennes \((B\beta )\) et \((C\gamma )\) sont intérieures, il en est de même de \((A\alpha’)\).
D’après ce qu’on vient d’établir, on a \({{\alpha’B}\over {\alpha’C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1.\)
Comme, par hypothèse, on a aussi \({{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1,\) on en déduit
\({{\alpha B}\over {\alpha C}}={{\alpha’B}\over {\alpha’C}}\). Les deux points \(\alpha \) et \(\alpha’\) étant situés entre \(B\) et \(C\), cette égalité implique qu’ils
sont confondus.

Cas 2. On supposera, pour fixer les idées, \((A\alpha )\) intérieure, \((B\beta )\) et \((C\gamma )\) extérieures.
Ci-dessous les dessins qui serviront de support à tous nos raisonnements.

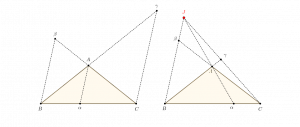
\(\bullet \) On suppose que les droites \((A\alpha )\), \((B\beta )\) et \((C\gamma )\) sont parallèles.

On applique le théorème de Thalès aux droites parallèles \((A\alpha )\) et \((B\beta )\) et aux sécantes \((C\alpha )\) et \((C\beta )\) :

\[{{\beta C}\over {\beta A}}={{BC}\over {\alpha B}}.\]

De même, on applique le théorème de Thalès aux droites parallèles \((A\alpha )\) et \((C\gamma )\) et aux sécantes \((B\gamma )\) et \((B\alpha )\) :

\[{{\gamma A}\over {\gamma B}}={{\alpha C}\over {BC}}.\]

En multipliant ces égalités membre à membre, on obtient \({{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}={{BC}\over {\alpha B}}
\cdot {{\alpha C}\over {BC}}={{\alpha C}\over {\alpha B}}\) qui donne l’égalité cherchée :
\[{{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1.\]

\(\bullet \) On suppose qu’on a \({{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1.\)

Montrons que, si deux ceviennes parmi \((A\alpha )\), \((B\beta )\) et \((C\gamma )\) sont parallèles, alors toutes les trois le sont.
On suppose \((A\alpha )\) et \((B\beta )\) parallèles. Par le théorème de Thalès on a \({{\beta C}\over {\beta A}}={{BC}\over {\alpha B}}.\) D’où
\({{{\alpha B}\cdot {\beta C}}\over {\beta A}}=BC.\) Par suite :

\[1={{{\alpha B}\cdot {\beta C}}\over {{\beta A}}}\cdot {{\gamma A}\over {{\alpha C}\cdot {\gamma B}}}=BC\cdot {{\gamma A}\over {{\alpha C}\cdot {\gamma B}}}\]

qui donne finalement l’égalité \({{BC}\over {\alpha C}}={{\gamma B}\over {\gamma A}}\). Celle-ci montre que les droites \((A\alpha )\) et \((C\gamma )\) sont parallèles
en vertu de la réciproque du théorème de Thalès.

\(\bullet \) On suppose que les droites \((A\alpha )\), \((B\beta )\) et \((C\gamma )\) sont concourantes en un point \(J\).

Nous laisserons alors le lecteur adapter la démonstration du cas 1 pour établir la relation \({{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1.\)

\(\bullet \) On suppose qu’on a \({{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1.\)

Nous laisserons aussi le lecteur adapter la réciproque de la démonstration du cas 1 pour montrer que si deux des ceviennes \((A\alpha )\), \((B\beta )\) et \((C\gamma )\) se coupent en un point \(J\) alors la troisième passe aussi par \(J\).

Les situations géométriques où le théorème de Ceva intervient de façon substantielle sont très nombreuses. Nous en verrons prochainement quelques-unes.