C’est le deuxième billet sur les droites concourantes d’un triangle, à propos de la rubrique Figures sans paroles. Il fait suite au premier qui a initié le sujet autour du Théorème de Ceva. Les applications géométriques de ce théorème sont nombreuses. Nous l’utilisons notamment ici pour établir deux résultats : un dû à Nagel (Figure 2.7) et un autre (Figure 2.4) dans lequel il est impliqué avec Ceva et Gergonne .
Dans un troisième billet, nous offrirons au lecteur, sur à peu près le même thème, quelques friandises topologiques concoctées par des méthodes de géométrie élémentaire plane comme celles dont nous avons usé dans les deux premiers !
Théorème de Nagel.
Soit \(ABC\) un triangle non dégénéré. On note \(\Gamma_1\), \(\Gamma_2\) et \(\Gamma_3\) les cercles tangents aux droites \((AB)\), \((BC)\) et \((CA)\) et extérieurs au triangle \(ABC\). Le cercle \(\Gamma_1\) a \(\alpha \) comme point de contact avec le segment \([BC]\), \(\Gamma_2\) a \(\beta \) comme point de contact avec le segment \([CA]\) et \(\Gamma_3\) a \(\gamma \) comme point de contact avec le segment \([AB]\). Alors les trois segments \([A\alpha ]\), \([B\beta ]\) et \([C\gamma ]\) concourent en un point \(N\) qu’on appelle point de Nagel du triangle \(ABC\).

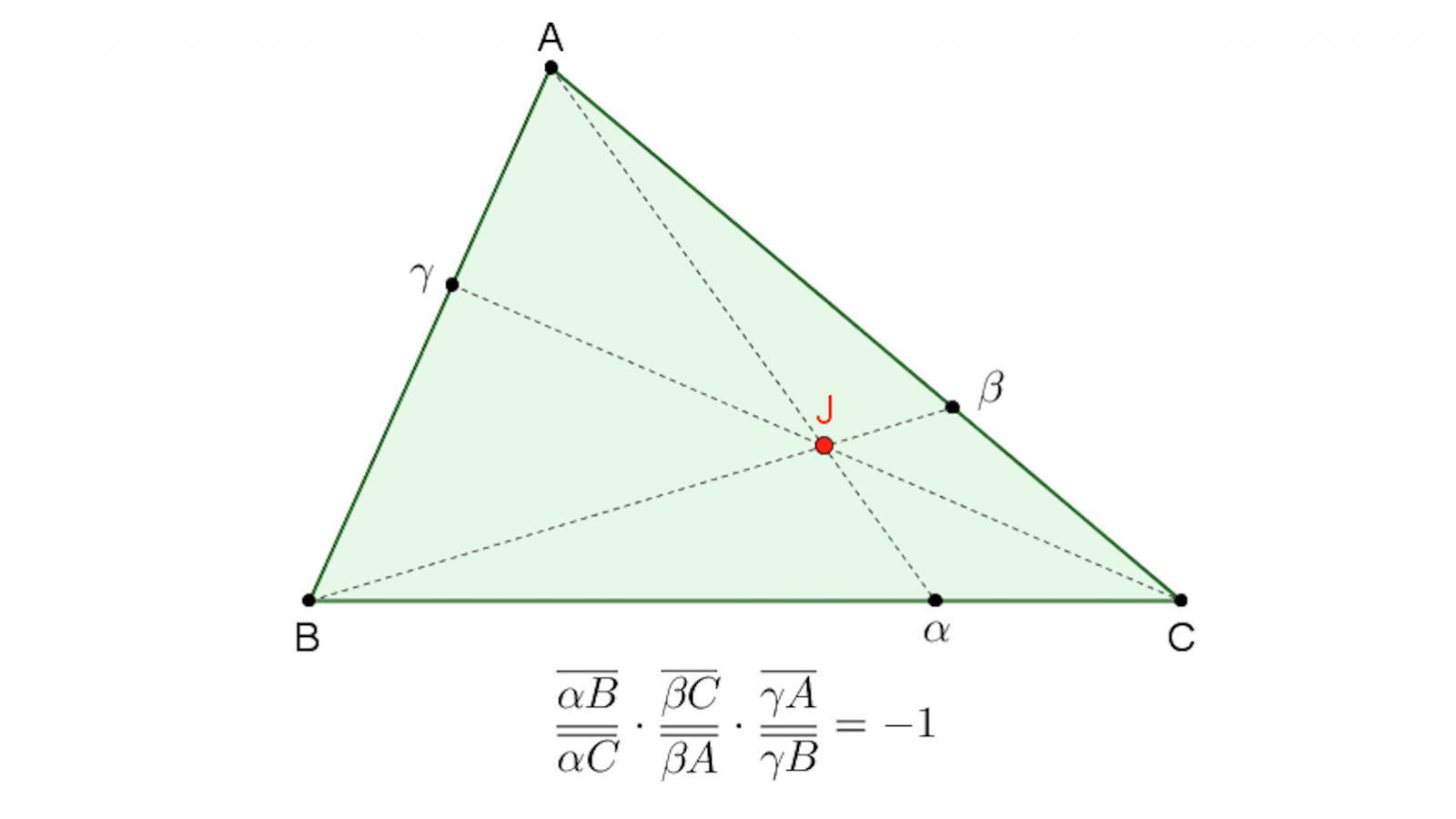
Preuve. D’après le théorème de Ceva (voir les dessins et la formule qui leur est rattachée en haut de cette page), il suffit de montrer que :
\[{{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}=1.\]
\(\bullet \) Les droites \((AB)\) et \((BC)\) étant les tangentes intérieures communes aux cercles \(\Gamma_1\) et \(\Gamma_3\), leur point d’intersection \(B\)
est le centre de l’homothétie négative qui envoie le cercle \(\Gamma_3\) sur le cercle \(\Gamma_1\) ; la valeur absolue de son rapport est \({{R_1}\over {R_3}}\) et envoie \(\gamma’\) sur \(\alpha \). On a donc \({{B\alpha }\over {B\gamma’}}={{R_1}\over {R_3}}\). Mais comme \(B\gamma’=B\gamma \), on a \({{B\alpha }\over {B\gamma }}={{R_1}\over {R_3}}\).
\(\bullet \) De façon similaire, on établit \({{C\beta }\over {C\alpha }}={{R_2}\over {R_1}}\) et \({{A\gamma }\over {A\beta }}={{R_3}\over {R_2}}\).
Ce qui donne finalement :
\[{{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}= {{A\gamma }\over {A\beta }} \cdot {{C\beta }\over {C\alpha }}
\cdot {{B\alpha }\over {B\gamma }}={{R_3}\over {R_2}}\cdot {{R_2}\over {R_1}}\cdot {{R_1}\over {R_3}}=1.\]
Théorème de Ceva-Gergonne-Nagel
Soit \(ABC\) un triangle non dégénéré. On note \(\Gamma \) le cercle inscrit dans ce triangle, \(\alpha \) le point de contact de \(\Gamma \) avec le côté \(BC\), \(\beta \) celui avec le côté \(CA\) et \(\gamma \) celui avec le côté \(AB\). Alors les trois segments \([A\alpha ]\), \([B\beta ]\) et \([C\gamma ]\) concourent en un point \(Ge\) appelé point de Gergonne du triangle \(ABC\).
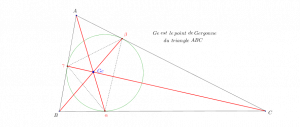
C’est une conséquence immédiate du théorème de Ceva. Il suffit, là encore, de montrer que le produit des trois rapports \({{\alpha B}\over {\alpha C}}\), \({{\beta C}\over {\beta A}}\) et \({{\gamma A}\over {\gamma B}}\) vaut \(1\). À cet effet, remarquons d’abord que, comme les droites \((AB)\) et \((AC)\) sont les tangentes issues de \(A\) au cercle \(\Gamma \), on a \(A\beta =A\gamma \). Pour les mêmes raisons, \(B\gamma =B\alpha \) et \(C\alpha =C\beta \).
D’où :
\[{{\alpha B}\over {\alpha C}}\cdot {{\beta C}\over {\beta A}}\cdot {{\gamma A}\over {\gamma B}}={{\alpha B}\over {\beta C}}\cdot {{\beta C}\over {\gamma A}}\cdot {{\gamma A}\over {\alpha B}}=1.\]




