Qui veut partager des millions ?

« Étant donnés deux millions de points dans un plan, montrer qu’il existe une droite qui partage ce plan en deux parties, dont chacune contient exactement un million de points. »

J’ai appris le problème précèdent au club de préparation aux olympiades de mathématiques, à Bucarest ⁶Il s’agissait, tous les samedis matin, d’une rencontre des élèves de Bucarest qui avaient été récompensés l’année précédente aux olympiades de mathématiques. Le problème précédent avait été proposé par le professeur Florian Colceag.. C’était au début de ma cinquième, lors de ma première participation à ce club, à l’automne 1985 si je me rappelle bien. Je n’ai pas eu le temps de réfléchir moi-même à ce problème, mais seulement d’entendre l’énoncé et, tout de suite après, une solution ⁷Cette solution a été expliquée par Teodor Bănică, à présent lui aussi enseignant-chercheur en France.. Je fus ébloui par le contraste entre l’énormité des données (deux millions ce n’est pas rien !) et la brièveté fulgurante de la preuve. La voici (que celui qui veut y réfléchir tout seul reprenne la lecture plus tard) :

Comme il y a un nombre fini de points, il y a aussi un nombre fini de droites qui les joignent. Prenons alors une direction qui n’est parallèle à aucune d’entre elles. Puis choisissons une droite ayant cette direction et qui se trouve loin des points, les laissant tous d’un seul côté. Faisons-là ensuite bouger parallèlement à elle-même, d’un mouvement qui la rapproche des points. De temps en temps elle passera par l’un d’entre eux. Mais à chaque fois par un seul, car notre hypothèse est que la droite de départ n’est parallèle à aucune des droites joignant deux des points. Lors de son mouvement elle aura dépassé d’abord exactement un point, puis deux, puis trois … Arrêtons-nous après un million. Le problème est résolu !

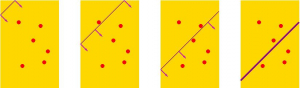
On pourrait bien sûr poser le problème en termes plus généraux, en remplaçant le nombre de deux millions par le syntagme « un nombre pair ». Mais ceci ferait perdre l’impact qu’a sur l’imagination ce grand nombre. Je dirais qu’une partie importante de l’arôme du problème disparaîtrait ainsi ⁸De plus, l’élève perdrait l’occasion d’extraire de la pluralité de propriétés des données, celles qui jouent un rôle dans le problème envisagé. Ici, il ne nous importe pas que deux millions soit divisible par cinq, uniquement qu’il soit pair..

Par exemple, j’ai eu alors le sentiment très puissant que la complexité apparente du monde pouvait en un certain sens être apprivoisée par la pensée. Ce sentiment a été, je crois, l’une des raisons principales qui m’ont fait désirer devenir chercheur en mathématiques. J’y repense maintenant que je suis à la fois chercheur et enseignant, en interaction avec des étudiants qui cherchent leur voie. Cela me fait méditer aux raisons qui m’ont fait choisir la mienne. Je réalise que le problème précédent illustre bien l’importance de poser à nos élèves des questions étonnantes, inhabituelles, aux preuves frappantes de simplicité inventive. Ce type de problèmes peut parler à l’imagination des élèves, leur faire sentir qu’ils auront une vie intérieure riche en s’adonnant aux mathématiques.

Il ne faut pas croire que l’on trouve des solutions si courtes ou élégantes à tous les problèmes auxquels on s’intéresse, bien au contraire. Mais espérer trouver une telle solution est, je crois, un moteur important de la recherche mathématique.

---

Je voudrais revenir à la preuve précédente et commenter certains aspects qui m’étaient invisibles à l’époque. Cette preuve montre qu’en fait, chaque fois qu’on fixe deux nombres dont la somme vaut deux millions, on pourra trouver une droite qui partage le plan en deux parties qui contiennent exactement ces nombres-là de points. Demander d’obtenir des nombres égaux répondait de ce point de vue à un besoin esthétique de symétrie.

C’est ce que je croyais au début de ma réflexion actuelle sur ce problème. Mais en fait il y a une autre raison pour laquelle le bon énoncé demande de partager en deux parties égales.

En effet, on peut se poser la même question dans les trois géométries de dimension deux ⁹Plus précisément, en termes techniques, dans les trois surfaces riemanniennes homogènes, isotropes et simplement connexes. : dans le plan euclidien usuel, dans le plan hyperbolique et enfin sur la sphère. Dans le plan hyperbolique ¹⁰Le lecteur curieux pourra la découvrir dans un article d’Etienne Ghys sur ce site., on peut encore partager en deux parties ayant n’importe quels nombres de points préétablis, bien sûr sous la contrainte que leur somme fasse deux millions. La même preuve qu’avant marche si on remplace les familles de droites de direction donnée dans le plan euclidien par les familles de droites passant par le même point sur le cercle à l’infini du plan hyperbolique.

Mais la situation est différente sur la sphère ! Là, le rôle des droites dans le plan est joué par les grands cercles. On en voit des arcs sur les oranges suivantes.

On se donne donc encore deux millions de points, mais sur une sphère. Ce qui change, c’est qu’il y a maintenant des situations où n’importe quelle droite (grand cercle) qui ne passe par aucun des points, en laisse un million d’un côté et un million de l’autre. Cela arrive lorsque les points apparaissent par couples antipodaux. Ce qui montre que le seul partage qui pourrait être toujours possible dans les trois géométries à la fois est en deux parties égales. Eh bien, un tel partage égalitaire est aussi possible sur la sphère !

Voici comment le voir. On va procéder par analogie avec la preuve précédente. Deux grands cercles se coupent toujours en un couple de points antipodaux, donc on n’a plus de notion de parallélisme. En revanche, on a une notion analogue à celle de famille de droites de direction fixée : c’est celle de famille de cercles passant par le même couple de points antipodaux. On appellera une telle famille un pinceau, et les points communs des cercles qui le composent seront ses pôles (on pourra penser aux méridiens sur un globe terrestre, passant tous par les pôles, et on pourra aussi regarder à nouveau les oranges).

Dans la preuve précédente on considérait une famille de droites telle qu’aucune d’entre elles ne passe par deux des points donnés. Ici on choisira un pinceau tel qu’aucun des cercles qui le composent ne contienne de couple de points non-antipodaux de notre ensemble. Ceci est possible, car deux points non-antipodaux déterminent un unique grand cercle, et qu’il n’y a donc qu’un nombre fini de grands cercles passant par des couples de points non-antipodaux de notre ensemble. Il suffit de choisir les pôles du pinceau en dehors d’eux.

Fixons ensuite l’un des cercles du pinceau qui ne passe par aucun des points donnés, et faisons-lui faire un demi-tour tel qu’à chaque moment il reste dans le pinceau. Suivons ce qui se passe pendant ce demi-tour avec l’un des hémisphères bordés par le cercle (on pourra penser au mouvement de la partie diurne du globe pendant une demi-journée, ou bien au passage d’une nouvelle lune à la pleine lune suivante). On voit alors qu’il existe une situation intermédiaire pour laquelle l’hémisphère contient la moitié des points. En effet, à chaque fois qu’on passe par une position du cercle qui contient des points de l’ensemble donné, le nombre des points de l’hémisphère soit varie de un (si le cercle est passé par un seul point), soit reste inchangé (si le cercle est passé par un couple antipodal). Mais lorsque l’on a fait le demi-tour, on a échangé les deux hémisphères initiaux. On est donc passé par toutes les valeurs intermédiaires entre deux nombres dont la somme fait deux millions, et en particulier par la moitié de ce nombre. Le partage en deux parties égales est donc encore possible !