Règle de trois

La règle de trois est une recette utilisée pour calculer dans des situations de proportionnalité. Son symbole, une croix, n’est pas très intuitif pour décrire une situation que les mathématiciens qualifient de linéaire et qu’ils représentent par une droite. C’est une notion subtile qui se rapproche de celle de fraction.

La proportionnalité

Une situation est proportionnelle lorsque des parts égales contribuent au tout de la même façon.

Exemple. Supposons que pour faire des crêpes pour 8 personnes, il faille

• 250g de farine
• 4 oeufs
• un demi-litre de lait
• 50g de beurre

En divisant en deux parts égales tous les ingrédients, on pourra faire des crêpes pour 4 personnes. Si l’on n’était que 2, on pourrait à nouveau diviser ces quantités en 2, c’est-à-dire :

• 62,5g de farine
• 1 oeuf
• 125ml de lait
• 12,5g de beurre

Si nous faisons 4 tas comportant chacun cette liste d’ingrédients, nous pouvons faire, avec chacun d’eux, des crêpes pour 2 personnes. Avec deux tas, nous retrouvons nos quantités pour 4 personnes et avec 4 tas, nos quantités pour 8 personnes. Et ainsi, si nous étions 6 personnes, il suffirait de prendre 3 de ces tas.

Comme l’oeuf n’est pas divisible en deux parties, avec cette idée, on peut trouver la quantité d’ingrédients pour faire des crêpes pour un nombre pair de convives en prenant autant de tas qu’il y a de couples de convives. Si nous étions un nombre impair, il faudrait soit en prévoir un peu moins, soit un peu plus que la quantité prévue par la recette.

Cette situation peut se résumer par un tableau de proportionnalité

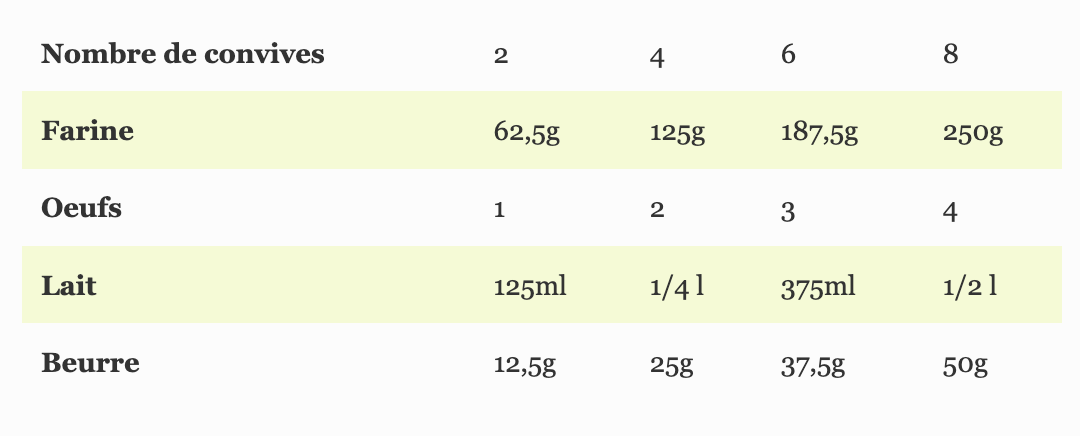
ou encore par un graphique

 

Diverses situations

Certaines situations relèvent de la proportionnalité, ou s’y ramènent, au moins dans une certaine mesure.

• Prendre une échelle commune de mesure permet de raisonner rapidement. Dans l’exemple précédent, l’unité de mesure est le nombre de convives. Mais on aurait pu prendre le nombre d’oeufs, ou la quantité de lait. On est parfois limité par ce que l’on trouve dans son frigo !
• Un autre exemple courant est de convertir en valeur monétaire. Mais très souvent la valeur des objets n’est pas linéaire : elle n’est pas proportionnelle au nombre d’objets. En effet on donne souvent des réductions pour des achats en gros ; autrement dit le prix à l’unité est plus élevé que le prix pour un achat en grande quantité.
• Le plus souvent, une situation ne se révèle donc proportionnelle que dans une certaine limite. On n’envisage pas de faire des crêpes pour un million de convives ; et si on fait des crêpes pour 50 personnes, on n’est pas à 1 oeuf près. D’ailleurs dans notre exemple, il s’agit avant tout d’ordres de grandeur. On prendra un peu plus que 50g de farine et pas nécessairement exactement 62,5g. Les situations courantes sont souvent des situations approchées.

Mais certaines situations ne relèvent pas du tout de la proportionnalité.

• La distance de freinage ne se relie pas simplement au temps de réaction du conducteur. Si il ou elle met deux fois plus de temps à réagir, la voiture parcourra très certainement bien plus que deux fois plus de distance avant de s’arrêter.
• Le temps mis par un athlète n’est pas non plus proportionnel à la distance qu’il parcourt. Le record du monde du 400m est supérieur à deux fois le record du monde du 200m. Au cours d’un 10 000m les premiers tours sont parcourus à des vitesses différentes des derniers tours.
• Le coût d’une course en taxi comporte une prise en charge à laquelle s’ajoute une somme proportionnelle au nombre de kilomètres parcourus.
• Certains phénomènes sont quadratiques. Le poids d’un disque (homogène) de métal n’est pas proportionnel à son rayon, mais au carré de son rayon.

Il existe en fait toute sorte de variation d’une quantité en fonction d’une autre et la situation de proportionnalité est la plus simple, aussi essaye-t-on toujours, quand c’est possible, de s’y ramener.

La quatrième proportionnelle et la règle de trois

La quatrième proportionnelle est le quatrième nombre à mettre dans un tableau de proportionnalité dont 3 cases sur 4 sont déjà remplies. Ce quatrième nombre s’obtient en faisant le produit des nombres situés sur une même diagonale et en divisant par le troisième nombre.