
Si diverses propositions ont été récemment avancées pour résoudre les problèmes de l’enseignement des mathématiques dans le primaire et le secondaire, rien n’est encore réellement acté pour le moment. Une mesure phare préconisée par le rapport Torossian-Villani à cet effet est la formation continue des enseignants. Elle a été évoquée en priorité pour le primaire parce que les étudiants préparant le concours du Professorat des Écoles ont en majorité un cursus littéraire (J’en ai parlé dans ce billet).
C’est déjà ça ! mais ils ne sont malheureusement pas les seuls à avoir besoin d’une remise à niveau : beaucoup d’enseignants du secondaire recrutés récemment (depuis peut-être dix ans ou un peu plus) ont de sérieux problèmes au niveau des connaissances supposées requises pour dispenser correctement une leçon de maths. C’est le constat malheureux que j’ai pu faire : chaque année je vois comment ils sont avant d’intégrer leur fonction. Depuis le début de ma carrière d’enseignant à l’université et jusqu’à maintenant (je suis en passe de prendre ma retraite), je consacre au moins la moitié de mon service d’enseignement aux formations préparant aux divers concours d’accès au métier d’enseignant. Je sais donc de quoi je parle (et j’en suis triste) !
Pour étayer mes propos (que j’assume totalement), voici une série d’exercices du programme du secondaire parmi ceux que j’ai proposés ces dernières années lors d’épreuves d’évaluation et sur lesquels presque tous les étudiants ont eu des difficultés. Ils ont calé dessus, comme on dit en langage parlé ! (« Presque » signifie tous à part au plus cinq sur un effectif d’une quinzaine.)
Exercice 1
Deux robinets \(R_1\) et \(R_2\) alimentent à débits constants un bassin d’eau. Pour le remplir, il faut un temps \(t_1>0\) quand on utilise \(R_1\) seul et un temps \(t_2>0\) quand on utilise \(R_2\) seul.
On se propose de calculer le temps \(t\) que mettent \(R_1\) et \(R_2\) pour remplir le bassin quand on les ouvre en même temps (à leurs débits respectifs habituels) ?
[Il y a plusieurs façons de résoudre ce problème, toutes basées sur le même principe. Quelle que soit celle dont on procède, on doit détailler ses
étapes et expliquer tout ce qu’on fait.]
1 – On pose le problème à des élèves de Troisième. Quelle méthode pourraient-ils utiliser pour le résoudre ?
2 – On pose le problème à des élèves de Terminale. Quelle méthode (autre que celle qui précède bien sûr) pourraient-ils utiliser pour le résoudre ?
Là on voit bien qu’ils ne maîtrisent pas la notion de proportionnalité. À une certaine époque, on résout ce genre de problème en usant de la bonne « règle de trois » qui n’a jamais vieilli malgré qu’on la perçoit de nos jours comme quelque chose de ringard !
Exercice 2
On se donne un nombre \(\alpha >0\) et deux points distincts \(B\) et \(C\) du plan euclidien.
On note \(b\) la distance entre \(B\) et \(C\). (On peut penser au nombre \(\alpha \)
comme la longueur d’un segment \([UV]\) supposé donné.)
Donner le lieu, et dire comment le construire géométriquement, de tous les points \(A\) pour lesquels les triangles \(ABC\) ont pour aire \(\alpha \).
Là on constate un manque de culture en géométrie élémentaire plane. Même la formule donnant l’aire d’un triangle n’est pas acquise et encore moins la volonté d’essayer de la retrouver. Incroyable !
Exercice 3
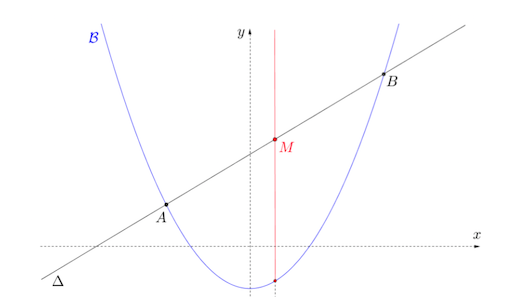
Dans \({\Bbb R}^2\), muni de son produit scalaire usuel, on considère la parabole \({\cal B}\) d’équation \(y=x^2+q\) où \(q\in {\Bbb R}\) et une droite \(\Delta \) d’équation cartésienne \(y=ax+b\) avec \(a>0\).
1 – Sous quelles conditions (portant sur les paramètres \(q\), \(a\) et \(b\)) la parabole \({\cal B}\) intersecte-t-elle la droite \(\Delta \) en exactement deux points \(A\) et \(B\) ?
On note \(M\) le milieu du segment \([AB]\).
2 – On garde le paramètre \(a\) fixe et on fait varier \(b\). Montrer que le point \(M\) varie sur une demi-droite ouverte que l’on déterminera.
Leur incapacité à résoudre cet exercice montre plusieurs de leurs défaillances, entre autres
– difficulté à comprendre que lorsqu’on se donne un repère dans le plan, il y a une correspondance biunivoque entre les points et les couples de réels (étonnant ! n’est-ce pas ?) ;
– quand on impose à un point d’être sur une figure particulière \({\cal B}\) (par exemple notre parabole), on impose à ses coordonnées de vérifier une certaine relation (en l’occurrence \(y=x^2+q\) dans notre exercice) qu’on appelle {{équation cartésienne}} de \({\cal B}\) ;
– imposer à un point d’être sur deux figures géométriques à la fois (par exemple la parabole \({\cal B}\) et la droite \(\Delta \) comme dans le logo), c’est imposer à ses coordonnées de vérifier simultanément leurs équations respectives.
Exercice 4
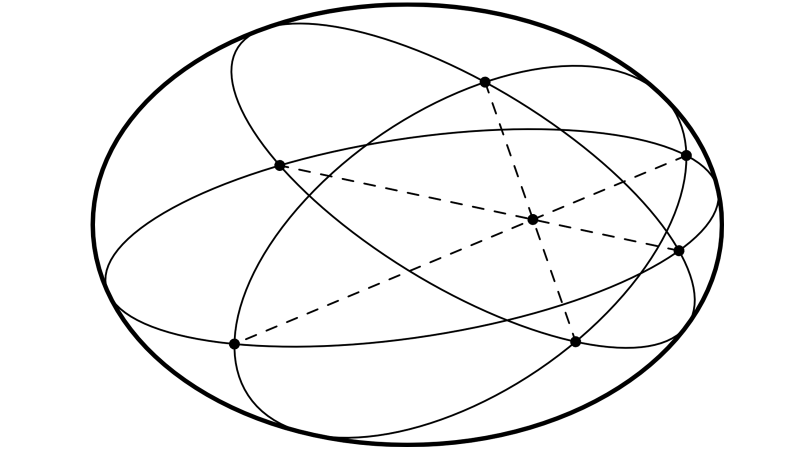
Soit \({\cal C}=ABCDEFGH\) un cube (voir dessin ci-dessous). Les diagonales \((AF)\), \((BE)\), \((CH)\) et \((DG)\) sont-elles des axes de symétrie de \({\cal C}\) ? (Justifier la réponse.)

Cet exercice peut paraître plus difficile mais quand on y réfléchit un tout petit peu, on s’aperçoit en fait qu’il est assez facile. Il y a plus de vingt ans, j’étais à une soirée
au cours de laquelle j’ai fait la connaissance d’un inspecteur d’école primaire. Dès qu’il apprit que je suis enseignant de maths, il s’est mis en tête de me tester en me posant la même question.
Je n’ai pas su répondre au bout du court instant qu’il m’a laissé : j’avais besoin d’un peu plus de temps pour imaginer la figure et bien la « regarder ». Ce que je fis quelques minutes après mais la discussion a vite bifurqué vers autre chose. Je n’ai pas exigé de mes étudiants d’être rapides (je ne l’ai pas été). J’ai simplement voulu qu’ils prennent le temps de réfléchir (je leur en ai donné suffisamment) et espéré qu’ils
procèdent comme suit :
– supposer par exemple que la droite \((AF)\) est un axe de symétrie ;
– en déduire qu’elle l’est aussi pour la figure tracée sur le cube par tout plan la contenant ;
– en particulier pour le rectangle \(ACFH\) dont elle est une diagonale ;
– mais ceci est impossible puisque \(ACFH\) n’est pas un carré ;
– donc \((AF)\) n’est pas axe de symétrie du cube \({\cal C}\).
Mais malheureusement ils ne l’ont pas fait !
Ceci montre, et plus que concrètement, ce que sont les lacunes réelles de ces étudiants, et qu’ils gardent même quand ils arrivent enseignants dans le secondaire, les laissent en héritage à leurs élèves qui les trimballent à leur tour jusqu’au niveau du supérieur. Là, étudiants, pas mal d’entre eux finissent en Master MEÉF, réussissent le concours du CAPES et les retransmettent à leurs apprentis ! Et ainsi de suite…! Mais c’est tabou, paraît-il, de parler de tout cela ! Et quand on le fait, on roule au pas en préférant nuancer les propos !
Toutefois, je tiens à préciser que ni ces étudiants ni les enseignants qu’ils deviennent ne portent la responsabilité directe de cette situation.
Ils sont des victimes de la campagne de dénigrement qu’ont subie les mathématiques (voir ici) : ceux qui l’ont initiée n’avaient pas eu le réflexe d’imaginer que ses effets se transmettront d’année en année et occasionneront des dégâts considérables à l’enseignement de la discipline (et jusqu’à nos jours !)
Une formation continue est donc aussi nécessaire à une majorité d’enseignants du second degré recrutés ces dernières années. Si on en accepte l’idée et le principe, on dégagera facilement plusieurs pistes de travail. Il suffit simplement de se donner les moyens matériels pour sa mise en œuvre effective sur le terrain.
Il paraît qu’une réforme de la « Préparation au CAPES » est en cours d’étude (voir par exemple ici ou là). Le ministre de l’Éducation nationale y recommanderait de mettre le concours d’admissibilité en fin de Licence 3 et les épreuves d’admission en fin de Master 1. C’est une bonne idée à mon avis, mais à condition qu’elle
soit accompagnée de la création d’une filière débutant en Licence 2, complètement dédiée à la formation des enseignants du secondaire et une refonte substantielle des programmes :
– En mathématiques bien sûr avec un bon contenu, adapté et rechargé de géométrie (qui est la colonne vertébrale des mathématiques, qu’on le veuille ou non !)
– Mais aussi en français. Les rédactions sur les copies laissent vraiment à désirer au niveau de l’orthographe, la grammaire, la construction des phrases… Il faut même quelquefois jouer à la devinette pour comprendre ce que l’auteur cherche à dire !
« Un enseignant ne devrait pas être comme ça » !
Vos commentaires sont les bienvenus !




8h51
Voir les 5 commentaires