
Le jeu des pousses, Sprouts en anglais (ce qui signifie germes), se joue à deux joueurs avec un papier et un crayon. Initialement, il y a un nombre quelconque de points répartis au hasard sur une feuille de papier. Alternativement, chaque joueur doit :
- tracer une ligne entre deux points (ou d’un point à lui-même pour former une boucle),
- ajouter un nouveau point n’importe où sur la ligne qu’il vient de tracer.
Les joueurs doivent respecter les règles suivantes :
- les lignes peuvent être droites ou courbes, de longueur quelconque, mais en aucun cas ne peuvent s’intercepter ;
- le nouveau point ne peut être à l’extrémité d’une ligne, il doit être sur la ligne ;
- d’un point ne peuvent émerger qu’au maximum trois lignes.
Le premier joueur qui ne peut plus jouer a perdu.
La figure ci-dessous montre une partie avec 2 points initiaux (pour plus de détails, voir cette page).
-

Exemple d’une partie du jeu de Sprouts, avec 2 points de départ. Le deuxième joueur gagne.
Une partie donne parfois lieu à un dessin inattendu, comme par exemple :
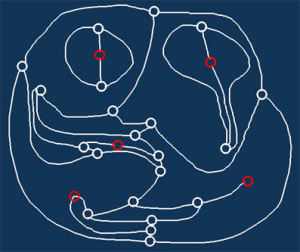
Les points rouges représentent les points morts, qui ne peuvent plus être joués.
Le jeu des pousses a été inventé par John Conway et Michael Paterson dans les années 1960, et fut décrit pour la première fois en 1967 par Martin Gardner dans sa rubrique du Scientific American. Michael Paterson est un expert en informatique théorique, notamment dans l’élaboration d’algorithmes et dans l’analyse de leur complexité. Il a joué un rôle important à la fin des années 1960 pour aider à faire reconnaître l’informatique en tant que discipline scientifique. John Conway est un mathématicien qui a travaillé dans de nombreux domaines : théorie des nombres, des nœuds, des groupes finis, et en théorie des jeux combinatoires, pour laquelle ses travaux sont les plus connus. Il n’est alors pas étonnant de retrouver le jeu des pousses (Sprouts) dans l’ouvrage Winning Ways for Your Mathematical Plays, co-écrit par Conway, Elwyn Berlekamp et Richard Guy (publié en 1982 après quinze années d’écriture).
Le jeu des pousses occupe un des vingt-cinq chapitres de l’ouvrage, dans lequel est analysée la version présentée ci-dessus, ainsi que d’autres variantes. Peu de pages sont consacrées à chacune de ces variantes, exception faite du Lucasta, duquel les auteurs « sont tombés amoureux ». Cette variante du jeu de pousses actuel fut introduite par Édouard Lucas (1842-1891) dans le troisième tome de ses Récréations mathématiques, dont la première édition date de 1883. Le nom Lucasta a été donné par les auteurs de Winning Ways, en hommage à Lucas qui lui la nomme le jeu des jonctions de points. Toutefois, nous ne pouvons affirmer si le jeu des jonctions de points a été découvert par Conway après l’invention du Sprouts dans les années 1960 ou s’il s’en est inspiré. Voici la définition et les règles du jeu données par Lucas :
Étant donné un nombre quelconque de points, deux joueurs se proposent la partie suivante : chacun d’eux, à tour de rôle, joindra deux points par un trait mené à volonté, en évitant toutefois de passer par un autre point, et en observant :
- Que chaque point ne serve jamais d’extrémité à plus de deux traits ;
- Que d’un point à un autre, il ne soit jamais mené qu’un seul trait ;
- Qu’un trait ne se croise jamais avec un autre, ni avec lui-même. (On suppose que les traits sont des lignes sans épaisseur.)
Le premier des deux qui ne pourra plus jouer aura perdu la partie. (pp. 99-100)
Lucas précise que ce jeu a été étudié par Camille Flye Sainte-Marie et Henri Delannoy 6Henri Delannoy a résolu de nombreux problèmes présentés par Lucas dans ses Récréations mathématiques. Un colloque en son hommage s’est tenu en octobre 2015 et avait donné lieu à un billet dans la tribune des mathématiciens. Les actes de ce colloque paraîtront prochainement aux éditions PULIM de Limoges : Barbin Évelyne, Goldstein Catherine, Moyon Marc, Schwer Sylviane et Vinatier Stéphane. (Eds.). Les travaux combinatoires en France (1870-1914) et leur actualité : un hommage à Henri Delannoy. Limoges, PULIM.. Flye Sainte-Marie aurait notamment travaillé sur les fins de parties du jeu des jonctions de points, et fourni un travail très complet, mais « dont les développements ne peuvent trouver ici leur place » (p. 99). L’une des caractéristiques d’un billet pour la tribune des mathématiciens étant sa courte taille, et pour suivre la pensée de Lucas, « nous nous contenterons d’indiquer, d’après M. Delannoy, la marche à suivre pour gagner sûrement, en jouant correctement dès le début de la partie. »
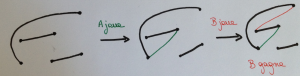
Dans un premier temps, Lucas remarque que si un joueur, appelons-le A, joint un trait à un trait (c’est-à-dire deux points qui ne sont pas isolés), son adversaire, B, peut riposter en fermant la chaîne, c’est-à-dire en joignant les deux points situés aux extrémités. Il n’y a alors plus de coups possibles pour A, il perd.
-

Si A joint un trait à un trait, B ferme la chaîne et gagne.
Lucas s’intéresse donc à la jonction d’un point isolé à un autre, d’un point isolé à un trait et à la continuation d’une chaîne. De ces premières considérations, Lucas conclut que la partie sera perdue par le joueur à qui on laisse un jeu qui ne contient que des traits (sans points isolés) ou bien un jeu qui ne contient que des traits et un seul point isolé.
-
Si le jeu n’est constitué que de traits, A perd, car d’un point à un autre ne peut être mené qu’un seul trait.
-
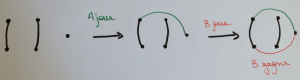
Si le jeu n’est constitué que de traits et d’un seul point isolé, A perd, car d’un point à un autre ne peut être mené qu’un seul trait.
Lucas détermine ensuite l’issue d’une partie du jeu des jonctions de points selon le nombre de points initiaux, que nous noterons \(N\), et considère quatre cas selon les restes de la division euclidienne de \(N\) par 4 : \(N = 4n\), \(N = 4n+1\), \(N = 4n+2\) et \(N = 4n+3\). Après une analyse des cas particuliers où \(n = 0\) et \(n = 1\), Lucas explique comment le deuxième joueur, B, peut gagner la partie quand \(N\) est pair (\(N = 4n\) et \(N = 4n+2\)) ou quand \(N = 4n+1\).
En résumé, A gagnera quand le nombre de points donnés sera égal à 2 ou à un multiple de 4 moins 1 ; il perdra dans tous les autres cas, si l’on joue correctement. Il y a donc un désavantage marqué à jouer le premier quand le nombre de points donnés est inconnu. Il y a alors trois à parier contre un que le premier joueur perdra la partie. (p. 103)
Ainsi, le Lucasta est un jeu dit « résolu » : il est possible de donner une stratégie complète à partir de n’importe quelle position initiale, à la fois en version normale (le premier joueur qui ne peut plus jouer perd) et en version misère (le premier joueur qui ne peut plus jouer gagne).
Le jeu des pousses, inventé 70 années plus tard par Conway et Paterson, consiste donc en une légère modification du jeu des jonctions de points de Lucas : trois traits peuvent émerger d’un point (au lieu de deux), un nouveau point est créé sur le trait nouvellement tracé et un trait peut relier un même point (pour faire une boucle). Pourtant cette modification entraîne une sérieuse complexification dans la résolution du jeu des pousses. On peut y voir là une signature de Conway qui aime présenter des problèmes ou des jeux apparemment simples, mais qui dévoilent une complexité sous-jacente dans leur analyse, parfois insoupçonnée 7C’est le cas par exemple du jeu de la vie. Voir également l’article sur les jeux et les nombres surréels.. Martin Gardner fut le premier en 1967 à faire état de la résolution manuelle du jeu des pousses avec 6 points de départ, analysée en une cinquantaine de pages par Denis Mollison 8Voir l’article de 1967 : Martin Gardner, Mathematical games of Sprouts and Brussels Sprouts : games with a topological flavor, Scientific American 217 (July 1967), pp. 112-115, ainsi que Martin Gardner, Mathematical Carnival, The Mathematical Association of America, réédition de 1989, pp. 3-11.. Il faut en revanche attendre quelques années avant que les informaticiens David Applegate, Guy Jacobson et Daniel Sleator s’intéressent à la programmation du jeu et obtiennent une résolution faible 9En théorie des jeux combinatoires, on peut nuancer le niveau de résolution de tel ou tel jeu : un jeu est résolu si son issue (victoire, défaite ou nul) peut être parfaitement connue dès la position initiale. On dit que la résolution est faible s’il est possible de fournir un algorithme donnant un jeu complet qui soit optimal pour l’un des joueurs, quels que soient les coups joués par l’adversaire, mais l’algorithme ne corrige pas son jeu selon les erreurs de l’adversaire. La résolution est dite forte si on peut fournir un programme qui joue parfaitement chaque coup à partir de n’importe quelle position, même si des erreurs sont commises par un des joueurs. avec 11 points de départ en 1991.
La difficulté première vient du problème de représenter le jeu, qui se joue initialement avec un papier et un crayon, sous une forme permettant à l’ordinateur de calculer les coups. Il existe en effet une infinité de chemins entre deux points du plan et la première étape est d’identifier les positions qui sont égales à déformation près (homéomorphisme du plan sur lui-même). Cette complexité explique la désaffection du jeu pendant près de vingt ans, avant que Julien Lemoine et Simon Viennot ne réactivent les travaux déjà menés et améliorent considérablement les programmes. En 2007, ils résolvent le jeu jusqu’à 32 points de départ, puis jusqu’à 44 points de départ en 2011, ainsi que quelques valeurs isolées jusqu’à 53 points de départ. Chacune des issues calculées vérifie la « conjecture du Sprouts » émise par Applegate, Jacobson et Sleator : « la position de départ à p points est perdante si et seulement si p est congru à 0, 1 ou 2 modulo 6. »
Avec son jeu des jonctions de points, Édouard Lucas fournit un nouvel exemple de récréation mathématique 10D’autres articles et billets sont consacrés aux récréations de Lucas, voir par exemple, l’éventail mystérieux, les tours de Hanoï, ou encore le jeu du Taquin.d’un autre siècle dévoilant une richesse mathématique qui continue d’inspirer et de faire réfléchir mathématiciens et informaticiens.




