Défi de la semaine
Trouver cinq entiers strictement positifs consécutifs ayant la propriété suivante : la somme des carrés des deux plus grands nombres est égale à la somme des carrés des trois autres nombres.
Solution du 3e défi de septembre 2023
Réponse :
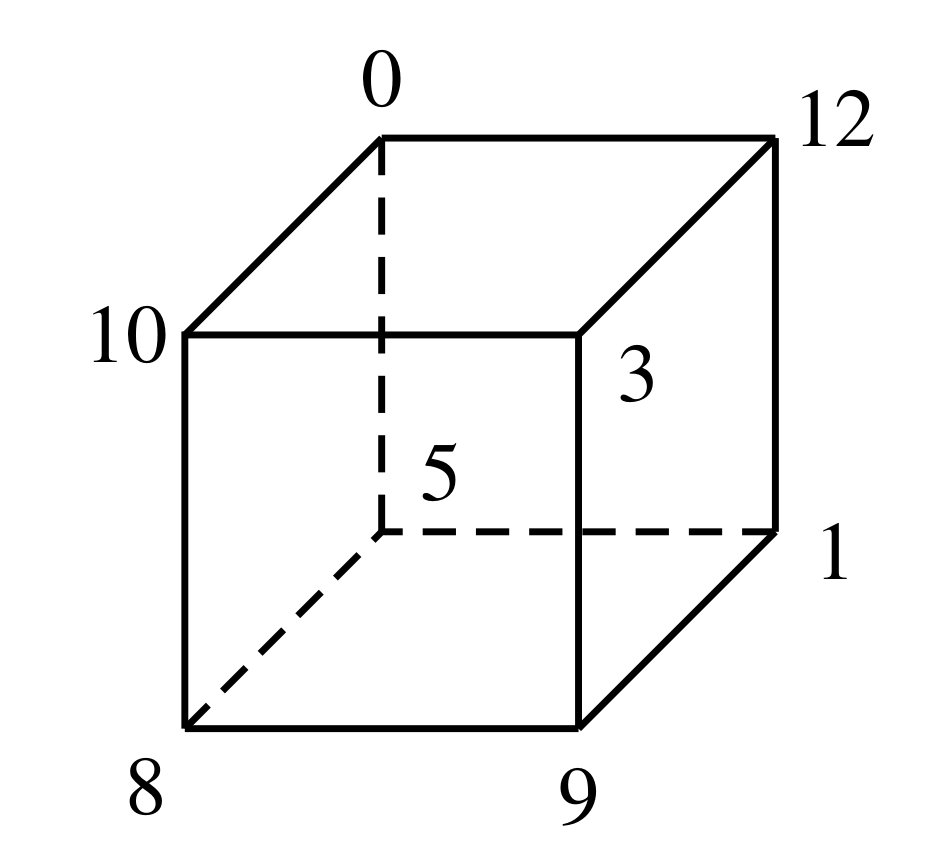
Comme \(12\) est une des différences, les nombres \(0\) et \(12\) doivent être placés sur deux sommets adjacents du cube.
Comme \(11\) est une autre différence, soit \(1\) est placé sur un sommet adjacent au sommet contenant le nombre \(12\), soit \(11\) est placé sur un sommet adjacent au sommet contenant \(0\).
Supposons que le sommet \(1\) soit sur un sommet adjacent au sommet étiqueté par \(12\). Alors, une possibilité est la suivante :
Post-scriptum
Le calendrier est publié aux Presses Universitaires de Grenoble, sous la direction scientifique de Romain Joly.
Crédits images
©JROBALLO / Adobestock
ÉCRIT PAR
Romain Joly
Maître de conférences - Institut Fourier de Grenoble
10h31
Les deux plus grands nombres sont consécutifs, donc de parité opposée. La somme de leurs carrés est alors impaire, et ainsi Il y a un seul nombre impair parmi les trois autres, et c’est forcément le deuxième. On cherche donc \(n>0\) tel que \[(2n)^2 + (2n+1)^2 + (2n+2)^2 = (2n+1)^3 + (2n+1)^4\]
Après simplification on obtient \(n^2 -4n -5 = 0\), dont la seule solution positive est \(n=5\), ce qui donne les nombres \(10,11,12,13,14\), et en effet on peut vérifier que \(10^2 + 11^2 + 12^2 = 365 = 13^2 + 14^2\)
10h34
Oups ! Erreur de copier coller 🙂
\[(2n)^2+(2n+1)^2+(2n+2)^2=(2n+3)^2+(2n+4)^2\]
19h06
Afin de tenter de calculer facilement le trinôme du 2nd degré, je prends \(x-1\), \(x\) et \(x+1\) pour les trois plus petits entiers ce qui donne rapidement \(3x^2+2\) pour la somme de leurs carrés ; je calcule pas trop difficilement pour les deux entiers les plus grands une somme de carré égale à \(2x^2+10x+13\).
Alors \(x^2-10x-11=0\) a pour solution \(x=11\).
Les cinq entiers sont donc \(10\), \(11\), \(12\), \(13\) et \(14\).
23h36
n²+(n+1)²+(n+2)²=(n+3)²+(n+4)²
— > n²-8n-20=0
n=10
Les 5 nombres : 10, 11, 12 ,13, 14
8h54
Il me semble que le plus simple est de prendre n-2, n-1, n, n+1 et n+2..
Après développements et simplification on obtient n² = 12n soit n = 12
( n = 0 conduisant à la solution triviale mais interdite ici -2, -1, 0, 1 et 2
9h24
Ah oui !
Définitivement la plus simple puisque pas de trinôme !
Bravo pour le coup d’œil 🙂 !!!