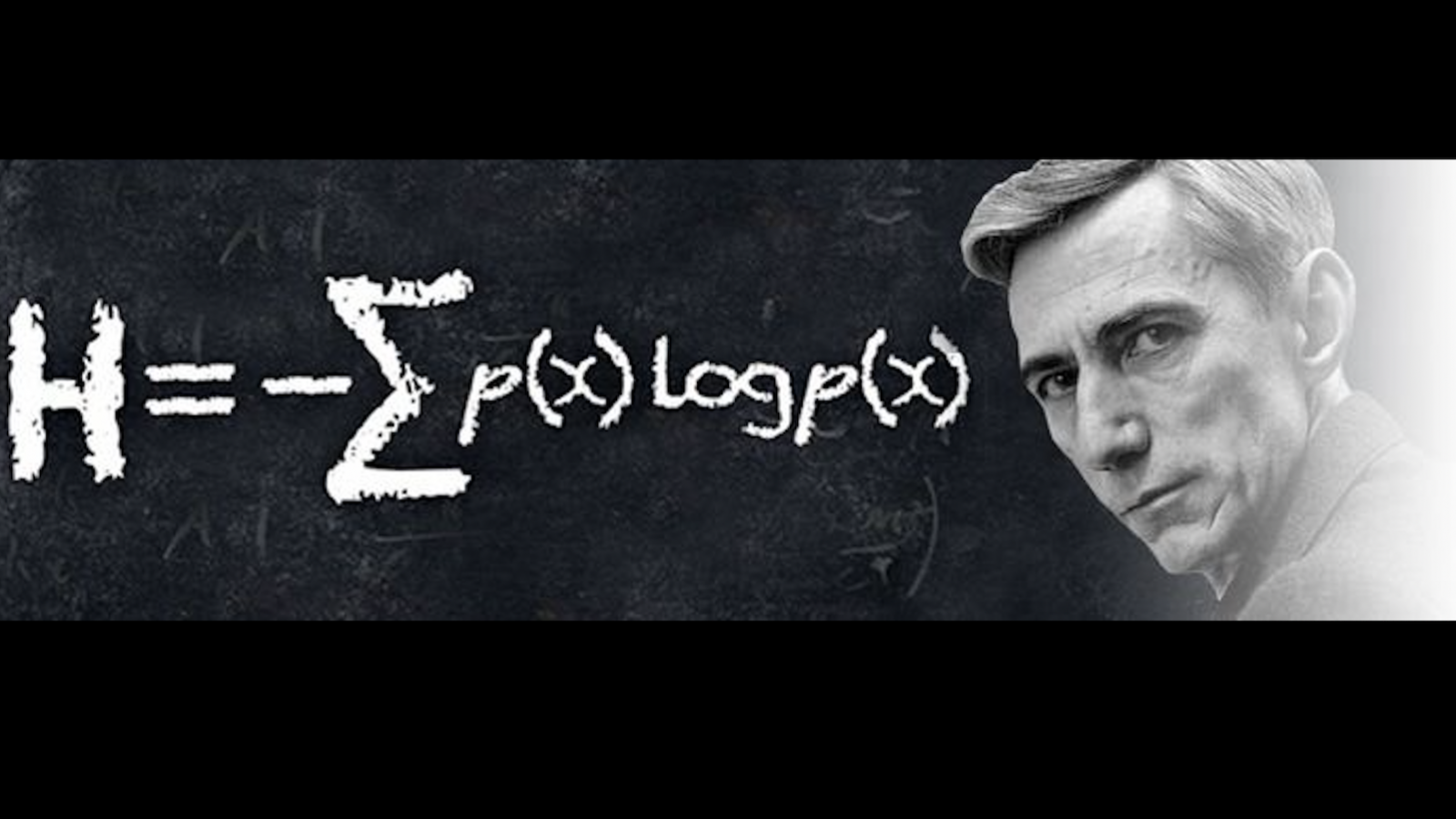
En 1948, le mathématicien et ingénieur américain Claude Shannon crée la théorie de l’information, reliant diverses branches : mathématiques (probabilités, combinatoire, cryptographie), physique (électronique et théorie du signal) et techniques informatiques (compression de données). Cet article présente le contexte historique de ce sujet : la théorie de l’information a accompagné les progrès technologiques de la fin du vingtième siècle. Il introduit ensuite les notions de sources et de canaux d’information.
Théorie de l’information et progrès des 20ème et 21ème siècles
Quand Claude Elwood Shannon (1916-2001) développait sa théorie dans les années 40, la découverte du transistor en 1947 donna un nouvel élan à l’électronique : il s’agissait d’améliorer les liaisons radio ou TV, et les détections radar.

Puis l’informatique se développait par vagues successives. Les premiers ordinateurs fonctionnaient à tubes dans les années 40, remplacés par les transistors (années 50), les circuits intégrés (années 1960) et les microprocesseurs (années 70).
Avec l’informatique, de nouveaux besoins apparaissaient : comprimer les données pour pouvoir les stocker sur des supports alors rares et chers.
Les communications par satellites se développaient depuis les années 60. Il fallait multiplier le nombre de liaisons simultanées avec des puissances limitées.
Puis les liaisons optiques terrestres et maritimes remplaçaient celles coaxiales et hertziennes depuis les années 90.
Depuis les années 80, coder images et sons, et avec le minimum de symboles binaires tout en garantissant la qualité, était un sujet quotidien pour tous.
Si la théorie de l’information n’a pas à elle seule réalisé toutes ces évolutions, elle a accompagné leurs progrès. Si vous réalisez deux choses bien différentes, un nouveau type de modem et un autre de zippage d’un fichier, leurs performances seront comparées aux limites prédites par la théorie de l’information.
Objectif de l’article
Après une courte présentation de la notion d’information au sens de Shannon, on introduit la notion fondamentale de canal. Une information nous parvient parfois de façon altérée ou partielle. Le peu qui nous en reste est-il suffisamment fidèle pour nous forger une opinion ou prendre une décision ? Si C. Shannon s’est intéressé aux télécommunications, on développera des exemples touchant à d’autres domaines des probabilités.
L’information vue par Shannon
Claude Shannon a eu l’idée de définir l’information et différents autres concepts originaux. Avant de traiter les canaux, l’article présentera la notion de sources d’information.
Information
La notion d’information définie par Shannon est un peu différente de celle de la vie quotidienne.
La réalisation d’un événement parmi \(N\) possibles signifie que l’on obtient une {information}. Celle-ci sera d’autant plus grande que l’événement sera imprévisible. Par définition, on fixe :
\[i = \log_2\left( {1\over p}\right) = -\log_2 (p)\]
où \(p\in ]0,1]\) est la probabilité de cette réalisation. Cette {quantité d’information} \(i\) (positive puisque le nombre \(\log_2 (p)\) est négatif quelle que soit la probabilité traitée) est souvent exprimée en {shannon} (\(\text{Sh}\)) [[En réalité, Shannon utilisa le terme “bit”, contraction de “binary digit”. Ce terme s’étant généralisé, on préfère utiliser en théorie de l’information le terme “shannon”. On note que suivant la théorie de Shannon, on ne peut pas traiter moins de deux événements (sa réalisation et sa non-réalisation). Aussi utiliser les logarithmes en base 2 devient naturel, bien que cela ne soit pas une obligation.1Le sujet est complexe, mais on perçoit qu’une photo a une quantité d’information plus grande si sa définition augmente. On suppose que 1 octet transporte 8 shannons
Un événement rare procure une quantité d’information énorme : gagner au loto par exemple. Au contraire, un événement sûr donne une quantité nulle (Noël en décembre est un événement important mais dont la quantité \(i = 0\text{ Sh}\) suivant cette approche). Gagner ou perdre à un tirage à pile ou face est aussi une information.
L’importance de l’information (en termes affectifs, financiers ou autres) est laissée de côté. On parle ici uniquement de “quantités” que l’on pourra additionner. On verra par la suite que ces quantités pourront malheureusement diminuer dans un {canal} imparfait.
Source d’information
En fait, une information seule a peu d’utilité. Souvent il faut étudier toutes les informations issues d’une source, sur une longue période et de façon répétitive.
On définit la source d’information comme un mécanisme qui délivre de façon imprévisible un message parmi plusieurs. Elle peut être électronique (un microphone ou une caméra de télévision), mais aussi un livre, un paysage ou un championnat de football délivrant des scores (où on espère avec un minimum d’incertitude). Ainsi un son, une image, un mot dans un texte possède une quantité d’information.
Il est intéressant de définir l'{information moyenne} issue de la source. On l’appelle {entropie} et on la note \(H\).
Si la source \(X\) délivre \(n\) symboles différents \(x_1,\cdots x_n\), on définit l’entropie \(H(X)\) par :
\[H(X)=\sum_{k=1}^ni(x_k)p_k=-\sum_{k=1}^np_k \log_2 (p_k)\]
où \(p_k\) est la probabilité de l’événement \(k\).
Ainsi on peut déjà comparer des sources : une pièce de monnaie, un dé, un jeu de cartes sont différentes sources avec des entropies différentes. Mais on peut aussi comparer les quantités d’information de texte, de photo ou de son.

L’entropie est la moyenne pondérée par les probabilités d’apparition de toutes les informations possibles. En fait, elle peut aussi être vue sous différentes formes : la complexité de la source, le désordre, l’agitation ou la complexité des observations. En physique (thermodynamique et astrophysique), le même mot est employé sous des formes voisines .
L’entropie est la moyenne pondérée par les probabilités d’apparition de toutes les informations possibles. En fait, elle peut aussi être vue sous différentes formes : la complexité de la source, le désordre, l’agitation ou la complexité des observations. En physique (thermodynamique et astrophysique), le même mot est employé sous des formes voisines .
Canal d’information et perturbations
Définitions
Un canal est la totalité des moyens mis en œuvre à la transmission du message depuis la source à sa destination : l’auditeur, le spectateur, le lecteur ou une machine.
Dans la vie courante, rien ne vient gêner la lecture d’un tirage au sort, d’un livre ou d’une image. Mais pour Shannon, il s’agissait d’analyser des situations plus difficiles, par exemple les communications entre deux antennes radio éloignées l’une de l’autre. Ce que le récepteur entendait n’avait que trop peu à voir avec ce qui était émis par l’émetteur !
En tel cas, on dit que le canal est perturbé. Les perturbateurs sont de natures diverses. Ainsi pour les liaisons radio, il s’agit des bruits électroniques ou des brouilleurs. De nos jours, une liaison internet peut être perturbée par des saturations de serveur. Lorsque celui-ci est surchargé de travail (ou attaqué par un hackeur), il peut ralentir voire complètement arrêter de travailler.
Dans la suite de cet article on limitera nos canaux au simple passage de l’information depuis sa source à son destinataire.
On peut schématiser une liaison par le diagramme suivant :
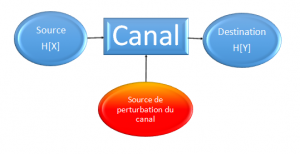
Figure 1 : Schéma d’un système de transmission
La notion d’information définie par Shannon est un peu différente de celle de la vie quotidienne.
La réalisation d’un événement parmi \(N\) possibles signifie que l’on obtient une {information}. Celle-ci sera d’autant plus grande que l’événement sera imprévisible. Par définition, on fixe :
\[i = \log_2\left( {1\over p}\right) = -\log_2 (p)\]
où \(p\in ]0,1]\) est la probabilité de cette réalisation. Cette {quantité d’information} \(i\) (positive puisque le nombre \(\log_2 (p)\) est négatif quelle que soit la probabilité traitée) est souvent exprimée en {shannon} (\(\text{Sh}\)) 2En réalité, Shannon utilisa le terme “bit”, contraction de “binary digit”. Ce terme s’étant généralisé, on préfère utiliser en théorie de l’information le terme “shannon”. On note que suivant la théorie de Shannon, on ne peut pas traiter moins de deux événements (sa réalisation et sa non-réalisation). Aussi utiliser les logarithmes en base 2 devient naturel, bien que cela ne soit pas une obligation.
A cause des perturbations, on peut se demander si la destination est identique ou ressemble suffisamment à la source. L’idée de Shannon est de comparer les différentes entropies \(H(X)\) et \(H(Y)\) (qui sont égales dans le cas idéal), puis de définir la {transinformation} \(I\) de la source \(X\) vers la destination \(Y\), notée \(I(X ; Y)\). En annexe on trouvera les bases de ce concept que l’on peut résumer à :
\[I(X;Y) = H(X) – H(X|Y).\]
\(H(X|Y)\) s’appelle l'{équivoque} : on connaît la sortie et on estime l’entrée. Par exemple, si je reçois la lettre \(A\), on estime (grâce à une précédente campagne de mesures) que je n’ai par exemple que \(99,9\%\) d’avoir \(A\) à la source. L’idéal est d’avoir l’équivoque nulle (0 Sh). Ici on a un défaut de \(0,001\) Sh. Les quantités d’informations sont positives, donc on a toujours \(I(X;Y) \leq H(X)\). L’équivoque \(H(X|Y)\) s’appuie sur les probabilités conditionnelles. On lit “entropie de \(X\) sachant \(Y\)”. Plus le bruit (perturbations ou défauts) sera grand, plus l’équivoque le sera aussi, et plus la transinformation sera réduite. La formule peut se traduire par :
Transinformation = Entropie de la source – Bruit du canal
Un canal parfait offre la relation suivante :
Transinformation d’un canal parfait = Entropie de la source
Un canal totalement bruité :
Transinformation d’un canal coupé = 0
Exemple de canaux d’informations
Parler de canaux d’information est banal dans les mondes informatique et télécom, mais ce concept est aussi universel que la notion de probabilité. Le tableau ci-dessous passe en revue quelques exemples, éloignés peut-être les uns des autres mais qui ont une similarité avec le schéma ci-dessus :
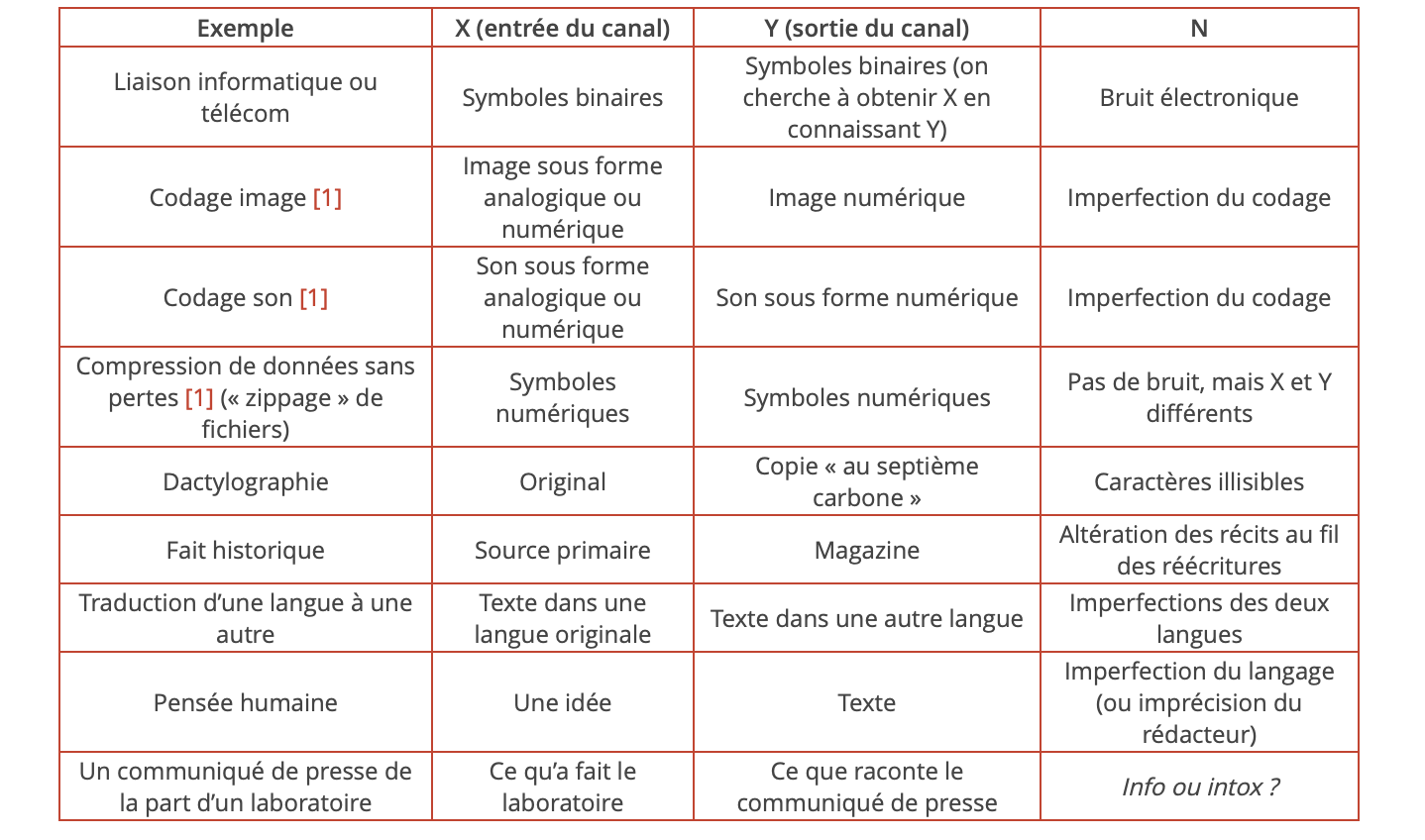
Table 1. Exemples de canaux d’information
Il n’y a pas de limite à ce tableau si chaque symbole de \(X\) et de \(Y\) a une probabilité d’apparition bien définie (ce qui complique considérablement l’étude des deux derniers exemples). Quant au perturbateur \(N\), il peut soit exister par exemple sous forme de bruit électronique, soit rester caché dans les imperfections d’un codage, d’un algorithme ou d’un protocole. On note que \(N\) peut être présent dans le canal (cas le plus classique), mais aussi dans la source (en compressant un peu trop une image photo par exemple). On peut appeler \(N\) tout ce qui réduit la transinformation \(I\). Il montre que le passage dans un canal est sujet à toute imperfection.
On peut ajouter que si vous voulez décrypter un message secret du FBI ou une écriture ancienne (au choix, le linéaire B crétois), vous utiliserez les mêmes bases : repérage des symboles utilisés, fréquences d’apparition, etc. et entropies !
Le dernier exemple du tableau s’éloigne sans doute de ce que les physiciens envisageaient et prêterait à sourire si les enjeux restaient modestes. Ainsi une banque cherche à savoir si le “teasing” d’un solliciteur est sincère et si elle peut prêter de l’argent pour développer un prototype. Vantardise ou escroquerie, un “bidonnage” fait par un entrepreneur est aussi une perte d’information (au sens de Shannon) vue de ceux qui sont abusés.
(Pour être complet, il faudrait parler codages, modulation, énergie. Le sujet est immense. L’article [1], Claude Shannon et la compression des données de Gabriel Peyré, développe le codage de source : avec le minimum de symboles transmettre la totalité (ou presque dans le cas d’images) des informations. Si le présent article analyse l’aspect “canal”, en [1] sont vus les codages d’images, de sons, de compressions sans pertes à la source.)
Exemple d’une analyse médicale
Dans une ville, une mystérieuse maladie tropicale frappe la population. Épouvanté, le maire décide de lancer une vaste politique de prévention. Il veut tester tous ses concitoyens. Un laboratoire propose un test rapide, pas cher, mais pas totalement parfait. Un dossier montrera les résultats sur une population témoin de \(10\;000\) testeurs. Le maire tente de se faire une idée. L’équipe médicale propose la modélisation suivante :
- Un patient X peut présenter deux états distincts : sain ou atteint de cette maladie tropicale ;
- Le test médical figure un canal d’information ;
- Et Y le résultat de ce test (positif ou négatif), on l’espère le plus proche possible de la réalité X.
Parmi les testeurs figurent \(100\) malades, dont \(99\) vus correctement par le test rapide. Mais \(200\) sont diagnostiqués positifs à tort. On met en ordre ces données dans la matrice du champ réuni “entrée-sortie” ou \([X, Y]\) :
\[[X,Y]=\pmatrix{9\;700&{\color{Red}{200}}\cr {\color{Red}1}&99}.\]
Cette notation matricielle montre \(X\) en lignes : on voit les \(9\;900\) (soit \(9\;700 + 200\)) personnes saines sur la première ligne et \(100\) personnes atteintes sur la seconde (soit \(1 +99\)). Y est lisible en colonnes et affirme que \(9\;701\) personnes sont saines (\(9\;700 + 1\)) et \(299\) sont atteintes (\(200 + 99\)).
Cette forme de matrice est universelle et s’appelle aussi {matrice de confusion} pour les réseaux neuronaux. En effet, si le laboratoire est un canal d’information, celui-ci n’est pas parfait. Déjà on peut voir que l’on s’écarte d’une matrice idéale où seuls les termes de la diagonale seraient non nulles :
\[[X,Y]_{idéal}=\pmatrix{9\;900&{\color{Green}0}\cr {\color{Green}0}&100}.\]
On peut alors bâtir une matrice de probabilité \(P(X,Y)\). C’est plutôt simple dans nombre de domaines, mais il y a toujours un doute en biologie. Ici il faut vérifier qu’en termes d’âge, sexe ou groupe sanguin l’échantillon soit représentatif de la population totale ciblée. Si on le suppose représentatif de toute la population, on obtiendra une estimation suffisante de la matrice des probabilités croisées entrée-sortie :
\[P([X,Y])=\pmatrix{0,97&0,02\cr 0,0001&0,0099}.\]
(La somme des probabilité d’une telle matrice vaut 1.) En appliquant les formules qu’on trouve en Annexe, on trouve :
- \(H(X, Y) = H(X) + H(Y|X) = H(Y) + H(X|Y) = 0,22\text{ Sh}\) ;
- \(H(X) = 0,08\text{ Sh}\) ;
- \(H(Y) = 0,19\text{ Sh}\) ;
- \(H(X|Y) = 0,03\text{ Sh}\) ;
- \(H(Y|X) = 0,14\text{ Sh}\) ;
et :
- \(I(X;Y) = H(X) + H(Y) – H(X, Y) = H(X) – H(X|Y) = H(Y) – H(Y|X)\)
- \(I(X;Y) = 0,05 \text{ Sh}\) .
On voit bien que \(I(X;Y) < H(X)\). La transinformation \(I(X; Y)\) est plus petite que \(H(X)\), à cause de deux défauts :
- La probabilité de détection \(P_D =99 / (99+1) = 99\%\), alors que l’idéal serait \(100\%\) ;
- La probabilité de faux positifs \(P_{FA}= 200 / (200+99) = 67\%\), alors que l’idéal serait \(0\%\).
On pourrait procéder à un second test de préférence avec un moyen différent pour améliorer les performances. Mais ce n’est pas toujours possible : le taux de faux positifs peut devenir problématique. Peu importe si votre alarme incendie vous dérange une ou deux fois dans l’année si vous êtes en sécurité. Mais ici, il se produit un phénomène étrange : les faux positifs sont plus nombreux que les vrais. Comment les médecins pourraient-ils rassurer les nombreux patients qui s’affoleraient pour rien ? Certains pourraient même de façon somatique développer des symptômes et devenir malades à cause d’un test pourtant inoffensif. Trop de faux positifs peuvent empêcher une politique de prévention, pourtant rapide et saine.
3 La transinformation diffèrent fortement suivant que le résultat est positif ou négatif.Si \(Y\) révèle une absence de contagion (on ne regarde que les \(9\;701\) cas concernés), le calcul ci-dessous montre que la transinformation \(I(X ; Y=0)\) est faible (\(0,01\) Sh) : d’un point de vue pratique, beaucoup de personnes seront dérangées pour rien.
Par contre si \(Y\) montre cette contagion (pour les \(299\) autres cas), la transinformation \(I(X ; Y=1)\) est importante (\(1,29\) Sh), car le test repère correctement les cas rares (malgré les fausses alarmes).
La transinformation totale \(I(X ; Y)\) est la moyenne pondérée de ces deux transinformations partielles \(I(X ; Y=0)\) et \(I(X ; Y=1)\).
- \(I(X ; Y=0) = 0,01\text{ Sh}\) ;
- \(I(X ; Y=1) = 1,29\text{ Sh}\) ;
- \(I(X ; Y) = P(Y=0) I(X ; Y=0) + P(Y=1) I(X;Y=1) = 0,01 +0,04 = 0,05\text{ Sh}\).
Différentes anecdotes
Dans les années 60, légende ou réalité, on racontait qu’un opérateur radar soviétique se demanda s’il voyait vraiment une attaque aérienne et s’il fallait lancer une riposte ; il s’agissait d’une fausse alerte due à des cigognes en trop grand nombre. Cette histoire montre que les faux positifs sont à prendre en considération.
En Indonésie, une fausse alarme volcanique pourrait déplacer à tort un demi-million d’habitants et provoquer une perte de confiance dans les futures décisions des autorités gouvernementales.
Ajoutons que l’Australie, en décembre 2020, renonça à développer un vaccin anti-covid qui créa trop de faux positifs au VIH.
Le choix n’est pas toujours simple, et le fait que \(I(X ; Y)\) soit plus faible que \(H(X)\) l’explique de façon quantitative.
Conclusion
Quelle que soit l’information, venant d’un processus physique, une machine ou un humain, et dont vous seriez destinataire, demandez-vous toujours “Par quel canal, fiable ou déformant, cette information m’est-elle parvenue ?”. Le “bruit” peut s’insérer partout en cette époque de “vérités alternatives” et de “fake news”, et avoir l’esprit critique devient vital.

Shannon faisant du monocycle et jonglant.
Plus pernicieux, si manquer un événement important est évidement problématique, une fausse alarme peut faire autant de mal.
La théorie de C. Shannon se prête bien aux transmissions électroniques, mais aussi à tout ce qui touche les probabilités. Les exemples dans la vie professionnelle ou privée sont nombreux. Elle permet d’analyser nombre de problèmes sous un angle nouveau, à l’aide d’outils comme les sources, les canaux d’information et leur transinformation. Voir les analyses médicales et les détecteurs incendie avec le même schéma, c’est bien une originalité qui aurait plu à Shannon !
Postérité
Dans sa carrière, Claude Shannon remporta une quinzaine de prix et devint membre d’une demi-douzaine de sociétés savantes. Bien que ses travaux ont des liens avec la physique, ils sont fortement basés sur les mathématiques et l’on affirme qu’il n’a pas eu de prix Nobel à cause de cela. En 1972 fut créé le prix Claude-Shannon dont il fut le premier lauréat. Il existe plusieurs théorèmes portant son nom (Nyquist-Shannon, Shannon-Hartley, etc.). Il en existe même un sur le jonglage !
Bibliographie
[1] «Claude Shannon et la compression des données» — Images des Mathématiques, CNRS, 2016.
[2] Shannon, C.E. et Weaver, W. {The mathematical Theory of communication}, University of Illinois, Urbana III, 1949.
[3] Spataru, A. {Fondements de la théorie de la transmission de l’information}, Presses polytechniques romandes, 1987, chapitres 1 à 4.
Post-scriptum
Je remercie chaleureusement Aziz El Kacimi pour ses conseils, sa lecture avisée et son soutien. Merci aussi à Philippe Colliard pour son travail de relecture et ses suggestions de retouche.



Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.