
Le vrai titre du trimestre RANDOM qui se tiendra à l’IHP du 5 janvier 2015 au 3 avril 2015 est « Disordered Systems, Random Spatial Processes and Some Applications ». Voici six bonnes raisons de ne pas y aller par hasard.

Pourquoi six bonnes raisons ? Car c’est autant que le nombre de lettres du mot RANDOM.
R comme RENCONTRE.
Avant tout, un trimestre à l’IHP c’est une, et même plusieurs rencontres. Les chercheurs se rencontrent, ils échangent de vive voix, et non plus seulement par mail ou par article interposé. Pour les doctorants et les plus jeunes chercheurs ce sera aussi l’occasion de rencontrer pour la première fois ceux dont ils ont si souvent vu les noms sur les livres ou les articles. Voir ces grands ténors de la discipline « en vrai » peut être un moment exceptionnel — parfois aussi un peu décevant — mais dans tous les cas, ce sont des rencontres dont on se souvient longtemps !
A comme ALÉATOIRE.
L’aléatoire et plus précisément les systèmes aléatoires vont être le sujet central de ce trimestre à l’IHP. Qu’est ce qu’un « système aléatoire » ? De façon très générale, un système est un ensemble de « particules » et l’aléatoire intervient alors soit dans l’état de ces particules, soit dans leur position spatiale, soit aussi dans leur nombre total (certaines peuvent « mourir » et d’autres peuvent « naître »). Donnons deux exemples simples de systèmes aléatoires.
Le premier exemple est celui de la percolation.

Les sites sont occupés (en noir) avec probabilité \(p=0,4\). On observe une multitude de petits amas.
On se place dans le plan, et chaque point du plan dont les coordonnées sont entières (positives ou négatives) est appelé un site. Chaque site est occupé avec probabilité \(p\) (un nombre entre \(0\) et \(1\)) ou vide avec probabilité \(1-p\), et ce indépendamment les uns des autres. On s’intéresse alors aux {amas} (appelés aussi {composantes connexes} en mathématiques) créés par les sites occupés : un amas est ici défini comme un ensemble de sites occupés tel qu’on peut joindre n’importe quel site de l’amas à n’importe quel autre en prenant un chemin de sites occupés (on est autorisé à se déplacer à gauche, à droite en haut ou en bas, mais pas en diagonale). Quelle est alors la taille moyenne de ces amas ? En existe-t-il un qui soit infini ? Même si le modèle de départ est simple, la réponse à ces questions est compliquée. Par exemple, on peut montrer qu’il existe une valeur critique de \(p\), appelée seuil de percolation et notée \(p_c\) à partir de laquelle il existe un amas infini (le système «percole»). Mais la valeur exacte de \(p_c\) n’est pas connue. Des méthodes numériques permettent de l’estimer : on a \(p_c\simeq 0,5927…\). La percolation sert en général à modéliser des phénomènes physiques, mais elle peut aussi être utilisée dans la modélisation de propagation d’épidémies, comme le montre Jacques Istas dans cet article.
Un deuxième exemple simple de système aléatoire est celui d’une particule qui se déplace sur \(\mathbb{Z}\), l’ensemble des entiers positifs ou négatifs.

Les sites sont ici occupés (en noir) avec une probabilité \(p=0,7\), qui est plus grande que dans l’exemple précédent. On observe qu’il y a essentiellement un seul « gros » amas. Le cas extrême serait celui où \(p=1\) et où les sites sont alors tous occupés.
Au temps \(0\) la particule est en \(0\) puis au temps \(1\) elle fait aléatoirement avec probabilité \(1/2\) un saut de \(-1\) ou un saut de \(+1\), et ainsi de suite suivant le même principe. On peut alors étudier la trajectoire de la particule en fonction du temps: quelle est sa position la plus éloignée de \(0\) ? Va-t-elle revenir en \(0\) ? Si oui, au bout de combien de temps ? etc. Ce modèle s’appelle une {marche aléatoire} sur \(\mathbb{Z}\), et sa limite (dans un sens qu’il faut définir précisément) est le fameux mouvement brownien. Le modèle peut aussi être rendu plus compliqué en mettant plusieurs particules qui n’ont pas le droit de se croiser, ou en faisant mourir des particules tout en faisant naitre de nouvelles, ou bien encore en se plaçant en dimension plus grande (sur \(\mathbb{Z}^2\) ou \(\mathbb{Z}^3\) par exemple).
Un tel modèle a de nombreuses applications en physique, mais aussi en finance par exemple.
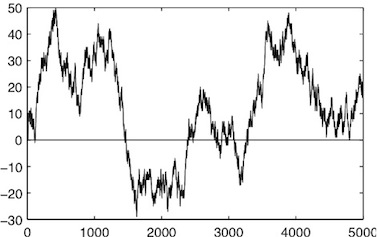
Exemple de trajectoire d’une particule entre les temps \(0\)et \(5000\). On observe beaucoup de petites fluctuations mais aussi des fluctuations à plus grande échelle.
N comme NOMBREUX.
Dans ce trimestre, de nombreux événements sont prévus : il y a d’abord une école d’hiver introductive au CIRM (c’est maintenant une habitude pour les trimestres à l’IHP, voir à ce sujet l’article de Pierre Pansu sur le trimestre précédent), une douzaine de mini-cours, trois workshops internationaux d’une semaine chacun. Ces événements sont plutôt destinés aux spécialistes, mais il y a aussi trois exposés destinés au grand public. De nombreux participants sont également attendus : il y a déjà plus de 200 inscrits à ce trimestre, et ce nombre va certainement encore augmenter. Parmi eux, des doctorants et des chercheurs de tous âges, de toutes nationalités et venant de différentes disciplines : mathématiques, physique, informatique, mais aussi économie ou sciences sociales. Parmi la longue liste de participants, signalons en particulier la présence de Joël Lebowitz qui vient de recevoir la grande médaille 2014 de l’Académie des sciences et qui, comme le mentionne le communiqué de presse, incarne « l’humanisme et l’universalité de la science ». Signalons aussi la présence d’Ivan Corwin, titulaire d’une chaire Poincaré, et dont Images des mathématiques a déjà parlé dans cet article.
L’organisation d’un tel trimestre demande évidemment du temps. Les organisateurs (Jean-Philippe Bouchaud (École polytechnique Paris), Pierluigi Contucci (Alma Mater Studiorum Università di Bologna), Cristian Giardinà (Università degli studi di Modena e Reggio Emilia), Pierre Nolin (ETH Zürich), Vladas Sidoravicius (IMPA Rio de Janeiro) et Vincent Vargas (École normale supérieure Paris)) m’ont confié qu’ils avaient commencé à y travailler il y a deux ans et que heureusement ils sont aidés dans leur travail d’organisateurs par une équipe exceptionnelle à l’IHP !
Toutes les informations pratiques sur le programme, le lieu et les inscriptions se trouvent ici.
D comme DÉSORDONNÉ.
Le titre du trimestre m’interpelle : c’est quoi un « disordered system » ? Est-ce que c’est pareil qu’un « random system » (système aléatoire) ? Et bien non ! Les systèmes désordonnés sont des systèmes aléatoires ayant un comportement particulier. Et tous les systèmes aléatoires ne sont pas désordonnés. Etre « désordonné » est ici un terme de physique statistique qui désigne un système où la corrélation entre particules éloignées est très petite. Un des exemples les plus simples de système désordonné est l’exemple d’un alliage métallique appelé verre de spin. Dans un tel système, même à l’équilibre, les spins (représentés par des petits vecteurs dirigés vers le haut ou vers le bas) ne s’alignent pas tous dans le même sens et il y a absence de corrélation entre des atomes éloignés. A l’inverse, dans ce qu’on appelle un solide ferromagnétique, à l’équilibre, les spins s’alignent tous dans le même sens. La corrélation entre spins distants est très grande, et on parle alors d’un système ordonné.
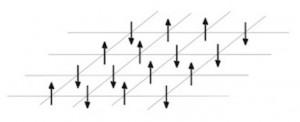
Représentation schématique d’un système de spin.
O comme OISEAUX.
Qu’est-ce que les oiseaux viennent faire ici ? Et bien, comme beaucoup d’autres, ils viennent se faire modéliser ! Plus précisément, c’est leur comportement collectif qui est ici objet de modélisation. Les nuées d’oiseaux tels que les étourneaux forment des ensembles fascinants et il est fascinant aussi de chercher à comprendre comment le comportement global de la nuée émerge à partir des comportements individuels et des interactions locales entre les oiseaux. Grâce à l’enregistrement de données précises, les chercheurs de 1M. Ballerini, N. Cabibbo, R. Candelier, A. Cavagna, E. Cisbani, I. Giardina, V. Lecomte, A. Orlandi, G. Parisi, A. Procaccini, M. Viale, V. Zdravkovic, “Interaction ruling animal collective behavior depends on topological rather than metric distance : evidence from a field study”, Proceedings of the National Acadamy of Sciences U.S.A., vol.105(4), p.1232-1237, January 29, 2008. ont pu montrer que les interactions qui interviennent dans le comportement global de la nuée dépendent de la distance « de voisinage » et non pas de la distance « métrique ». En d’autres termes : un oiseau interagit avec un nombre fixe de ses voisins (de 6 à 7 précisément) quelle que soit leur distance plutôt qu’avec tous ses voisins à distance donnée. Un telle interaction est indispensable pour maintenir la cohésion spatiale de la nuée malgré les perturbations externes. Vous voulez en savoir plus ? Rendez-vous à la conférence grand public d’Andrea Cavagna « Le septième étourneau : les merveilles du comportement animal collectif » 2« The seventh Starling : the Wonders of Collective Animal Behaviour » le 19 février 2015 à l’IHP ! Comprendre les liens entre comportements individuels et collectifs est un défi passionnant pour les mathématiques comme l’a déjà expliqué Pierre Degond dans un article sur le site d’Images des Mathématiques.

Une nuée d’étourneaux.
M comme MATHÉMATIQUES.
Bien sûr, les mathématiques sont au cœur de ce trimestre, mais elles ne sont pas seules comme en témoigne la grande diversité des applications et des problèmes abordés. Cette diversité est d’ailleurs à l’origine du trimestre RANDOM, comme en témoigne Pierluigi Contucci, un des organisateurs du trimestre : « Nous observons de plus en plus souvent des physiciens et des mathématiciens travaillant sur des problèmes issus des sciences sociales, de l’économie ou des sciences du vivant. L’idée de ce trimestre est de créer l’occasion de discuter de sujets sur les systèmes complexes avec l’approche rigoureuse des sciences dures. » (traduction de 3We are witnessing, increasingly often, physicists and mathematicians working on problems that come from social, economic and life sciences. The idea of the trimester came to create an occasion to discuss topics on complex systems with the rigorous approach of the hard sciences.).
Mais les systèmes aléatoires ne trouvent pas seulement des applications à des domaines extérieurs aux mathématiques. Ainsi, pour Cristian Giardinà, un autre organisateur du trimestre, « des avancées récentes trouvent aussi leur application dans d’autres branches des mathématiques telles que l’étude des équations aux dérivées partielles stochastiques non linéaires. Il y a même une conjecture — comme l’expliquera Charles Newman (professeur à NYU) — selon laquelle la théorie des probabilités pourrait aider à résoudre l’hypothèse de Riemann, la plus fascinante des conjectures mathématiques. » (traduction de 4These recent breakthroughs find also their application in other areas of mathematics, such as the study of non-linear stochastic partial differential equations. There is even a conjecture — as will be explained in the lectures of NYU professor Charles Newman — that probability theory might help in the solution of the Riemann Hypothesis, the most fascinating conjecture of mathematics.).
Pour finir, on peut tout à fait reprendre une phrase du rapport de prospective publié le 21 octobre 2014 par le conseil scientifique de l’Institut national des sciences mathématiques et de leurs interactions (INSMI) du CNRS : « En conclusion, les mathématiques deviennent de plus en plus multiformes et continuent à s’ouvrir aux autres disciplines et aux applications. » L’intégralité du rapport, par ailleurs fort instructif, se trouve ici.



11h17
J’ai un petit problème avec la couleur de la piste de cet article (rouge = j’ai un niveau de Terminale S d’aujourd’hui) et son titre. L’article parle des bonnes raisons d’aller à l’IHP pour ce trimestre, il me semble que si je suis en Terminale S, l’unique bonne raison (à comparer aux six évoqués dans le titre) est d’aller voir les conférences publiques (on peut alors dire qu’il y a trois bonnes raisons, vu le nombre des conférences).
Après je suis tout à fait d’accord pour dire qu’il y a (au moins) 6 bonnes raisons de parler de cette conférence. Le titre associé à la couleur de l’article laisse penser que les lycéens sont les bienvenus.
Bien sûr, je pinaille. Mais je trouve un petit peu dommage qu’un article, qui est par ailleurs accessible par son contenu, laisse penser (par son titre surtout) qu’on puisse aller durant tout le trimestre voir ce qui se passe là-bas en non-spécialiste et qu’au contraire les conférences grand public ne soient pas plus mises en valeur.
Merci quand même pour cette présentation du trimestre fort intéressante.