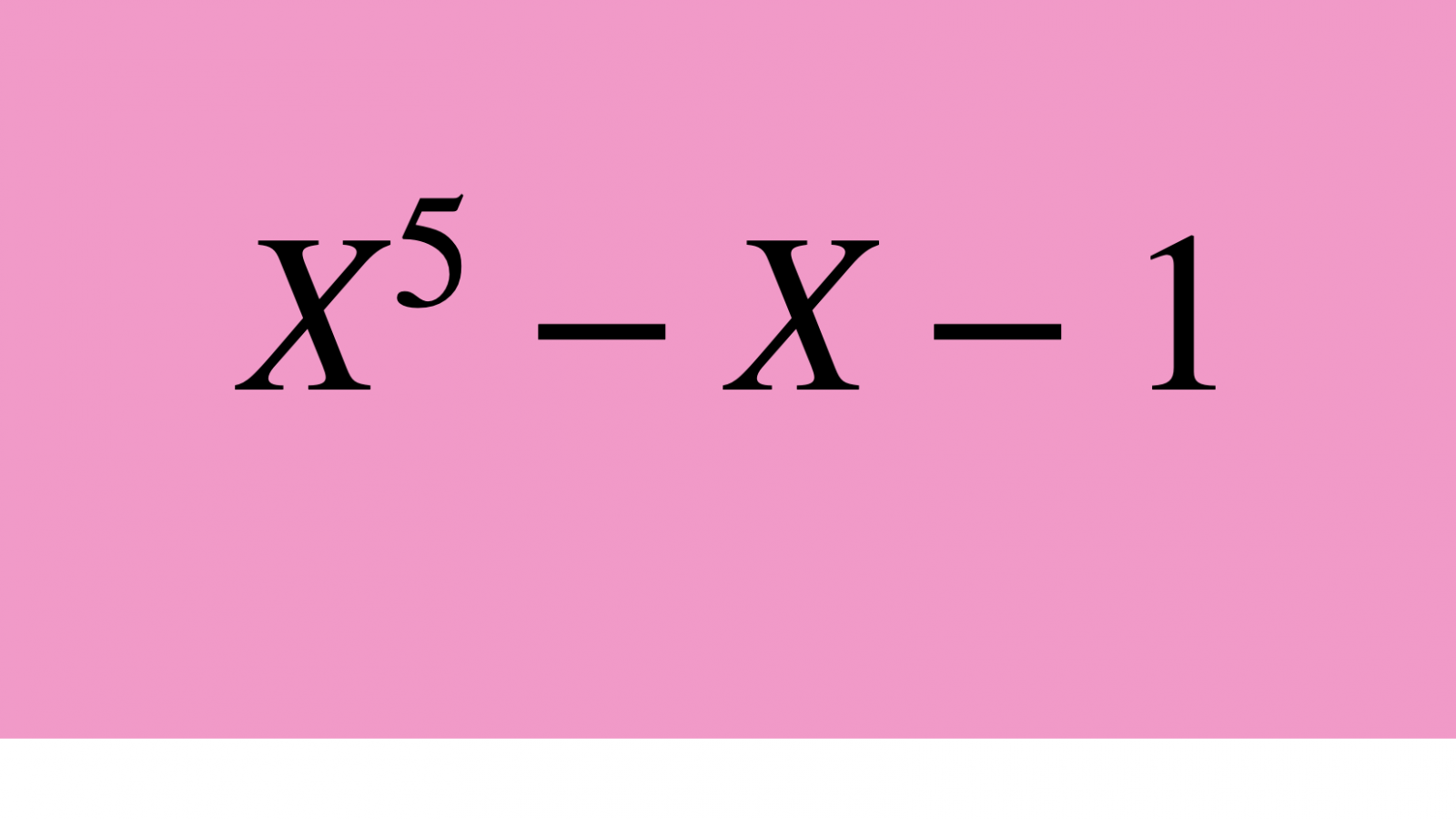
Soit G un groupe
Un groupe est un objet mathématique abstrait. Nous allons voir ici que c’est surtout une notion utile, naturelle, utilisée en particulier par Evariste Galois, dont on fête aujourd’hui le bicentenaire. Bien que Galois n’ait pas donné la définition de groupe, gageons qu’il ne démentirait pas la puissance du formalisme en mathématiques.
Quelques exemples de groupes
Comme Monsieur Jourdain fait de la prose sans le savoir, vous tous, lecteurs, connaissez déjà quelques groupes. Un groupe est un ensemble muni d’une opération ayant certaines propriétés. Par exemple, quand on ajoute ou retranche deux entiers relatifs, on manipule une structure de groupe sur l’ensemble \(\mathbf{Z}\). Quand on multiplie ou divise des fractions rationnelles non nulles, on manipule une structure de groupe sur l’ensemble \(\mathbf{Q}\backslash \{0\}\). Mais attention, quand on additionne deux entiers naturels, on ne trouve pas un groupe parce que l’opposé d’un entier naturel n’est pas un entier naturel mais un entier relatif 9 sauf pour \(n=0\) bien entendu.. Pour tester si un ensemble muni d’une opération est un groupe, on pourra se reporter à la définition ci-dessous.
Mais voici un autre groupe, inspiré par le jeu de Mastermind, dont on modifie un peu les règles.
.
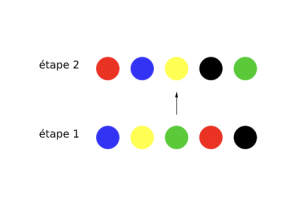
Dans cette version modifiée, le joueur B doit deviner comment \(5\) pions de \(5\) couleurs distinctes sont disposés par le joueur A. À chaque coup, le joueur A indique au joueur B le nombre de couleurs bien placées. Combien y-a-t-il de possibilités de combinaisons ? \(5\) pour la première case (celle de gauche), \(4\) pour la deuxième, …, soit \(5!=120\) possibilités. Le but du jeu est de trouver la combinaison choisie par A, en permutant les couleurs de départ. Voici, à gauche, un exemple de deux premiers coups de B, en supposant que la première combinaison proposée par B ne contienne aucune couleur bien placée.
La permutation effectuée par le joueur B envoie le bleu sur le rouge, le jaune sur le bleu, le vert sur le jaune, le rouge sur le noir. Il n’y a plus le choix pour le noir qui doit être envoyé sur le vert.
Faisons quatre remarques:
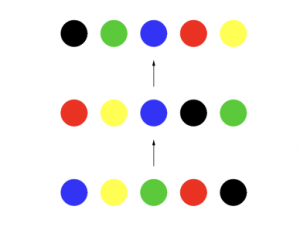
- On peut enchaîner (on dira composer) les permutations: si le joueur B tente une combinaison, puis une nouvelle en permutant cette nouvelle disposition, il obtient aussi une permutation de la disposition de départ. Par exemple, s’il procède à l’enchaînement suivant,
1
il aurait gagné un coup en effectuant directement celui-ci.
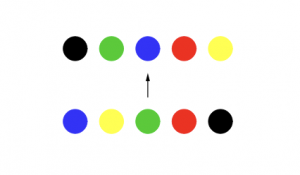
2
- On peut ne rien changer à la disposition de départ en ne permutant rien du tout. Cette permutation, pas très utile pour le jeu, est la permutation identique. La voici.
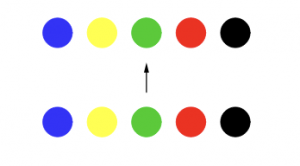
3
- Si on a permuté une disposition de couleurs, on peut toujours revenir en arrière, en permutant les couleurs de façon à revenir à la disposition initiale. On dit que toute permutation a un inverse. Voici un exemple
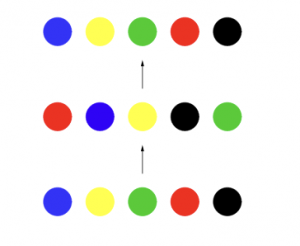
4
- Effectuons deux permutations \(p\), \(q\), suivies de \(r\) une troisième permutation. On trouvela même chose que si l’on effectue d’abord la première \(p\), suivie de la composée de \(r\) avec \(q\).
Ces quatre propriétés sont exactement les axiomes d’un groupe. Celui qui intervient ici
est le groupe des permutations d’un ensemble à \(5\) éléments.
On trouve d’autres groupes de permutation dans la nature et dans d’autres jeux comme le taquin.
Permutations et équations algébriques
Au début du 19e siècle, on connaissait des formules pour résoudre des équations comme \( ax^2+bx+c=0.\) Voici une telle formule:
\[x=\frac{-b+/-\sqrt{b^2-4ac}}{2a}.\]
Pour une équation, du 3e degré, on disposait aussi des formules de Cardan. Par exemple,
pour l’équation \( x^3+3px+2q=0\), on trouve une solution
\[ x=({\sqrt{q^2+p^3}-q})^{1/3} + ({\sqrt{q^2+p^3}+q})^{1/3}.\] Les deux autres solutions sont aussi données par de telles formules. Il existe aussi une méthode avec des formules, due à Ferrari, pour résoudre les équations de degré \(4\). Notons qu’on s’intéresse ici aux solutions en nombres complexes de ces équations, c’est-à-dire qu’on adjoint aux nombres classiques les nombres dits imaginaires, de sorte qu’une équation de degré donné égal à \(d\) possède en général \(d\) solutions distinctes.
La question, posée depuis (au moins) Lagrange, était: y a-t-il toujours des formules pour résoudre des équations algébriques ? Il se trouve que certaines opérations algébriques liées à l’équation permutent les solutions de l’équation entre elles 10Ces opérations ne sont pas magiques mais un peu trop difficiles à expliquer ici.. En général, si on prend une équation de degré \(5\), on associe par cette méthode le groupe des permutations des \(5\) solutions de l’équation, le même groupe que celui avec lequel a joué le joueur de Mastermind. C’est le cas par exemple pour l’équation
\[X^5-X-1=0.\] Voici dessinées les solutions en nombres complexes de cette équation, en noir, on a l’unique solution réelle.

.
Pour cette équation, permuter les solutions de cette équation revient à considérer le groupe qui lui est associé. Ce procédé est même très complet. Il faut y penser comme un dictionnaire, un peu difficile à établir explicitement, mais un dictionnaire quand même, entre les équations d’une part et les groupes d’autre part. Encore mieux: le fait de savoir résoudre une équation par des formules peut se lire sur ce groupe, cet ensemble abstrait associé à l’équation, sans qu’on ait besoin de calculer explicitement les formules donnant les solutions. Si tel est le cas, si l’équation est résoluble par des formules, alors le groupe qui lui est
associé dans le dictionnaire vérifie une propriété algébrique, concrète, qu’on appelle « être résoluble »11 terminologie bien entendu liée au contexte des équations algébriques.. Ainsi, quand je prends une équation, il me suffit en théorie de consulter mon dictionnaire, pour savoir si je peux résoudre cette équation par des formules algébriques. À condition que je sache à quel type de groupe j’ai affaire, résoluble ou pas.
Prenons une équation de degré \(2\), qui a deux solutions distinctes. le groupe qui lui est associé est l’ensemble des permutations des deux solutions \(x_1\) et \(x_2\). Ce groupe a deux éléments, la permutation identité qui envoie \(x_1\) sur \(x_1\) et \(x_2\) sur \(x_2\) et celle qui échange \(x_1\) et \(x_2\) (\(x_1\) est envoyé sur \(x_2\) et \(x_2\) sur \(x_1\)). Ce groupe à deux éléments est résoluble et c’est pour cette raison qu’on dispose d’une formule pour résoudre les équations de degré \(2\).
Revenons donc à notre équation de degré \(5\), \(X^5-X-1=0\). Le groupe qui lui est associé dans le dictionnaire est le groupe des permutations à \(5\) éléments. Galois a démontré que ce groupe n’est pas résoluble, de sorte qu’on ne peut pas résoudre cette équation par des formules.
Et maintenant …
La définition d'un groupe
Soit \(G\) un ensemble muni d’une loi de composition interne notée \(*\)12une opération qui, à deux éléments de \(G\) associe un élément de \(G\). On dit que \(G\) est un groupe si:
- il existe \(e\) dans \(G\) tel que pour tout \(x\) de \(G\), \(x*e=e*x=x\),
- pour tout élément \(x\) de \(G\), il existe un élément \(x^{-1}\) de \(G\), tel que
\(x*x^{-1}=x^{-1}*x=e\), 13\(x^{-1}\) est unique et est l’inverse de \(x\). - la loi \(*\) est associative, i.e. pour tous \(x,y,z\) dans \(G\),\[(x*y)*z=x*(y*z).\]Attention aux notations: pour voir que \(\mathbf{Z}\) est un groupe pour l’addition, il faut poser \(x^{-1}=-x\). Pour les permutations, la loi considérée est la composition des permutations.
Conclusion
L’intérêt d’une définition abstraite d’un groupe, c’est qu’elle s’applique à beaucoup de situations, de contextes différents. Ainsi, à chaque mathématicien ses groupes favoris, comme ici. 14qui ne sont pas forcément de Galois !.
Le travail de Galois est prodigieux à plus d’un titre. D’abord il a résolu un problème important. Ensuite, l’idée qu’il y ait un dictionnaire entre deux mondes mathématiques a priori différents 15 dont l’un, celui des groupes, n’avait jamais vraiment été étudié !, fut aussi à la fois novatrice, féconde et profonde. Une partie du travail de mathématicien consiste souvent, pour résoudre un problème, à établir et à construire de tels dictionnaires entre différents objets mathématiques.
Pour les conséquences du travail de Galois pour les mathématiques du 20e et du 21e siècle, on pourra consulter le très bon article d’Antoine Chambert-Loir 16Galois et les corps finis, Pour la Science, n° 408, octobre 2011..
Et il y a aussi Evariste Galois, le mathématicien engagé, qui paya son engagement politique par un séjour en prison.
Post-scriptum
Je remercie Rutger Noot pour sa lecture attentive, Adriano Marmora pour avoir déniché le polynôme \(X^5-X-1\), ainsi que M. Roux pour sa remarque sur l’équation de degré \(2\) que j’ai ajoutée au texte.
Les calculs et dessins pour ce texte ont été effectués à l’aide des logiciels libres GeoGebra et Sage.