A-t-on vraiment banni des manuels une preuve de géométrie élémentaire des triangles à cause de la subtilité du concept d’identité ?
Faut-il ou non présenter tôt aux enfants des raisonnements subtils, obligeant à un effort d’abstraction ou allant à l’encontre des habitudes de pensée ? Il s’agit probablement là d’une question au sujet de laquelle on se disputera aussi longtemps que l’humanité existera. Mais il est bon de pouvoir se disputer autour d’exemples concrets. En voici un que j’ai trouvé surprenant, raconté par Mark Kac 6Il s’agit de ma traduction d’un extrait de l’article « Will computers replace humans ? » de Kac, paru initialement dans le livre « The greatest adventure », édité par Eugene H. Kone et Helen J. Jordan, Rockefeller Univ. Press, New York, 1974. Cet article a été repris dans le livre d’essais sur les maths, les sciences et la philosophie « Discrete thoughts » de Mark Kac, Gian-Carlo Rota et Jacob T. Schwartz, seconde édition, Birkhäuser, Basel, 1992.:
Il pourrait sembler que l’ordinateur est entièrement dépendant de l’homme qui lui donne des instructions. «Âneries en entrée, âneries en sortie» est la manière méprisante de décrire parfois son manque total d’initiatives ou d’inventivité. Mais cette vision n’est pas entièrement juste, et l’ordinateur peut «enseigner» à ses maîtres des choses qu’ils ne connaissaient pas. Pour illustrer ce point je raconterai une histoire qui, tout en étant partiellement apocryphe, est entièrement plausible.
Il y a quelque temps, des tentatives furent faites pour apprendre à l’ordinateur à prouver des théorèmes de géométrie plane. Pour cela, en plus de lui donner des axiomes et des règles de déduction logique, il a fallu clairement lui fournir une «stratégie». Celle-ci était simple et consistait en l’unique commandement : «Cherche des triangles congruents.»7NDT : Rappelons que deux figures du plan sont dites {congruentes} si elles ont même forme et même taille. Pourquoi ne pas dire simplement qu’elles sont {égales} ? Afin de réserver ce terme à l'{identité} des deux figures, c’est-à-dire à la forme la plus forte possible de congruence. Mais on verra ici que l’identité est une notion subtile …
Étant donné un théorème à prouver, l’ordinateur considèrerait toutes les paires de triangles et, en retournant aux hypothèses, il chercherait à décider lesquels sont congruents. Si une paire de triangles congruents a été trouvée, alors toutes les conséquences de cette découverte seraient tirées et comparées avec ce qui doit être démontré. […] Si aucune conclusion obtenue de la sorte ne s’adapte à celle désirée, ou s’il n’y a pas de paire de triangles congruents, alors on instruisait l’ordinateur à tracer toutes les perpendiculaires possibles, toutes les bissectrices et les médianes, et à reprendre ensuite la recherche des triangles congruents.
Eh bien, voici ce qui arriva lorsque l’on demanda à l’ordinateur de prouver que, étant donné un triangle isocèle avec \(AC=BC\), les angles \(A\) et \(B\) sont alors eux aussi égaux [\(\angle A = \angle B\)].
Les auteurs du programme s’attendaient à ce que l’ordinateur, après une brève contemplation du triangle solitaire \(ABC\), décide de mener la hauteur \(CD\) et, de la congruence des triangles rectangles \(ADC\) et \(BDC\), conclue que \(\angle A = \angle B\).
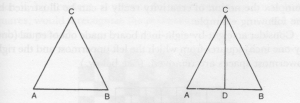
isocèle
Mais l’ordinateur les a bernés ! Il a donné une preuve beaucoup plus jolie et plus sophistiquée. Il a simplement «remarqué» que les triangles \(ABC\) et \(BAC\) (!) sont congruents et déduisit la conclusion désirée de cette manière.
Avant que quiconque bondisse, je me hâte de préciser que cette preuve n’est pas nouvelle. En fait, elle est très ancienne et a été donnée pour la première fois par Pappus au cinquième siècle après Jésus-Christ. Elle a été reproduite dans la plupart des textes de géométrie jusque vers la fin du XIX-ème siècle, lorsque l’on décida qu’elle était trop difficile à comprendre pour les jeunes humains.
La raison pour laquelle la preuve est difficile est que cela est contre nature de considérer \(ABC\) et \(BAC\) comme étant des triangles {différents}, même s’ils sont représentés par le même dessin 8NDT : Ici la manière d’associer les sommets est essentielle. Pour cette raison, lorsque l’on a choisi un ordre d’écriture pour les sommets du premier triangle, il est indispensable d’écrire correctement l’ordre des sommets du deuxième triangle. Dans notre cas, les triangles \(ABC\) et \(BAC\) sont congruents parce que les paires de côtés qui se correspondent dans ces deux écritures, c’est-à-dire \((AB, BA)\), \((BC, AC)\), \((AC, BC)\) ont à chaque fois la même longueur. Les angles aux sommets correspondant à la première lettre de chacune des deux suites de trois lettres sont donc égaux. On obtient bien \(\angle A = \angle B\)..
Je vois là une subtilité liée à la notion d’identité. En effet, la figure semble ne représenter qu’un seul objet, un triangle, et un objet est identique à lui-même. Oui, mais il peut être identique à lui-même de plusieurs manières ! Si cela se produit, on dit que cet objet admet des symétries.
Étudier les symétries des objets est primordial non seulement en mathématiques, mais en sciences en général. Un vaste domaine des mathématiques, la théorie des groupes 9Plusieurs articles d’IDM la concernent, par exemple La ticmatéma ou la mathématique du verlan de Sylvain Barré, Soit G un groupe de Christine Huyghe, Mon groupe préféré, \(PSL_2(\mathbb{Z})\) de Marie Lhuissier, De l’ambiguïté des puzzles aux idées de Galois de Xavier Caruso et Bruno Teheux, Ornements et cristaux, pavages et groupes de Pierre de la Harpe, Les ensembles limites de groupes kleinéens en 3D de Jos Leys ou bien Un peu de géométrie des groupes de Gilbert Levitt., traite des symétries des objets de la pensée de toutes les espèces imaginables. Afin d’être préparé psychologiquement à cette théorie, il peut être bon de se confronter de temps en temps à des phénomènes ou à des raisonnements faisant jouer un rôle aux symétries.
La preuve racontée par Mark Kac, passant par la constatation directe que le triangle \(ABC\) est congruent au triangle \(BAC\), constitue un tel raisonnement. Ce raisonnement est-il encore jugé « trop difficile pour les jeunes humains » ? Ou bien pourrait-il désormais refaire son apparition dans les manuels, à côté de la preuve plus conventionnelle passant par la construction du segment supplémentaire \(CD\)10Celui-ci n’a pas à être une hauteur. On peut tout aussi bien considérer la médiane ou la bissectrice. À chaque fois, on déduit que les triangles \(ADC\) et \(BDC\) sont congruents à partir d’un critère différent : soit par les égalités des trois paires de côtés correspondants, soit par celle de deux de ces paires, et de la paire d’angles formés par ces côtés.
Quelqu’un saurait-il retrouver des comptes-rendus de discussions pédagogiques des alentours de l’année 1900, expliquant les arguments utilisés pour éliminer cette preuve des manuels ? En tout cas, on a loupé ainsi une magnifique occasion de permettre aux enfants de réfléchir aux subtilités du concept d’identité.
Plus généralement, pourquoi les manuels ne contiendraient-ils pas des choses pour tous les goûts, un tronc commun ainsi que des échappées plus subtiles et passionnantes pour ceux qui se découvrent une curiosité spéciale pour la matière concernée ? Curiosité qu’il est bon non seulement d’éveiller, mais aussi d’entretenir, afin de permettre à chacun de découvrir les subtilités de son identité.
ÉCRIT PAR
Patrick Popescu-Pampu
Professeur - Université de Lille
10h19
Les deux preuves sont-elles si différentes ? Autrement dit, il faut pour la preuve « de l’ordinateur » prouver que les deux triangles ABC et BAC sont congruents, ce qui revient (plus ou moins) à montrer que le triangle admet une symétrie dont l’axe est… CD justement !
11h00
C’est exactement ce que je me suis dit en lisant. Et pire encore, utiliser la symétrie axiale pour démontrer la symétrie entre ABC et BAC est plus long que simplement démontrer la symétrie entre ABD et ACD puisqu’on montre à la fois ∠A=∠B et ∠B=∠A !
Mais, après réflexion, je me suis dit que peut-être l’auteur n’était pas si bête, et suggérait d’utiliser le théorème de congruence des triangles ayant même longueurs de côtés deux à deux, sans jamais faire appel explicitement à une quelconque symétrie.
La démonstration fait alors une ligne, mais utilise un théorème puissant. Ce qui est intéressant, c’est que même en utilisant la symétrie axiale, pour justifier que ABD et ACD sont effectivement symétriques, le plus simple est d’utiliser ce théorème de congruence.
La grande question finalement, c’est comment un résultat si naturel et puissant a pu se faire évincer des programmes !
Répondre à ce message
10h34
Merci pour cette jolie histoire !
Les programmes de vérification automatique de preuve apporteront peut-être aussi des idées et pas seulement un niveau de confiance plus élevé dans les résultats.