La courbure d’une courbe donne une mesure de la non-linéarité de cette courbe, tandis que la déviation (notion étudiée par Carnot en 1803 et étudiée et nommée ainsi par Transon en 1841) donne, quand à elle, la non-circularité d’une telle courbe. Si la notion de courbure est très connue et « omniprésente » dans la littérature, celle de déviation demeure, malheureusement, presque inconnue, inexploitée et inexplorée.
Ce billet essaie donc de jeter un peu de lumière sur cette notion si intéressante mais inexistante dans les programmes qui traitent des courbes planes.
Le concept de la déviation en un point pour une courbe étant en relation étroite avec celui de (rayon de) courbure en ce point, il ne sera pas sans intérêt de rappeler, même brièvement, la notion de courbure pour une courbe plane.
La courbure d’une courbe plane en un point
Soit \(\mathscr{C}\) une courbe plane définie par le paramétrage
\[f:I \to {{\bf R^2}},t \mapsto f(t)\] où \[f(t) = x(t)\overrightarrow i + y(t)\overrightarrow j.\]
On suppose que \(f\) est continûment différentiable jusqu’à un ordre suffisant et on pose \[f'(t)=(x'(t),y'(t)), f^{\prime \prime}(t)=(x^{\prime \prime}(t), y^{\prime \prime}(t)), …\]
Un point \(M_{0}=f(t_{0})\) de \(\mathscr{C}\) est dit régulier ou ordinaire si \(f'({t_0}) \ne 0\) (sinon il est dit singulier ou stationnaire). Si on a \(f'({t}) \ne 0\), pour tout \(t\) de \(I\), la courbe \(\mathscr{C}\) est dite régulière. (D’une façon générale, soit \(\mathscr{C}\) une courbe plane paramétrée d’un espace affine de dimension finie, de classe \({C^k}\). Soit \({M_0} = f({t_0})\) un point de \(\mathscr{C}\) ; on dit que \({M_0}\) est régulier à l’ordre \(p\), \((1 \le p \le k)\), si le rang de la famille \({\left( {{f^{(\lambda )}}({t_0})} \right)_{1 \le \lambda \le p}}\) est égal à \(p\), c’est-à-dire si les vecteurs \(f'({t_0}),f”({t_0}),…,{f^{(p)}}({t_0})\) sont linéairement indépendants. Si tous les points de \(\mathscr{C}\) sont réguliers à l’ordre \(p\), on dit que \(\mathscr{C}\) est régulière à l’ordre \(p\).))
En un point régulier \(M_{0}=f(t_{0})\) la courbe admet une tangente dirigée par le vecteur \(f'(t_{0})\) ; c’est la droite affine définie par le paramétrage
\[t \mapsto {M_0} + tf'({t_0}), t\in{\bf R}.\]
La tangente en \(M_0\) est la limite d’une sécante \((M_0M)\) lorsque le point \(M\) tend vers \(M_0\) en restant sur la courbe.
Notons aussi que le paramétrage \(f\) est dit normal si \(\left\| {f'(t)} \right\| = 1,\forall t \in I\). Dans ce cas l’abscisse curviligne du point \(M\) de paramètre \(t\), définie par le nombre (Ce nombre est bien défini ; c’est la valeur en \(t\) de la primitive de la fonction continue \(\xi \mapsto \varepsilon \left\| {f'(\xi )} \right\|\), qui s’annule en \({t_0}\).)
\[s = \lambda (t) = \varepsilon \int_{{t_0}}^t {\left\| {f'(\xi )} \right\|} d\xi \]
avec \(\varepsilon\) égal à \(1\) si le sens des \(t\) croissants est celui des \(s\) croissants, et à \(-1\) si le sens des \(t\) croissants est celui des \(s\) décroissants, égale \(\varepsilon(t-t_{0})\). Le point \(M_{0}\) de paramètre \(t_{0}\) est l’origine des abscisses curvilignes. Le paramètre est donc l’abscisse curviligne ; on dit alors que la courbe est définie par abscisse curviligne ou par la longueur d’arc.
Si la courbe \(\mathscr{C}\) est régulière, alors
\[{\left( {\mathop \lambda \limits^{ – 1} } \right)^\prime }(s) = \frac{\varepsilon }{{\left\| {f'(t)} \right\|}},\]
et il est aisé de vérifier que le paramétrage \(g = f \circ \mathop \lambda \limits^{ – 1} \) est normal. (En effet, on a \(\left\| {g'(s)} \right\| = \left\| {f’\left( {\mathop \lambda \limits^{ – 1} (s)} \right){{\left( {\mathop \lambda \limits^{ – 1} } \right)}^\prime }(s)} \right\| = \left\| {f’\left( t \right)\frac{\varepsilon }{{\left\| {f'(t)} \right\|}}} \right\| = 1\).)
On suppose la courbe \(\mathscr{C}\) orientée (intuitivement, par le choix d’un sens de parcours sur elle (Formellement, deux paramétrages définissent la même orientation lorsque les vecteurs dérivés sont positivement proportionnels ; on définit ainsi une relation d’équivalence sur l’ensemble des paramétrages d’une courbe, et on dispose de deux classes d’équivalence distinctes, appelées orientations. Si \(t \mapsto f(t)\) est un paramétrage de la courbe, le sens direct est le sens dans lequel \(t\) augmente. L’application \(t \mapsto f(-t)\) est un autre paramétrage qui définit la seconde orientation.)) et on considère un paramétrage normal \(g:s \mapsto g(s)\) de \(\mathscr{C}\) défini sur un intervalle \(J\).
Si \(M=g(s)\) est un point simple de \(\mathscr{C}\), i.e. l’image d’un seul \(s\) de \(J\), le vecteur \(\overrightarrow \tau (s) = g'(s)\) ne dépend que de \(M\) et non du paramétrage normal \(g\) choisi ; on l’appelle le vecteur unitaire tangent à \(\mathscr{C}\) en \(M\).
Si on change l’orientation de \(\mathscr{C}\), \(\overrightarrow \tau (s)\) est changé en \(-\overrightarrow \tau (s)\).
La droite contenant \(M\) et dirigée par \(\overrightarrow \tau (s)\) est la tangente à \(\mathscr{C}\) en \(M\) ; et la droite contenant \(M\) et orthogonale à \(\overrightarrow \tau (s)\) est la normale à \(\mathscr{C}\) en \(M\).
Lorsque \(s\) varie, la rapidité avec laquelle la direction du vecteur unitaire tangent \(\overrightarrow \tau (s)\) varie est d’autant plus importante que \(\left\| {g^{\prime \prime}(s)} \right\|\) est plus grand. Pour cette raison le nombre \(\left\| {g^{\prime \prime}(s)} \right\|\) s’appelle la {courbure} de \(\mathscr{C}\) en \(M=g(s)\).
On pose \(\gamma (s) = \left\| {g^{\prime \prime}(s)} \right\|\).
Notons que la courbure de \(\mathscr{C}\) en \(M\) est non nulle si et seulement si \(M\) est régulier à l’ordre \(2\). Le nombre \(\rho (s) = \frac{1}{{\left\| {g^{\prime \prime}(s)} \right\|}}\)
s’appelle alors le rayon de courbure de \(\mathscr{C}\) en \(M\).
Si \(\mathscr{C}\) n’admet pas de point d’inflexion, i.e. lorsque \(\left\| {g^{\prime \prime}(s)} \right\| \ne 0\), la fonction
\[\overrightarrow \nu :s \mapsto \frac{{g^{\prime \prime}(s)}}{{\left\| {g^{\prime \prime}(s)} \right\|}}\] est définie sur \(J\) et vérifie \(\left\| {\overrightarrow \nu (s)} \right\| = 1.\)
D’autre part, de la relation
\[{\left\| {g'(s)} \right\|^2}=\left\langle {g'(s),g'(s)} \right\rangle =1,\]
il résulte, par dérivation par rapport à \(s\), que
\[\left\langle {g^{\prime \prime}(s),g'(s)} \right\rangle + \left\langle {g'(s),g^{\prime \prime}(s)} \right\rangle = 2\left\langle {g^{\prime \prime}(s),g'(s)} \right\rangle =0;\]
on a donc
\[\left\langle {\overrightarrow \nu (s),\overrightarrow \tau (s)} \right\rangle=0\]
pour tout élément \(s\) de \(J\).
Le vecteur \(\overrightarrow \nu (s)\) est un vecteur unitaire orthogonal à \(\overrightarrow \tau (s)\).
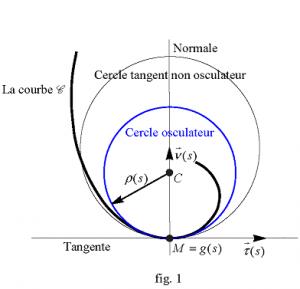
Le point \(C = M + \rho (s)\overrightarrow \nu (s)\) s’appelle le centre de courbure de la courbe \(\mathscr{C}\) en \(M\). Le cercle de centre \(C\) et de rayon \(\rho (s)\) est le cercle de courbure ou le cercle osculateur de \(\mathscr{C}\) en \(M.\) On peut définir le cercle osculateur en \(M\) comme la limite d’un cercle contenant trois points distincts de la courbe, lorsque ces points tendent vers \(M\), en restant sur la courbe. Cette définition est analogue à celle de la tangente en \(M\) comme la limite d’une droite contenant deux points distincts de la courbe, lorsque ces deux points tendent vers \(M\), en restant sur la courbe. Le cercle osculateur en \(M\) approche mieux la courbe au voisinage de \(M\) qu’un cercle tangent quelconque en ce point à la courbe (fig. 1) 1Le cercle osculateur à une courbe en un point constitue une très bonne approximation de la courbe au voisinage de ce point, meilleure qu’un cercle tangent quelconque ; il donne non seulement une idée de la direction dans laquelle la courbe avance (direction de la tangente), mais aussi de sa tendance à tourner de part ou d’autre de la tangente..
.
La déviation d’une courbe plane en un point
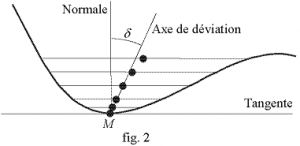
La déviation 2notion introduite par Abel Transon et appelée, par lui, déviation de la forme circulaire ou première déviation de la courbure) ou plus spécifiquement l’aberrance (Le terme déviation a été traduit en anglais par le terme aberrancy, i.e. aberrance, dans le très peu d’endroits où le travail de Transon a été cité. d’une courbe \(\mathscr{C}\) en un point \(M\) est, par définition, la tangente de l’angle \(\delta\) formé par la normale en \(M\) à \(\mathscr{C}\) et la droite, appelée l’axe de déviation ou d’aberrance ou encore la normale affine, limite de la droite déterminée par le point \(M\) et le milieu d’une corde parallèle à la tangente en \(M\) lorsque la corde tend vers cette tangente.
L’angle \(\delta\) est appelé l’angle de déviation (fig. 2).
La déviation mesure l’asymétrie d’une courbe relativement à la normale à la courbe en un point.
.
On essaie de décrire ci-dessous la justification de l’introduction de la notion de déviation, pour une courbe plane ([Référence 10.->#ref10], p. 192-193).
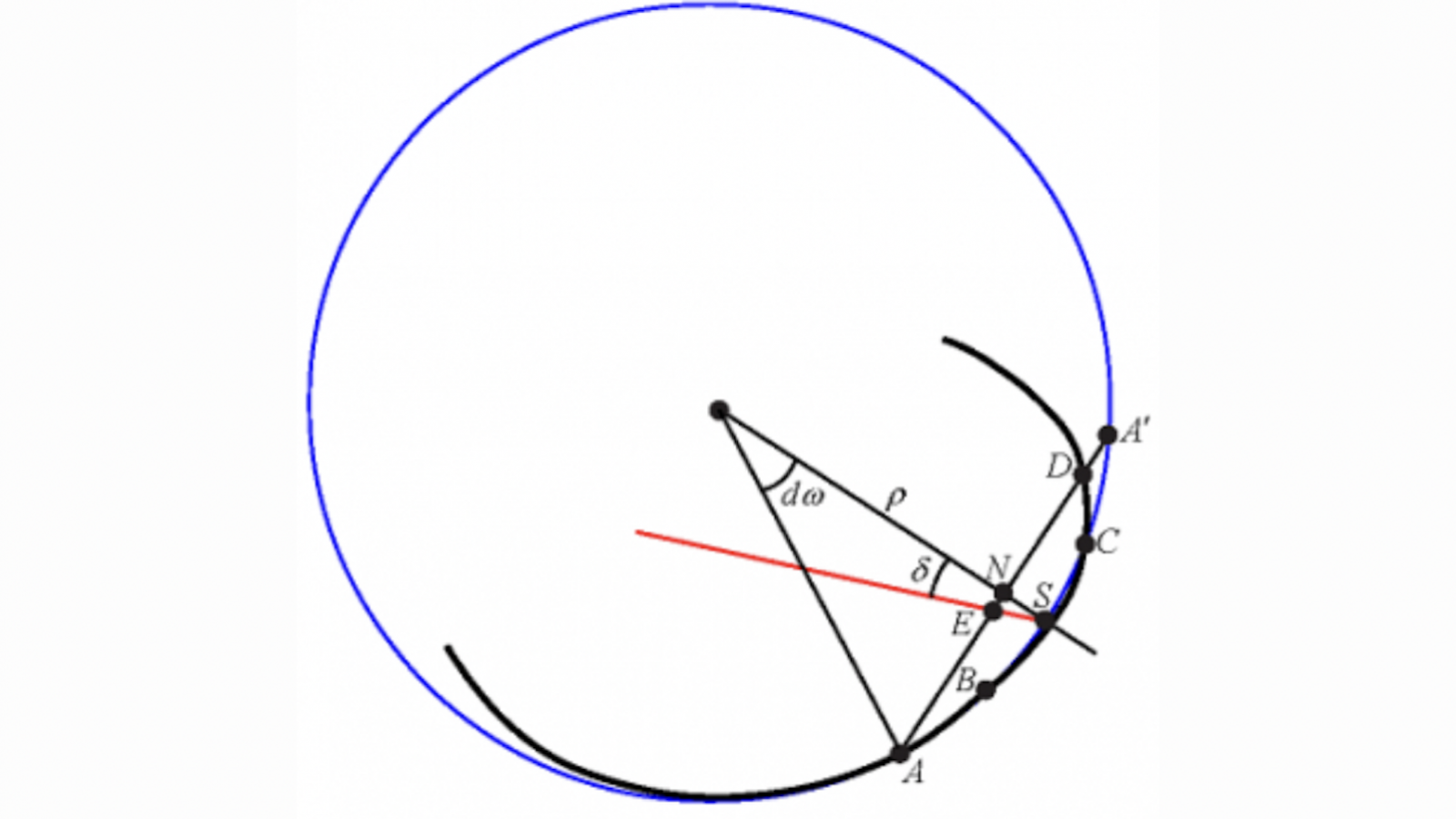
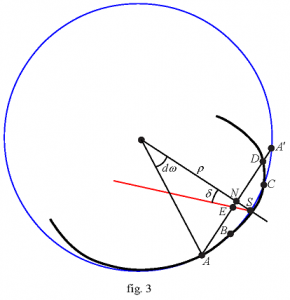
Soient (fig. 3) \(A\), \(B\), \(C\), les trois points consécutifs qui déterminent le cercle osculateur d’une courbe plane ; par le point \(A\) on trace une droite parallèle à l’élément \(BC\). Cette droite rencontre en \(N\) la normale contenant le milieu de \((B, C)\), et le cercle osculateur en \(A’\), tel que \(AN =NA’\) ; enfin elle rencontre la courbe en \(D\) de sorte que la corde \(CD\) soit l’élément consécutif aux éléments \(AB\) et \(BC\).
La distance \(A’D\) (que \(D\) soit à l’intérieur ou à l’extérieur du {disque osculateur}) mesure l’écartement dans l’élément \(CD\) entre la courbe et son cercle osculateur.
Si on désigne par \(f\) la flèche (la longueur du segment d’extrémités le milieu \(S\) de l’arc \(\overset{\displaystyle\frown}{BC}\) et \(N\)), et par \(\delta\) l’angle que fait avec la normale la droite contenant \(S\) et le milieu \(E\) de \((A, D)\), on voit que l’écartement \(A’D\) est égal à \(2f \tan \delta\) (En effet, on a \(\tan\delta = \frac{EN}{f} = \frac{A’D}{2f}\).).
En utilisant la puissance de \(N\) par rapport au cercle osculateur on a
\(f(2\rho –f)=AN^2 = AS^2-f^2\) d’où il vient \(2f = \frac{AS^2}{ \rho}\) ou encore \(2f = \frac{ds^2}{ \rho}\) en identifiant \(AS\) avec la longueur \(ds\) de l’arc \(\overset{\displaystyle\frown}{AS}\) (Il est clair qu’on suppose ici les points \(A\), \(B\), \(C\) et donc \(S\) infiniment proches, ce qui justifiera bien l’identification des “infiniment petits” \(AS\) et \(ds\).). D’où
\[A’D = \frac{{d{s^2}}}{\rho }\tan \delta.\]
Si \(d\omega\) est l’élément d’angle au centre interceptant \(ds\), on a \(ds^2= \rho ^2 d\omega ^2\), puis \[A’D= \rho \tan \delta. d\omega ^2.\]
Pour comparer la grandeur de l’écartement \(A’D\) aux différents points d’une même courbe, on l’évaluera par rapport à des arcs semblables considérés sur les cercles osculateurs particuliers à ces points ; en d’autres termes on regardera \(d\omega\) comme constant.
L’altération de la forme circulaire doit donc se mesurer par \(\frac{{AD’}}{\rho }\), i.e. par \(\tan \delta .d{\omega ^2}\) ou mieux encore par \(\tan \delta \) puisque \(d\omega ^2\) est constant.
C’est cette quantité \(\tan \delta\) que Transon prend pour la seconde affection de la courbure, et qu’il appelle indifféremment déviation de la forme circulaire, ou bien première déviation de la courbure. Il appelle la droite qui fait l’angle \(\delta\) avec la normale {axe de déviation} parce qu’elle apparaît compléter la représentation géométrique ou l’image du polygone infinitésimal par rapport à son troisième élément, comme la tangente et le cercle osculateur sont les images de ce même polygone pour ses deux premiers côtés.
.
Le centre de la conique osculatrice à \(\mathscr{C}\) en \(M\), i.e. l’unique conique qui a un contact d’ordre quatre avec \(\mathscr{C}\) en \(M\), est appelé le {centre de déviation} de \(\mathscr{C}\) en \(M\) ; et la distance du centre de déviation au point de contact \(M\) est appelé le {rayon de déviation}. S’il s’agit de la parabole osculatrice le centre de déviation est, bien entendu, à l’infini, et le rayon de déviation est infini.
Le rayon de déviation dépend de la dérivée d’ordre quatre, et des dérivées d’ordres inférieurs, de la courbe \(\mathscr{C}\) en \(M\). Aussi, le rayon de déviation est une interprétation géométrique de la dérivée d’ordre quatre.
En fait le concept de déviation d’une courbe en un point remonte à trente-huit ans avant la publication de Transon, puisqu’il apparait en 1803 dans Géométrie de position de Lazare Nicolas Marguerite Carnot. Transon n’en a fait aucune mention, comme d’ailleurs ne l’ont pas fait les mathématiciens et les historiens.
Carnot écrit dans Géométrie de position (p. 475-476) :
«Dans toute courbe, il existe pour chaque point une certaine ligne qui ne dépend d’aucune hypothèse particulière, d’aucun terme de comparaison pris dans l’espace absolu ; c’est le rayon de courbure, qui est uniquement déterminé par la forme de la courbe.»
…
«Je crois cependant qu’il est possible de trouver diverses variables qui auroient la condition demandée. Je proposerois par exemple, l’angle que forme au point décrivant la tangente avec la droite qui partage en deux parties égales les sécantes infiniment petites menées dans la courbe, parallèlement à cette tangente.»
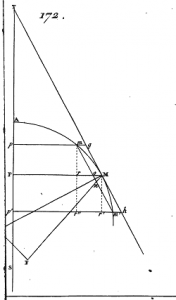
« Imaginons par le point décrivant \(M\) (fig. 172) une tangente \(\overline {MT} \), et une sécante \(\overline {mm’} \), qui lui soit parallèle. Du point \(M\) et par le point milieu \(n\) de cette sécante, imaginons la droite indéfinie \(\overline {MF} \) : concevons maintenant que \(\overline {mm’} \), se rapproche continuellement de \(\overline {MT} \), et finisse par se confondre avec elle. Cela posé, c’est la dernière valeur ou la limite de l’angle \(\widehat {TMF}\) que je proposerois de prendre pour seconde coordonnée ; en prenant pour première le rayon de courbure.
…
On pourroit également prendre l’angle \(\widehat {KMF}\) compris entre cette droite \(\overline {MF} \) et le rayon de courbure.»
.
Comme exemple de l’utilisation de l’angle de déviation comme coordonnée, il donne la parabole définie par l’équation \(y^2=px\) pour laquelle on trouve \[\rho = \frac{1}{2}{\csc ^3}\delta .\]
Cette équation dans laquelle les coordonnées utilisées sont la courbure et la déviation est une forme d’équation intrinsèque pour la parabole.
Carnot donne aussi une relation pour \(\cot \delta\) en soulignant que cette expression est nulle pour un cercle. En d’autres termes cela signifie que la déviation d’un cercle en chacun de ses points est nulle.
Transon qui donna une relation pour \(\tan \delta\) souligna que la déviation est une représentation géométrique de la dérivée d’ordre trois. Il attira aussi l’attention sur quelques propriétés de la déviation des coniques, incluant la relation \(\tan \delta =\frac{1}{3 } \frac{\rho’}{\rho }\) où \(\rho\) est le rayon de courbure de la conique et \(\rho’\) celui de sa développée (La développée d’une courbe est la courbe décrite par le centre de courbure en l’un de ses points \(M\) lorsque \(M\) décrit cette courbe.)
Notons qu’en un point \(M\) où le rayon de courbure \(\rho\) a un extremum, la courbe, dans un voisinage de \(M\) est située à l’intérieur ou à l’extérieur du disque délimité par le cercle osculateur, et si dans un voisinage de \(M\) la courbure de la courbe décroît d’une façon monotone, alors la courbe passe en \(M\) d’un côté du cercle osculateur à l’autre.
La grandeur qui mesure la “déviation” de la courbe de son cercle osculateur est précisément la déviation (de Transon) comme cela a été vu ci-dessus.
Donc, si la courbure d’une courbe en un point donne une mesure de la « non-linéarité » de cette courbe au voisinage de ce point, la déviation donne, quand à elle, une mesure de la « non-circularité » de la dite courbe, i.e. la quantité dont la courbe proposée s’écarte de la forme circulaire.
On peut aussi définir la déviation d’un point de vue de contact de courbes. Intuitivement, le cours de la courbe près du point \(M\) est reproduit avec une précision du troisième ordre par la parabole osculatrice qui a un contact d’ordre trois avec la courbe en \(M\), et qui est obtenue comme la limite d’une parabole contenant \(M\) et trois autres points de la courbe, voisins de \(M\), lorsque ces trois points tendent vers \(M\) (la parabole osculatrice contient quatre points infiniment voisins de la courbe).
On a \[\tan \delta = \frac{1}{3}\frac{{d\rho }}{{ds}}\]
où \(\rho\) est le rayon de courbure et \(s\) la longueur de la courbe en \(M.\)
Pour une courbe définie par le paramétrage \[t \mapsto \left( {x(t),y(t)} \right),\] l’expression de la déviation est donnée par
\[\tan \delta = \frac{{x’x^{\prime \prime}+ y’y ^{\prime \prime}}}{{x’y^{\prime \prime} – x^{\prime \prime}y’}} – \frac{{\left( {{{x’}^2} + {{y’}^2}} \right)\left( {x’y ^{\prime \prime\prime} – x ^{\prime \prime\prime}y’} \right)}}{{3{{(x’y^{\prime \prime} – x^{\prime \prime}y’)}^2}}}.\]
qui montre bien que la déviation est caractérisée par les dérivées d’ordre trois.
La déviation est nulle en tout point d’un cercle comme il a été noté ci-dessus, et une constante non nulle en tout point d’une spirale logarithmique.
L’angle de déviation \(\delta\) est l’angle de la normale à la courbe en \(M\) et l’axe de la parabole osculatrice à la courbe en \(M\).
L’axe de déviation d’une conique en un de ses points est la droite contenant ce point et le centre de la conique.
En un point \(M\) d’une courbe quelconque les coniques ayant un contact du troisième ordre avec la courbe ont même axe de déviation (cf encart “Plus d’explications”). En un point de rencontre de deux coniques homofocales, les axes de déviation des deux coniques coïncident.
Notons, pour l’occasion, que l’axe de déviation en \(M\) est la directrice d’une parabole remarquable appelée la parabole de Transon dont le foyer est le symétrique par rapport à la normale en \(M\) du projeté orthogonal du centre de courbure sur l’axe de déviation.


Plus d'explications...
Soient \(\mathscr{C_1}\) et \(\mathscr{C_2}\) deux courbes de classe \(C^{k}\) (\(k \ge 1\)), simples et régulières se rencontrant en \(M_0\). On dit que \(\mathscr{C_1}\) et \(\mathscr{C_2}\) sont en contact à l’ordre \(p\) (\(0 \le p \le k\)) en \(M_0\) s’il existe des paramétrages \(\phi\) et \(\psi\) de \(\mathscr{C_1}\) et \(\mathscr{C_2}\) respectivement, définis sur un intervalle \(I\), qui soient en contact à l’ordre \(p\) en \(t_0\) où \[{t_0} = {\mathop \phi \limits^{ – 1}}({M_0}) = {\mathop \psi \limits^{ – 1} }({M_0}),\] c’est-à-dire qui soient tels que pour tout \(\varepsilon\), réel strictement positif, il existe un voisinage \(V\) de \(x_0\) tel que pour tout point \(x\) de \(V \cap I\),\[\left\| {{\phi}(x) – {\psi}(x)} \right\| \le \varepsilon {\left| {x – {x_0}} \right|^p}.\] On a alors \(\phi (x_0)= \psi (x_0)\) et
\(\lim_{{x \to x_0 , x \ne x_0}}\frac{{\varphi (x) – \psi (x)}}{{{{(x – {x_0})}^p}}} = 0\).
Références
1. Cameron Byerley and Russel A. Gordon, Measures of Aberrancy, Real Analysis Exchange, Vol. 32(1), 2006/2007, p. 233–266.
2. L. N. M. Carnot, Géométrie de position. De l’Imprimerie de Chapelet. A Paris, Chez J. B. M. Duprat, Librairie pour les Mathématiques, quai des Augustins. AN XI – 1803, p. 475-476.
3. V. V. Chernikov, S. A. Kopanev, Aberrancy of Level Lines and Their Orthogonal Trajectories for Univalent Conformal Mappings, Siberian Mathematical Journal, March-April, 1986, Volume 27, Issue 2, p. 298-305.
4. Hamza Khelif, Le jardin des courbes, Dictionnaire raisonné des courbes planes célèbres et remarquables, 2e édition (Manuscrit).
5. J. W. Lasley, Jr., On the Equations of Certain Osculants, Journal of The Mitchell Society, August 1945, p. 48-54.
6. J. W. Lasley, Jr., Penosculating Conics of a Plane Curve, Bulletin of the American Mathematical Society, 37 (1931), no. 2, 76-82.
7. M. A. Pellet, Construction des rayons de courbure d’une classe de courbes et de surfaces, Bulletin de la S. M. F., tome 35 (1907), p. 76-80.
8. Steven H. Schot, Geometrical Properties of the Penosculating Conics of a Plane Curve, The American Mathematical Monthly, Vol. 86, No. 6 (Jun.-Jul., 1979), p. 449-457.
9. Steven H. Schot, Aberrancy : geometry of the third derivative, Math. Mag., 51 (1978), 259–275.
10. A. Transon, Recherches sur la courbure des lignes et des surfaces, Journal de Mathématiques pures et appliquées par Joseph Liouville, Tome 6, 1841.
11. E. J. Wilczynski, Some Remarks on the Historical Development and the Future Prospects of the Differential Geometry of Plane Curves, Bulletin of the American Mathematical Society, 22 (1916) 317-329.


Il est possible d’utiliser des commandes LaTeX pour rédiger des commentaires — mais nous ne recommandons pas d’en abuser ! Les formules mathématiques doivent être composées avec les balises .
Par exemple, on pourra écrire que sont les deux solutions complexes de l’équation .
Si vous souhaitez ajouter une figure ou déposer un fichier ou pour toute autre question, merci de vous adresser au secrétariat.