L’idée que les courbes n’ont pas d’épaisseur et que par conséquent elles ont une aire nulle, qu’il y a moins de points dans un segment de droite qu’à l’intérieur d’un carré, était un héritage mathématique indiscuté depuis toujours ; mais finalement cette idée a dû être abandonnée. Depuis plus d’un siècle les mathématiciens s’étaient posés la question de l’existence de courbes qui passent par tous les points de parties de mesure (aire, volume…) non nulle du plan ou de l’espace, telles que l’intérieur d’un carré dans le plan par exemple ; en d’autres termes, des courbes qui remplissent ces parties, et donc des courbes dont l’aire n’est pas nulle ! 8En 1878 G. Cantor démontra l’existence d’une bijection entre un intervalle et un carré, ou un cube. En 1879, G. Netto prouva qu’une telle bijection est nécessairement discontinue (The Theory of Functions of a Real Variable and The Theory of Fourier’s Series, by E. W. Hobson, Cambridge University Press, pp. 329, 330). On se débarrassa de la condition de bijectivité et la question de l’existence de courbes de Jordan (applications continues et injectives de l’intervalle dans le plan ou l’espace) de mesure non nulle prit place. Une réponse positive fut donnée en 1903 par W. F. Osgood quand il construisit une famille à un paramètre de telles courbes. Ces courbes ont une mesure de Lebesgue non nulle et l’arc limitant la famille est une courbe de Peano. En 1917 K. Knopp donna une autre famille de courbes dont l’arc limite est la courbe de Sierpinski. (5. pages 1 et 2)
Courbes d’aire nulle
Courbes d’aire ou de volume non nul
G. Peano fut le premier à donner une réponse positive à cette question en construisant en 1890 le premier exemple d’une telle courbe 9“Sur une courbe qui remplit toute une aire plane”, Math. Ann., vol. XXXVI, 1890..
D’autres exemples furent ensuite donnés par D. Hilbert en 1891, E. H. Moore en 1900, H. Lebesgue en 1904, W. Sierpinski en 1912, G. Polya en 1913… Les mathématiciens appellent désormais les courbes définies par des méthodes itératives ayant cette propriété, courbes de Peano, courbes de remplissage ou encore courbes remplissantes. Les figures de 1 à 6 représentent respectivement des courbes approchées de ces six courbes 10Pour des détails sur la définition et les propriétés de ces courbes consulter les références ou voir ici..
De gauche à droite, figures 1 à 3
De gauche à droite figures 4 à 6
Ces constructions se généralisent aisément dans l’espace.
Dimension fractale
On ne s’intéresse plus à la dimension topologique de ces courbes mais plutôt à la dimension fractale (introduite par Benoît Mandelbrot)
\[
d = \mathop {\lim }\limits_{\varepsilon \to 0} \left( {\frac{{\ln {N_\varepsilon }}}{{ – \ln \varepsilon }}} \right)
\]
où \(N_\varepsilon\) est le nombre minimal de boules de rayon \(\varepsilon\) couvrant la courbe.
Cette dimension, comprise entre 0 et 1 (resp. 1 et 2, 2 et 3), correspond à la capacité d’un ensemble de points (resp. d’une ligne, d’une surface) de remplir partiellement une ligne (resp. un plan, un volume) sans y parvenir complètement faute d’avoir la valeur entière 1 (resp.2, 3) de la dimension topologique qui seule le permet. Par exemple la dimension fractale des courbes citées ci-dessus est 2.
Notons que ces courbes sont continues et certaines, comme celle de Lebesgue par exemple, possèdent une tangente en presque tout point. On montre cependant qu’une courbe de Peano admettant une tangente en chacun de ses points n’existe pas.
Ces résultats peuvent se généraliser à d’autres parties du plan ou de l’espace mais leurs énoncés sont plus techniques 11Comme par exemple ce théorème de Hahn-Mazurkiewicz : un espace topologique de Hausdorff (séparé) non vide peut être complètement rempli par une courbe continue si, et seulement si, il est compact, connexe, localement connexe et métrisable. Felix Hausdorff avait déjà demontré que “Tout ensemble compact est une image continue de l’Ensemble de Cantor.” (Set Theory, Chelsea, New York 1962, pp. 154, 226.).
Les courbes de remplissage qui forment déjà une partie de la « géométrie fractale » étudiée notamment par Benoît Mandelbrot, continuent à intéresser les mathématiciens et les informaticiens non seulement à cause de leur caractère récréatif et leur structure récursive élégante, mais aussi parce qu’elles se sont avérées utiles dans beaucoup de domaines scientifiques. Un exemple simple est la résolution du problème dit du « voyageur de commerce » : « Étant donnés n points (des villes) et les distances séparant chaque paire de points, trouver un chemin de longueur totale minimale qui passe exactement une fois par chaque point et revienne au point de départ » (Voir fig.7 où une « bonne » solution est donnée par la courbe de Hilbert) 12Pour des applications en combinatoire voir par exemple ici et pour un peu d’art géométrique abstrait voir ici. Ces courbes ont pris leur place dans les systèmes de compression d’images, en imagerie pour faire des parcours aléatoires de surfaces, ce qui donne des fonds esthétiques à certaines images (dithering qui signifie juxtaposition de points, mélange de points de couleurs différentes pour élaborer des couleurs intermédiaires), en imagerie médicale, etc..
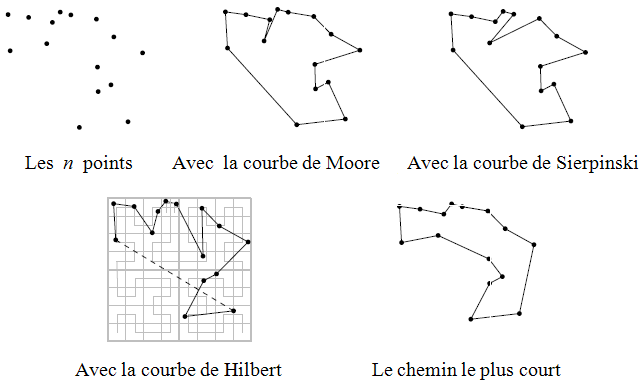
Figure 7
Une généralisation : les courbes \(\alpha\)-denses
Si les courbes qui remplissent une partie d’un espace passent par tous les points de cette partie, il existe d’autres types de courbes n’ayant pas ce privilège mais qui peuvent néanmoins s’approcher de chaque point de cette partie d’une distance inférieure ou égale à un nombre positif fixé \(\alpha\). On les appellera les courbes \(\alpha\)-denses 13Ces courbes sont largement utilisées en optimisation globale (le problème du “sac à dos” et le problème de “transport” par exemple, y sont étudiés), en biomédecine, etc..
Par exemple, la spirale d’Archimède définie en coordonnées polaires par l’équation
\[\rho = a\theta\]
est \(\pi a\)-dense dans le plan. (fig. 8)
En effet, tout point du plan appartient à un segment (ouvert à droite) dont les extrémités appartiennent à la spirale, c’est-à-dire de la forme [\((a\theta, \theta),
(a(\theta+2\pi), \theta)\)[ et sa distance à l’une des extrémités est inférieure à la moitié de la longueur de ce segment, à savoir \(\pi a\).
Plus généralement
Plus généralement
Soit \(\alpha\in\bf R^+\). Un sous-espace \(A\) d’un espace métrique \((E, d)\), est dit \(\alpha\)-dense dans} \(E\) si
\[\forall m\in E, \exists m’\in A : d(m,m’)\leq \alpha.\]
Une courbe \(\gamma\) est \(\alpha\)-dense dans un sous-espace \(K\) de} \({\bf R^n}\) si \(\gamma\) en tant que sous-espace de \(K\) est \(\alpha\)-dense dans \(K\), i.e. si
\[\forall m\in K, \exists m’\in \gamma : d(m,m’)\leq \alpha.\]
Il est immédiat que si une courbe est \(\alpha\)-dense dans \(K\), alors elle est \(\beta\)-dense dans \(K\) pour tout \(\beta\) tel que \(\alpha\leq \beta\).
Figure 8
On peut donc considérer une courbe qui remplit un espace comme une courbe \(0\)-dense dans cet espace puisque dans ce cas tout point de l’espace en question coïncide avec un point de la courbe.
Pour plus de détails sur les courbes \(\alpha\)-denses et leurs domaines d’applications se reporter par exemple à la référence 1.
Si on se permet de s’enfoncer un peu plus dans cette « forêt dense » des courbes, on peut remarquer l’existence de courbes \(\alpha\)-denses pour tout \(\alpha\) strictement positif. Ce sont les courbes dites denses (puisque c’est indépendant de \(\alpha\), on s’en débarrasse!) et qui seront appelées dans ce texte courbes de remplissage faible.
Une courbe remplit faiblement une partie du plan ou de l’espace est donc une courbe qui est presque partout présente dans cette partie, puisqu’elle peut approcher chacun de ses points d’aussi près que l’on veut 14Dans la vie de tous les jours le remplissage est tout à fait relatif. Par exemple une boite « remplie » de cailloux d’une taille donnée peut contenir davantage de cailloux de plus petite taille, de sable, d’eau, etc.. Dans ce qui suit on en donne quelques exemples définis par des représentations paramétriques simples.
Les courbes définies en coordonnées cartésiennes par les équations paramétriques
\[x = a\cos \alpha t,\;y = b\sin \beta t\]
avec \(a\) et \(b\) positifs et \(\frac{\alpha}{\beta}\) irrationnel, remplissent faiblement le rectangle \([-a,a]\times[-b,b]\).
Par exemple la courbe définie par les équations
\[x = \cos \sqrt 2 t,\,\,y = \sin t\]
remplit faiblement le carré \([-1,1]^2\) (la courbe ne contient pas par exemple le centre du carré). (fig. 9)
La figure 10 représente le cube \([-1,1]^3\) faiblement rempli par la courbe définie par la paramétrisation
\[x = \cos \sqrt 3 t,\,\,y = \cos \sqrt 2 t,\,z = \sin\pi t.\]
De même les courbes définies en coordonnées polaires par l’équation
\[\rho= a + b\cos \alpha \theta \]
avec \(a\) et \(b\) positifs et \(\alpha\) irrationnel, remplissent faiblement la couronne \(\left| {a – b} \right| \le \rho \le a + b\). Par exemple la courbe définie par
\[\rho=2+\cos\sqrt{2}\theta \]
remplit faiblement la couronne définie par \(1\le\rho\le3\). (fig. 11)
De gauche à droite, figures 9 à 11
Références
1. Optimisation globale Théorie des courbes α-denses par Yves CHERRUAULT et Gaspar MORA, Economica, 2005.
2. Chaos and Fractals New Frontiers of Science, by Heinz-Otto PEITGEN, Hartmut JÜRGENS, Dietmar SAUPE, Springer, 2004.
3. Le jardin des courbes Dictionnaire raisonné des courbes planes célèbres et remarquables, par Hamza KHELIF. Ellipses, 2010.
4. http://www.mathcurve.com/ de Robert FERRÉOL.
5. Space-Filling Curves by Hans SAGAN. Springer-Verlag, 1994.
Voir aussi cette Page.
ÉCRIT PAR
Hamza Khelif
Enseignant de mathématique - El-Oued - Algérie
