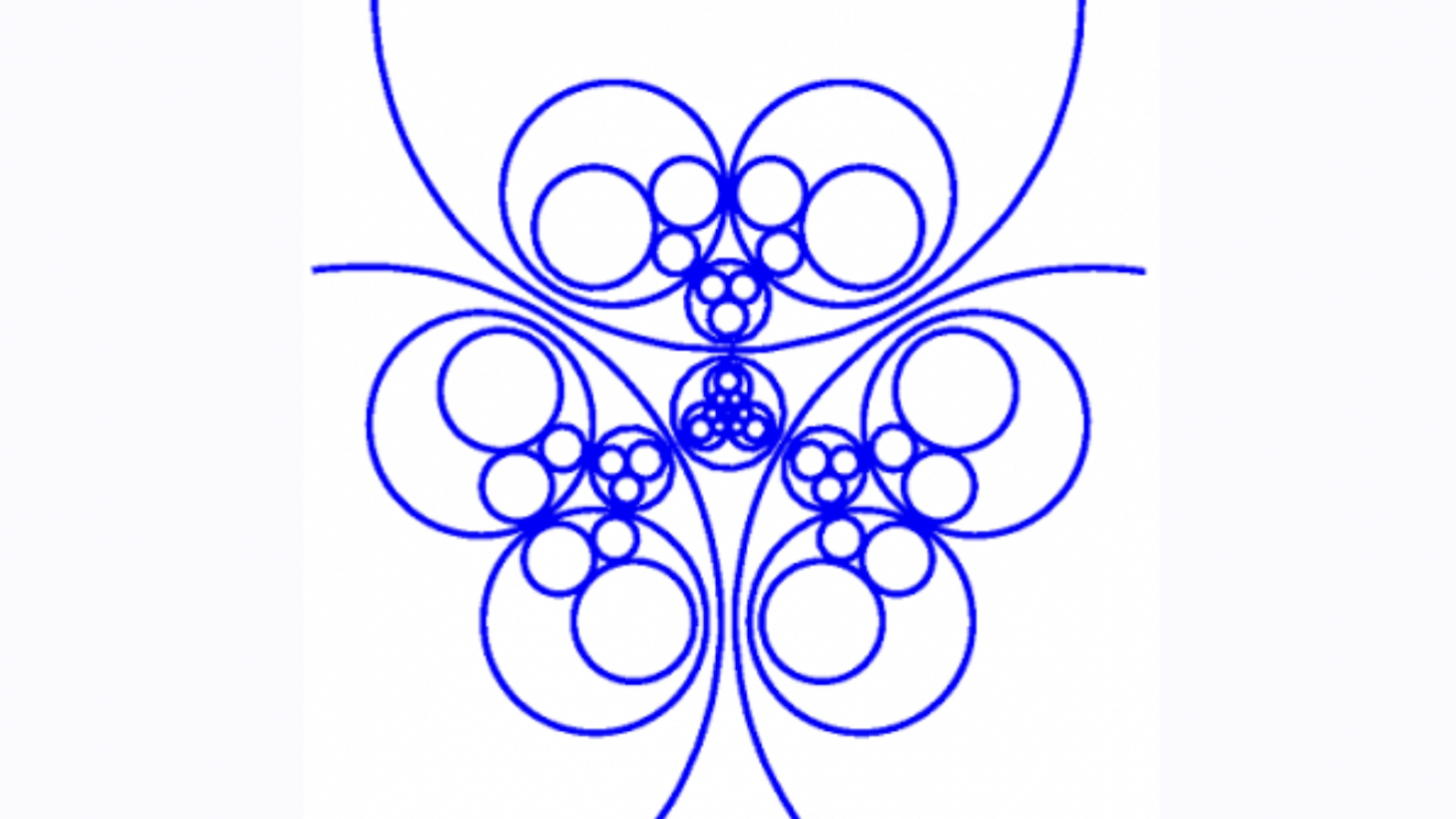
L’inversion circulaire, bien que ne figurant plus dans les programmes d’enseignement depuis quelques décennies, est relativement ancienne. C’est une source de beaucoup de beautés mathématiques. On trouve ses diverses applications en géométrie, en mécanique et en cartographie. Elle permet, par exemple, la transformation d’un mouvement circulaire en un mouvement rectiligne 11L’inversion par rapport à une sphère (dans l’espace où nous vivons) permet de peindre la face interne d’un ballon sans le couper et permet aussi d’enfermer un lion dans une cage en faisant seulement bien attention de ne pas s’y enfermer avec lui.. L’inversion par rapport à une conique quelconque, quant à elle, est tout à fait nouvelle, mais l’inversion par rapport à une courbe algébrique quelconque n’est pas (à ma connaissance) encore définie. 12Les dessins ainsi que le contenu de ce texte sont tirés de la référence 4. dans lequel on trouve également une généralisation de l’inversion à une courbe algébrique plane de degré n, n⩾3, quelconque comme courbe directrice mais qui se base sur des notions géométriques qui demandent à elles seules un article à part..
L’inversion circulaire
Étant donnés un point \(\omega(x_0 ,y_0)\) du plan \({\cal E}_2\) et un réel \(k\) non nul, l’inversion de pôle \(\omega\) et de puissance \(k\) est la transformation (conforme 13Une transformation conforme \(f\) dans le plan est une transformation d’un domaine du plan dans un plan, qui conserve (localement) les angles entre deux courbes orientées, c’est-à-dire que si deux courbes \({\cal C}_1\) et \({\cal C}_2\) se rencontrent en \(A\), et que leurs vecteurs tangents en \(A\) (dans le sens de l’orientation) forment un angle de mesure \(\alpha\), les vecteurs tangents en \(f(A)\) aux deux courbes images \(f({\cal C}_1)\) et \(f({\cal C}_2)\) forment également un angle de mesure \(\alpha\). Autrement dit, \(f\) est localement une similitude directe. Voir cet article. Voir également ici ou encore là.)\(\mathscr{I}_{(\omega,k)}\) de \({\cal E}_2 \setminus \lbrace \omega \rbrace\) dans lui-même qui associe au point \(M\) le point \(M’\) tel que \(M’ \in (\omega M)\) et \(\overline {\omega M} .\overline {\omega M’} = k\). Cette involution est définie en coordonnées cartésiennes par les relations
\[x’ = x_0 + \frac{{k(x – {x_0})}}{{{{(x – {x_0})}^2} + {{(y – {y_0})}^2}}}\]
Le cercle \(\mathscr{C}(\omega,\sqrt k)\), imaginaire si \(k<0\), est invariant point par point ; c’est le cercle d’inversion. On dit que \(\mathscr{I}\) est l’inversion par rapport à ce cercle. Les droites contenant le pôle \(\omega\) et les cercles tels que la puissance de \(\omega\) par rapport à eux égale \(k\) (ils forment un réseau 14Un réseau non dégénéré de cercles est l’ensemble de tous les cercles par rapport auxquels un point donné, le centre du réseau, a une puissance donnée. Un réseau dégénéré de cercles est l’ensemble de tous les cercles dont les centres appartiennent à une droite donnée, dite droite fondamentale.), orthogonaux au cercle d’inversion, sont globalement invariants. L’inverse d’un cercle ne contenant pas le pôle est un cercle. Celle d’un cercle contenant ce pôle est une droite 15De là résulte la transformation d’un mouvement circulaire en un autre rectiligne.. Voir les notes [7] et [8] de cet article.
On prolonge l’inversion \(\mathscr{I}\) à \({\cal E}_2 \cup \lbrace \infty \rbrace \) par \(\mathscr{I}(\omega) = \infty \) et \(\mathscr{I}(\infty ) = \omega \).
L’inverse d’une courbe algébrique de degré \(n\) admettant les points cycliques comme points d’ordre \(p\) par rapport à un point d’ordre \(q\) est une courbe
algébrique de degré \(2n-2p-q\) admettant les points cycliques comme points d’ordre \(n-p-q\) et le pôle comme point d’ordre \(n-2p.\)
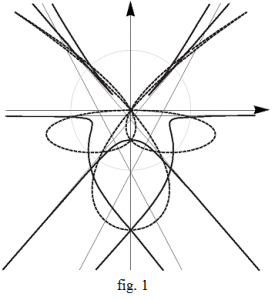
La figure 1 représente l’inverse (en trait continu), par rapport au cercle unité, de la courbe définie par la paramétrisation
\[x = \cos t + \sin 4t,y = \cos 2t + \sin 3t.\]
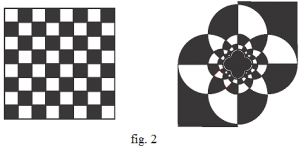
La figure 2 montre un échiquier de centre \((0,0)\) et son image par une inversion de pôle \((0,0)\) et de petite puissance 16M. Gardner, The Sixth Book of Mathematical Diversions, University of Chicago Press,1984, p. 244-245..
L’inversion par rapport à une conique
On donne d’abord la définition générale de l’inversion par rapport à une conique quelconque. On la définira ensuite séparément pour chacune des trois coniques propres.
Rappelons que l’ensemble des conjugués 17On dit que les points \(M_0\) et \(M’\) sont conjugués par rapport à une conique \(\cal C\) si la droite \((M_0M’)\) rencontre la conique \(\cal C\) en deux points \(P\) et \(Q\) tels que la division \([M_0, M’, P, Q]\) soit harmonique, i.e. tels que \[\frac{{\overline {P{M_0}} }}{{\overline {PM’} }} = – \frac{{\overline {Q{M_0}} }}{{\overline {QM’} }}.\] d’un point \(M_0\) par rapport à une conique propre est une droite appelée {la polaire} de \(M_0\) par rapport à cette conique.
Cette droite contient les points de contact des tangentes (réelles ou non), contenant \(M_0\).
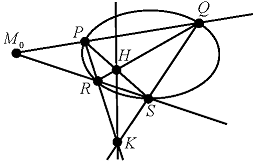
Soient deux droites quelconques contenant \(M_0\) et rencontrant la conique en \(P\), \(Q\) et \(R\), \(S\), alors la polaire de \(M_0\) contient les points \(K\), commun aux droites \((PR)\) et \((QS)\), et \(H\), commun à \((PS)\) et \((QR)\) .
La polaire d’un point de la conique est la tangente en ce point.
On peut alors définir l’inversion de pôle \(\omega\) par rapport à une conique \(\cal C\), dans le plans \({\cal E}_2\), comme étant la transformation de \({\cal E}_2 \setminus \lbrace \omega \rbrace\) dans lui-même qui au point \(M\) associe le point \(M’\) rencontre de la droite \((\omega M)\) avec la polaire de \(M\) par rapport à \(\cal C.\)
Soit \(\cal C\) la conique la plus générale, définie par l’équation
\[a{x^2} + 2bxy + c{y^2} + 2dx + 2ey + f = 0.\]
L’équation de la (droite) polaire du point \(M(\lambda ,\mu )\) par rapport à \(\cal C\) est donnée par l’équation
\[\left( {d + a\lambda + b\mu } \right)x + \left( {e + b\lambda + c\mu } \right)y + f + d\lambda + e\mu = 0.\]
L’inversion de pôle \(\omega (x_0 ,y_0 )\) par rapport à cette courbe est alors définie par les relations
\[\eqalign{
& x’ = – \frac{{\left( {f + dx + ey} \right)\left( {x – x_0 } \right) + \left( {e + bx + cy} \right)\left( { – yx_0 + xy_0 } \right)}}{{\left( {d + ax + by} \right)\left( {x – x_0 } \right) + \left( {e + bx + cy} \right)\left( {y – y_0 } \right)}}, \cr
& y’ = – \frac{{\left( {f + dx + ey} \right)\left( {y – y_0 } \right) – \left( {d + ax + by} \right)\left( { – yx_0 + xy_0 } \right)}}{{\left( {d + ax + by} \right)\left( {x – x_0 } \right) + \left( {e + bx + cy} \right)\left( {y – y_0 } \right)}}. \cr} \]
L’inversion elliptique
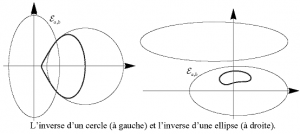
Soit \({\cal E}_{a,b}\) l’ellipse du plan \({\cal E}_2\) de centre \(O\) et de demi-axes \(a\) et \(b\). L’inversion de pôle \(O\) par rapport à \({\cal E}_{a,b}\) est la transformation de \({\cal E}_2 \setminus \lbrace O \rbrace\) dans lui-même qui au point \(M\) associe le point \(M’\) de la demi-droite \([OM)\) tel que \[\overline {OM} .\overline {OM’} = {OI^2}\] où \(I\) est le point de rencontre de \([OM)\) avec l’ellipse \({\cal E}_{a,b}\). Le point \(O\) est appelé le centre ou le pôle de l’inversion et \(OI\) son rayon. \({\cal E}_{a,b}\) est l’ellipse de l’inversion. C’est l’ensemble des points invariants par cette inversion. L’inverse \(M’\) de \(M\) est la rencontre de la droite \((OM)\) avec la polaire de \(M\) par rapport à \({\cal E}_{a,b}\) 18On peut donc, en considérant la définition d’une inversion de directrice une conique quelconque donnée ci-dessus, définir l’inversion par rapport à une ellipse, de pôle un point arbitraire du plan qui le contient. et on a
\[\overline {OM} .\overline {OM’} = \frac{{{a^2}{b^2}\left( {1 + {m^2}} \right)}}{{{b^2} + {a^2}{m^2}}}\]
où \(m\) est la pente de la droite \((OM)\) mesurée à partir de l’axe principal de la conique. Si \(m\) est infinie alors \[\overline {OM} .\overline {OM’} = {b^2}.\]
Si l’ellipse \({\cal E}_{a,b}\) est définie par l’équation \[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} – 1 = 0\] alors l’inversion par rapport à \({\cal E}_{a,b}\) est définie par \[(x,y) \mapsto \left( {\frac{{{a^2}{b^2}x}}{{{b^2}{x^2} + {a^2}{y^2}}},\frac{{{a^2}{b^2}y}}{{{b^2}{x^2} + {a^2}{y^2}}}} \right).\]
L’inversion par rapport à une ellipse est involutive.
Une droite contenant le pôle de l’inversion est globalement invariante.
L’image d’une droite ne contenant pas le pôle est une ellipse qui contient ce pôle.
L’inverse d’une conique qui n’est pas de la même semi-forme que l’ellipse d’inversion (être de la même semi-forme signifie ici que les coniques sont de même excentricité et que leurs axes sont respectivement parallèles) et contenant le pôle est une cubique.
L’inverse d’une conique qui n’est pas de la même semi-forme que l’ellipse d’inversion et ne contenant pas le pôle est une quartique.
L’inverse d’une courbe définie par le paramétrage
\[t \mapsto \left( {f(t),g(t)} \right)\]
est définie par le paramétrage \[t \mapsto \left( {\frac{{{a^2}{b^2}f(t)}}{{{b^2}f{{(t)}^2} + {a^2}g{{(t)}^2}}},\frac{{{a^2}{b^2}g(t)}}{{{b^2}f{{(t)}^2} + {a^2}g{{(t)}^2}}}} \right).\]
Il n’est pas inutile de remarquer que l’inversion circulaire est un cas particulier très important de l’inversion elliptique, le cercle est une ellipse particulière.
L’inversion hyperbolique
Soit \({\cal H}_{a,b}\) l’hyperbole du plan \({\cal E}_2\) de centre \(O\) et de demi-axes \(a\) et \(b\). L’inversion par rapport à \({\cal H}_{a,b}\) est la transformation de \({\cal E}_2 \setminus \lbrace O \rbrace\) dans lui-même qui au point \(M\) associe le point \(M’\) de la droite \((OM)\) tel que
\[\overline {OM} .\overline {OM’} = \frac{{{a^2}{b^2}\left( {1 + {m^2}} \right)}}{{{b^2} – {a^2}{m^2}}}\]
où \(m\) est la pente de la droite \((OM)\) mesurée à partir de l’axe principal de la conique.
Si \(m\) est infinie alors \[\overline {OM} .\overline {OM’} = -{b^2}.\] Le point \(O\) est appelé le centre ou le pôle de l’inversion et \({\cal H}_{a,b}\) est l’hyperbole de l’inversion 19On peut aussi pour le cas hyperbolique, définir l’inversion de directrice une hyperbole donnée et de pôle un point quelconque de son plan..
Si l’hyperbole \({\cal H}_{a,b}\) est définie par l’équation \[\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} – 1 = 0,\]
alors l’inversion par rapport à \({\cal H}_{a,b}\) est définie par
\[(x,y) \mapsto \left( {\frac{{{a^2}{b^2}x}}{{{b^2}{x^2} – {a^2}{y^2}}},\frac{{{a^2}{b^2}y}}{{{b^2}{x^2} – {a^2}{y^2}}}} \right).\]
L’inversion par rapport à une hyperbole est involutive.
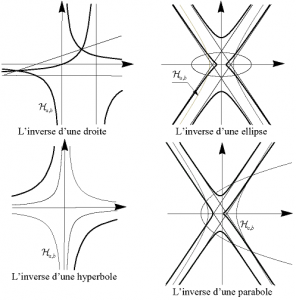
L’inverse d’une droite parallèle à une asymptote est une droite parallèle à l’autre asymptote.
L’inverse d’une droite non parallèle à une asymptote est une hyperbole contenant le pôle et ses asymptotes sont parallèles à celles de l’hyperbole de l’inversion.
L’inverse d’une hyperbole ne contenant pas le pôle et dont les asymptotes sont parallèles à celles de l’hyperbole de l’inversion est une hyperbole jouissant des mêmes propriétés ; si l’hyperbole à inverser est centrée au pôle, son image est aussi centrée au pôle.
L’inverse d’une courbe définie par le paramétrage
\[t \mapsto \left( {f(t),g(t)} \right)\]
est définie par le paramétrage
\[t \mapsto \left( {\frac{{{a^2}{b^2}f(t)}}{{{b^2}f{{(t)}^2} – {a^2}g{{(t)}^2}}},\frac{{{a^2}{b^2}g(t)}}{{{b^2}f{{(t)}^2} – {a^2}g{{(t)}^2}}}} \right).\]
L’inversion parabolique
Soit \({\cal P}\) la parabole définie en coordonnées cartésiennes par l’équation
\[y^2-2px=0\]
et soit \(\omega ({x_0},{y_0})\) un point donné du plan.
La polaire d’un point quelconque \(M(\alpha ,\beta )\) par rapport à \({\cal P}\) est définie par l’équation cartésienne \[px – \beta y + p\alpha = 0.\]
Pour tout point \(M\) distinct de \(\omega\) la rencontre de la droite \((\omega M)\) avec la polaire de \(M\) relativement à \({\cal P}\) est le point \(M’\) de coordonnées
\[\alpha ‘ = – \frac{{p{\alpha ^2} – p\alpha {x_0} + {\beta ^2}{x_0} – \alpha \beta {y_0}}}{{p\alpha – {\beta ^2} – p{x_0} + \beta {y_0}}},\]
\[\beta ‘ = – \frac{{p\left( {\alpha \beta + \beta {x_0} – 2\alpha {y_0}} \right)}}{{p\alpha – {\beta ^2} – p{x_0} + \beta {y_0}}}.\]
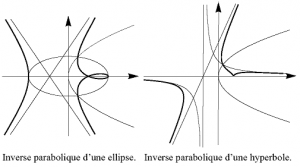
L’inversion \(\mathscr{I}_{(\omega ,\cal P)}\) de pôle \(\omega\) par rapport à la parabole \({\cal P}\), ou inversion parabolique de pôle \(\omega\), est la transformation du plan qui au point \(M(x,y)\) distinct de \(\omega\) associe le point \(M'(x’,y’)\) défini comme ci-dessus.
L’inverse parabolique, de pôle \(\omega\), de la courbe définie par la paramétrisation
\[x=f(t),y=g(t)\]
est donnée par la paramétrisation
\[x = – \frac{{p f{{(t)}^2} – p f(t){x_0} + g{{(t)}^2}{x_0} – f(t)g(t){y_0}}}{{pf(t) – g{{(t)}^2} – p{x_0} + g(t){y_0}}},\]
\[y = – \frac{{p\left({f(t)g(t) + g(t){x_0} – 2f(t){y_0}} \right)}}{{pf(t) – g{{(t)}^2} – p{x_0} + g(t){y_0}}}.\]
La (droite) polaire d’un point d’une conique relativement à cette conique étant la tangente en ce point, la courbe directrice de l’inversion est invariante point par point par cette inversion ; il s’ensuit que la courbe image contient les points de rencontre éventuels de la courbe de départ avec la directrice 20Cet énoncé est bien entendu valable pour toutes les inversions considérées dans cet article.
Références
1. David E. Blair, Inversion Theory and Conformal Mapping, American Mathematical Society, 2000.
2. R. Caddeo, G. Franzoni, P. Piu, Inverting Beauty, Dipartimento diMatematica e Informatica, Universit`a degli Studi di Cagliari, Via Ospedale 72, 09124 Cagliari, ITALIA, 2010-2011.
3. Noel A. Childress, Inversion with Respect to the Central Conics, Mathematics Magazine Vol. 38, No. 3 (May, 1965), pp. 147-149.
4. Hamza Khelif, Le jardin des courbes, Dictionnaire raisonné des courbes planes célèbres et remarquables, 2e édition (Manuscrit de 926 pages prêt pour l’impression).
5. José L. Ramirez, Inversions in an Ellipse, Forum Geometricorum Volume 14 (2014) 107–115.
6. David Wells, The Penguin Dictionary of Curious and Interesting Geometry, PENGUIN BOOKS, 1991.
ÉCRIT PAR
Hamza Khelif
Enseignant de mathématique - El-Oued - Algérie
