Certains historiens nous ont appris à distinguer plusieurs temps selon leurs vitesses d’écoulement. Ainsi, dans sa thèse 2Thèse fixée dans ses grandes lignes en 1939, rédigée en captivité au camp de Lübeck, soutenue en Sorbonne en 1947, publiée pour la première fois en 1949, et republiée plusieurs fois depuis. sur La Méditerranée et le monde méditerranéen à l’époque de Philippe II (il s’agit de Philippe II, roi d’Espagne de 1556 à 1598), Fernand Braudel distingue trois espèces :
- « Une histoire quasi immobile (…), celle de l’homme dans ses rapports avec le milieu qui l’entoure, une histoire lente à couler, à se transformer, faite souvent de retours insistants, de cycles sans cesse recommencés (…), presque hors du temps. »
- « Une histoire lentement rythmée (…), une histoire sociale, celle des groupes et des groupements. »
- « Une histoire traditionnelle, si l’on veut de l’histoire à la dimension non de l’homme, mais de l’individu, l’histoire événementielle (…), une agitation de surface. »
« Ainsi sommes-nous arrivé à une décomposition de l’histoire en plans étagés. Ou, si l’on veut, à la distinction, dans le temps de l’histoire, d’un temps géographique, d’un temps social, d’un temps individuel. » (Citations de la préface à la première édition.)
Pour ceux qu’intéresse l’histoire des idées mathématiques, il est frappant que cette grille de lecture s’applique souvent. Sans chercher à retrouver les trois temps de Braudel, j’en prendrai pour preuve d’abord deux exemples, le premier de temps court et le second de temps long.
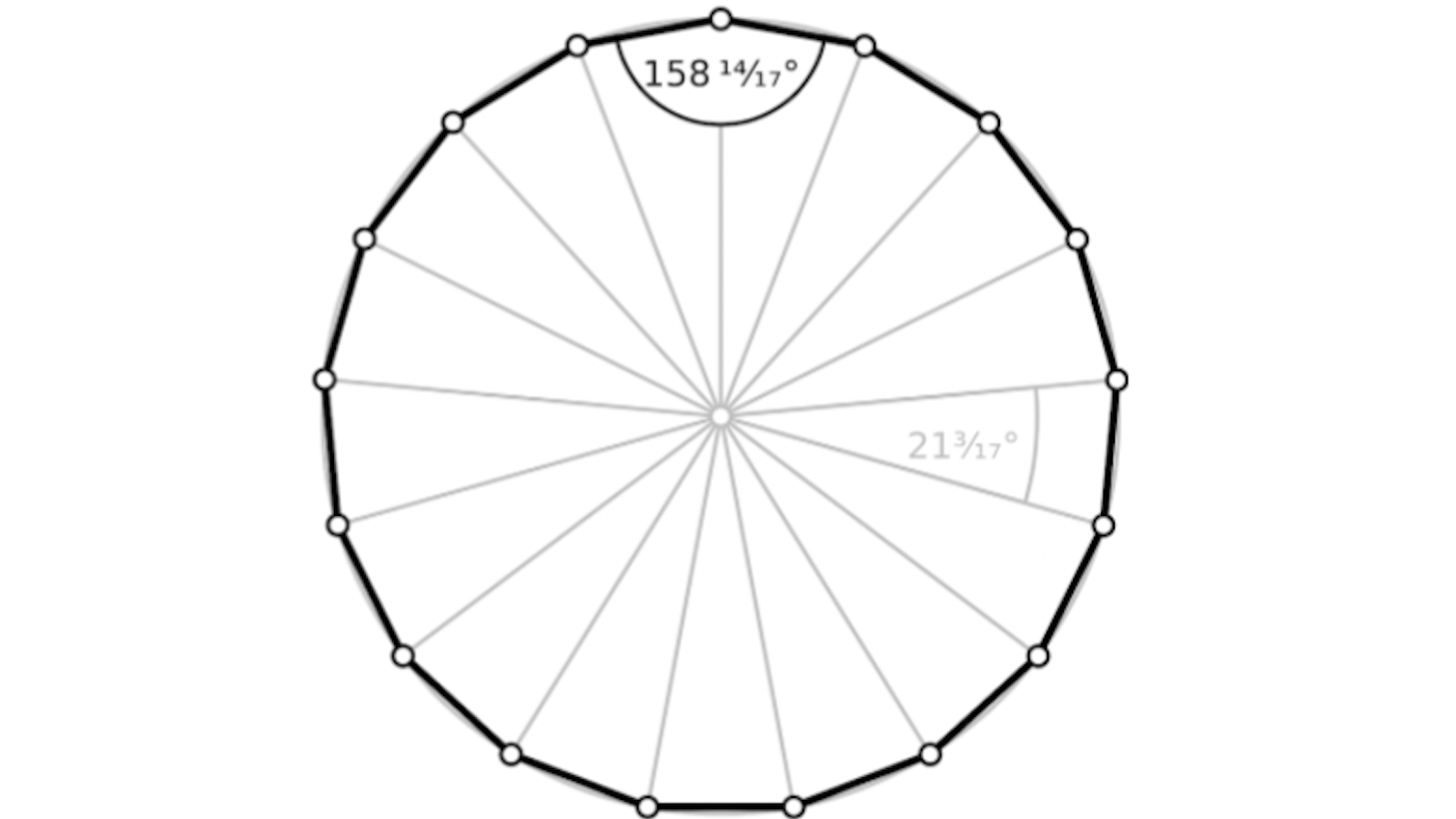
Le 30 mars 1796, Carl Friedrich Gauss découvrit une construction à la règle et au compas d’un polygone régulier à 17 côtés. On connaît la date au jour près, parce que Gauss avait un Mathematisches Tagebuch, une espèce de journal qu’il a tenu de 1796 à 1814, et qui nous est parvenu.
Pour tout entier \(n \ge 3\), un polygone régulier à \(n\) côtés est un polygone dont les \(n\) sommets sont répartis sur un même cercle, à distance exactement égale les uns des autres. Pour en faire un dessin, et plus précisément pour imaginer le principe d’un dessin parfait, les mathématiciens grecs avaient proposé de s’en tenir aux deux instruments rois de la géométrie classique, la règle et le compas. Il est facile de rédiger une suite d’instructions pour construire ainsi un triangle équilatéral (cas \(n = 3\)), un carré (cas \(n=4\)) ou un hexagone (cas \(n=6\))~; c’est un beau résultat d’Euclide (IIIe siècle avant J.-C.) que de décrire la construction d’un pentagone régulier (\(n=5\)). Mais qu’en est-il du cas général ?
Il a fallu attendre 2000 ans pour avoir la réponse. D’abord, Gauss a découvert une construction explicite
pour \(n=17\)~; il avait alors 19 ans, et fut si heureux de cette découverte qu’il décida de consacrer la suite de sa vie (1777-1855) aux mathématiques. Ensuite, pour la majorité des entiers \(n\), par exemple pour \(n=7\), Gauss a montré qu’il est impossible d’obtenir une construction à la règle et au compas d’un polygone régulier à \(n\) côtés.
Pour en revenir à la construction du polygone régulier à \(17\) côtés, c’est donc un exemple parfait de découverte très exactement datable.
Le concept de courbure est utilisé pour modéliser des réalités très diverses : description de l’espace-temps en relativité générale d’Einstein, et structure du graphe sous-jacent à la Toile (ou www, ou web), pour ne citer que deux exemples.
La décantation d’un concept mathématique à la fois général et précis pour rendre compte de la notion de courbure a pris des siècles. Parmi les étapes du développement, on peut citer Issac Newton, qui a défini dans un travail de 1665 ce qu’est la courbure en un point d’une courbe plane, des contributions de Leonard Euler (1707-1783), une avancée importante de Gauss (1777-1855) concernant la courbure en un point d’une surface, la définition d’une courbure pour les espaces de toutes dimensions qu’on trouve dans l’habilitation de Riemann (1854), des travaux de la seconde moitié du XXe siècle sur des notions de courbure dans des « espaces métriques » très généraux, et une quantité exponentiellement croissante de travaux contemporains. En particulier, on se contente parfois aujourd’hui de définir et d’exploiter une notion d’espace métrique à courbure négative, sans ajouter que la courbure puisse être mesurée par un nombre négatif précis, et ce point de vue s’est révélé extrêmement fécond.
Ainsi, le concept de courbure date (pour l’instant) de la période 1650-2000.
Il serait facile de multiplier les exemples de découvertes mathématiques datables au moins à l’année près. Il est plus difficile de comprendre la lente gestation des concepts fondamentaux.
Par exemple, j’aimerais en savoir plus sur le ou les concepts de dimension, dont l’élaboration passe sans doute par les coordonnées de Descartes (dans un appendice au Discours de la Méthode de 1637), par la formalisation de Grassmann de l’algèbre linéaire et la classification de Schläfli des polytopes réguliers au milieu du XIXe siècle, par l’habilitation de Riemann (encore elle), par la quatrième dimension aussi bien dans les relativités d’Einstein (1905 et 1915) que dans d’innombrables romans de science-fiction, par les dimensions non entières introduites par Hausdorff dès 1918 et utilisées par Mandelbrot vers 1970 pour décrire les côtes de Bretagne ; et la liste est pour sûr bien loin d’être close.
Et plusieurs autres notions viennent rapidement à l’esprit auxquels il serait sans nul doute instructif de repenser dans cette optique : l’infini, le hasard, la complexité, …
Quels lecteurs voudront bien prendre cela comme une invitation à poursuivre ?
ÉCRIT PAR
Pierre de la Harpe
Professeur - Université de Genève
