Dans le premier billet sur les tickets de transport, nous nous sommes intéressés à certains mathématiciens rencontrés. Dans ce deuxième billet, nous considérons plutôt quelques curiosités mathématiques que l’on peut retrouver sur certains tickets.
Durant l’année mondiale des mathématiques qui a eu lieu en 2000, les transports de Barcelone ont émis une série de tickets illustrés par des démonstrations visuelles de théorèmes.
-
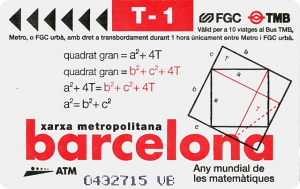
Théorème de Pythagore
-
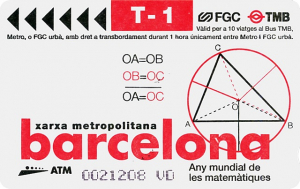
Les médiatrices des côtés d’un triangle se coupent au centre du cercle circonscrit à ce triangle
-
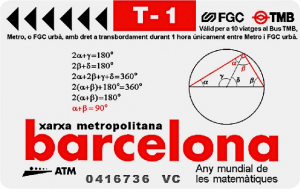
Un triangle dont l’un des côtés est le diamètre du cercle circonscrit est un triangle rectangle
Certaines manifestations mathématiques ont donné lieu à l’émission de tickets personnalisés.
Lors du congrès de l’IFAC (International Federation of Automatic Control) qui s’est tenu à Milan en 2011, l’ATM a émis un ticket spécial destiné aux participants et valable pour la durée du congrès (tirage environ 1 500 ex.).
-
Ticket IFAC
La « Fête de la science » 2014 a donné lieu à l’émission d’un ticket personnalisé valable sur l’ensemble des transports de Moscou (tirage 450 000 ex.).
-
Fête de la Science Moscou
Rien n’empêche également de s’intéresser aux numéros des tickets. Il existe des collections constituées uniquement de tickets dont le numéro possède une particularité numérique. Les Chinois, par exemple, collectionnent les tickets dont le numéro comporte des « 8 » ; dans leur culture ce chiffre est un porte-bonheur. Alors pourquoi ne pas s’intéresser aux palindromes, comme ce ticket de métro de la station Buttes-Chaumont datant de 1912 ou cet abonnement de Concarneau dont le numéro de carte et le numéro de coupon sont tous deux des palindromes ?
-
Palindrome 1
-
Palindrome 2
Les tickets des réseaux étrangers sont également source de ces curiosités mathématiques.
-
Abonnement « handicapé ou retraité » de Tashkent datant de février 2011. Le personnage représenté est le poète et philosophe ouzbek Alisher Navoïy.
-
Abonnement de décembre 2010 du réseau de Tcherepovets.
Bien que cela s’éloigne un peu des mathématiques, n’oublions pas non plus les villes dont le nom est lui-même un palindrome. La plus connue est Laval, il existe deux villes portant ce nom, l’une en Mayenne et l’autre au Canada dans la province de Québec. Ces deux villes possèdent un réseau de transport.
-
Abonnement semestriel de Laval (Mayenne)
-
Abonnement mensuel de Laval (Québec)
En France il existe également Noyon (Oise) qui possède un réseau de transport, mais celui-ci est gratuit et il n’y a malheureusement pas de tickets. Alors, fouillez dans vos boîtes de tickets et vous en trouverez bien quelques-uns dont le numéro possède une particularité amusante. Pour terminer, nous pouvons également nous intéresser aux « références involontaires » que quelques esprits toujours à l’affût arrivent à dénicher. Lorsque la station « Voltaire » ouvrit le 10 décembre 1933 sur la ligne 9 du métro, la CMP pensait sans doute mettre à l’honneur le philosophe du même nom. C’était sans compter sur les aléas de la désignation des guichets : sur les tickets émis par la recette principale apparaît en effet la mention « Pce Voltaire A » qui est un hommage bien involontaire à l’illustre mathématicien italien Vito Volterra (1860-1940).
-
Voltaire ou Volterra?
Un autre mathématicien bien involontairement mis à l’honneur est Bernard Bolzano. Coauteur avec Karl Weierstrass du théorème qui porte leurs noms, il a la chance de porter le nom d’une ville d’Italie, située dans le Tyrol du Sud, ce qui lui vaut d’avoir des tickets à son nom. Chance que n’a pas Karl Weierstrass ; au mieux ce dernier a-t-il peut-être un arrêt de bus dans une ville teutonne.
-
Ticket urbain de Bolzano
-
Abonnement interurbain de Bolzano
Post-scriptum
Pour contacter notre groupe de collectionneurs de tickets :
lebulletinesiteriophile@gmail.com
